EM算法及对GMM的参数估计（EM算法的R实现 vs R mclust包）

最新推荐文章于 2024-05-23 15:24:27 发布

Joyliness

最新推荐文章于 2024-05-23 15:24:27 发布

阅读量1.3w

点赞数 18

本文链接：https://blog.csdn.net/Joyliness/article/details/79504693

版权

EM算法与高斯混合模型（GMM）

EM算法是一种迭代算法，1977年由Dempster等人总结提出，用于含有隐变量（hidden variable）的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由2步组成：

E-step：求期望（expectation）
M-step：最大化（maximization）

所以该算法称为期望极大算法（expectation maximization algorithm），简称EM算法。EM算法的一个重要应用是高斯混合模型（GMM）的参数估计。这里以学习笔记的方式，梳理EM算法在GMM参数估计中的主要过程，记录如下：

【k-mixture GMM的概率分布】

$P (X | Θ) = \sum l = 1 k α l N (X | θ l) = \sum l = 1 k α l N (X | μ l, Σ l)$ $P(X | \Theta) = \sum_{l=1}^k \alpha_l N(X | \theta_l) = \sum_{l=1}^k \alpha_l N(X | \mu_l, \Sigma_l)$

其中， $\Theta = \{ \alpha_1,...,\alpha_k;\theta_1,...,\theta_k\} = \{ \alpha_1,...,\alpha_k;\mu_1,...,\mu_k;\Sigma_1,...,\Sigma_k \}$ ， $\alpha_l$ 代表各高斯的权重， $\sum_{l=1}^k \alpha_l = 1$ 。因此，由 $k$ 个高斯分布分模型组成的GMM可以理解为：这 $k$ 个高斯分布以不同的权重，组合成一个混合模型，混合模型产生的每一个样本点 $x_i$ 都受到 $k$ 个高斯分布的不同影响，影响的大小由权重 $\alpha_l$ 决定。举个不太恰当的例子帮助理解：

$A 、 B 国的混血女 + C 、 D 国的混血男 = 子女 1 + . . . + 子女 n$ $A、B国的混血女 + C、D国的混血男 = 子女_1 + ... + 子女_n$

其中， $A、B、C、D$ 代表4个不同的高斯分布，它们以一定的权重形成一个高斯混合模型，这个模型生出来的每一个 $子女_i$ ，都会受到 $A、B、C、D$ 四国血统的影响，影响的大小由 $A、B、C、D$ 结合时所给出基因多少（权重）决定。
【k-mixture GMM的对数似然函数】

$L (Θ | X) = l o g P (X | Θ) = l o g [\sum l = 1 k α l N (X | μ l, Σ l)] = l o g [\prod i = 1 n \sum l = 1 k α l N (x i | μ l, Σ l)] = \sum I = 1 n [l o g (\sum l = 1 k α l N (x i | μ l, Σ l))]$ $L(\Theta | X) = logP(X | \Theta) = log[\sum_{l=1}^k \alpha_l N(X | \mu_l, \Sigma_l)] = log[\prod_{i=1}^n \sum_{l=1}^k \alpha_l N(x_i | \mu_l, \Sigma_l)] = \sum_{I=1}^n [ log(\sum_{l=1}^k \alpha_l N(x_i | \mu_l, \Sigma_l))]$

我们的目标是求出使 $L(\Theta | X)$ 最大的各个高斯参数，即
$Θ M L E = a r g m a x Θ {l o g P (X | Θ)}$ $\Theta_{MLE} = \mathop{argmax}_{\Theta} \{logP(X | \Theta)\}$ 但是： $log$ 中带有 $\sum$ 符号不利于求导；求导后令其为零也很难得到参数集 $\Theta$ 中的众多参数。
【EM算法的基本思想】

当无法一步到位地将 $\Theta_{MLE}$ 求出来时，可以通过迭代的方式，从初始参数 $\Theta^{(1)}$ $\to$ $\Theta^{(2)}$ $\to$ … $\to$ $\Theta^{(f)}$ ，直到下一次迭代更新，参数的变化十分小，即可认为其收敛，并得到最优参数 $\Theta^{(f)}$ 。

既然是要使对数似然函数最大化，那么每一步迭代都必须保证：

log[P(X|Θ(g+1))]≥log[X|P(Θ(g))]

并且，EM算法给出的关于 $\Theta^{(g+1)}$ 和 $\Theta^{(g)}$ 之间满足的关系是：

Θ(g+1)=argmaxΘ(∫zP(Z|X,Θ(g))logP(X,Z|Θ)dz)

其中， $\Theta^{(g)}$ 是上一次迭代得到的参数， $\Theta^{(g+1)}$ 是下一次迭代更新的参数。 $Z$ 称为隐变量，它是一种不可观测的辅助变量。隐变量的添加必须满足：
1. 加入隐变量后能够简化模型的解法
2. 在概率模型中，加入隐变量后不能改变数据的边缘分布，即要满足 $P(X | \Theta) = \int_z P(X | Z, \Theta) P(Z | \Theta)dz$
3. 【GMM中的隐变量 $Z = \{z_1,z_2,...,z_n\}$ 】
  
  观测数据 $x_i$ （ $i=1,2,...,n$ ）是这样产生的：首先依照各高斯的权重 $\alpha_l$ ，选出第 $l$ 个高斯分布，然后依照第 $l$ 个高斯的概率分布 $N(X | \theta_l)$ 生成观测数据 $x_i$ 。这时观测数据 $x_i$ （ $i=1,2,...,n$ ）是已知的，反映观测数据 $x_i$ 属于哪一个高斯分模型的数据是未知的，将这个未知的、观测不到的数据称为隐变量 $z_i$ （ $i=1,2,...,n$ ）。显然， $z_i\in\{1,2,...,k\}$ 。
  
  $x i \to z i ：样本点 x i 属于第 z i 个高斯分布$ $x_i \to z_i：样本点x_i属于第z_i个高斯分布$
4. 【EM算法的收敛性】
  
  EM算法的核心就是按照 $\Theta^{(g+1)}$ 和 $\Theta^{(g)}$ 之间的等式关系，不断去更新参数，并且能保证每一次更新，都使得对数似然函数逐渐增大。证明EM算法的收敛性：
  
  $P (X | Θ) = P ( X , Z | Θ ) P ( Z | X , Θ )$ $P(X | \Theta) = \frac{P(X,Z | \Theta)}{P(Z | X, \Theta)}$
  
  等式两边取对数并以 $P(Z | X, \Theta^{(g)})$ 为概率分布求期望：
  
  $E [l o g P (X | Θ)] = E [l o g P (X, Z | Θ)] - E [l o g P (Z | X, Θ)]$ $E[logP(X | \Theta)] = E[logP(X,Z | \Theta)] - E[logP(Z |X, \Theta)]$
  
  则等式左边写为：
  
  $\int z P (Z | X, Θ (g)) l o g P (X | Θ) d z = l o g P (X | Θ) \int z P (Z | X, Θ (g)) d z = l o g P (X | Θ)$ $\int_z P(Z | X, \Theta^{(g)})logP(X | \Theta)dz = logP(X | \Theta) \int_z P(Z | X, \Theta^{(g)})dz = logP(X | \Theta)$
  
  等式右边写为：
  
  $\int z P (Z | X, Θ (g)) l o g P (X, Z | Θ) d z - \int z P (Z | X, Θ (g)) l o g P (Z | X, Θ) d z = Q (Θ, Θ (g)) - H (Θ, Θ (g))$ $\int_z P(Z | X, \Theta^{(g)})logP(X,Z | \Theta)dz - \int_z P(Z | X, \Theta^{(g)})logP(Z |X, \Theta)dz = Q(\Theta, \Theta^{(g)}) - H(\Theta, \Theta^{(g)})$
  
  由Jensens不等式可以证明 $H(\Theta^{(g)},\Theta^{(g)}) \ge H(\Theta,\Theta^{(g)})，\forall \Theta$
  
  从而对于任意一次迭代更新参数 $\Theta^{(g+1)}$ ，都有 $H(\Theta^{(g)},\Theta^{(g)}) \ge H(\Theta^{(g+1)},\Theta^{(g)})$
  
  因此，只要 $argmax\{Q(\Theta, \Theta^{(g)})\}$ ，就能保证对数似然函数的最大化。注意 $Q$ 函数中， $\Theta^{(g)}$ 是上一次迭代后得到的固定常数，而 $\Theta$ 是一个变量，作 $argmax$ 不会改变 $\Theta^{(g)}$ 的值。
5. 【EM算法的核心定义：E-step】
  
  上述 $Q(\Theta, \Theta^{(g)})$ 可以看作函数 $logP(X,Z | \Theta)$ 以概率分布 $P(Z | X, \Theta^{(g)})$ 求期望，其定义如下：
  1. 观测值与隐变量的联合概率：
    
    $P (X, Z | Θ) = \prod i = 1 n p (x i, z i | Θ) = \prod i = 1 n p (x i | z i, Θ) p (z i | Θ) = \prod i = 1 n α z i N (x i | μ z i, Σ z i)$ $P(X,Z | \Theta) = \prod_{i=1}^n p(x_i,z_i | \Theta) = \prod_{i=1}^n p(x_i | z_i,\Theta) p(z_i | \Theta) = \prod_{i=1}^n \alpha_{z_i}N(x_i | \mu_{z_i},\Sigma_{z_i})$
  2. 在对应观测值已知的情况下，该观测值来源于哪个高斯的条件概率：
    
    $P (Z | X, Θ (g)) = \prod i = 1 n p (z i | x i, Θ (g)) = \prod i = 1 n α z i N ( x i | μ z i , Σ z i ) \sum k l = 1 α l N ( x i | μ l , Σ l )$ $P(Z | X, \Theta^{(g)}) = \prod_{i=1}^n p(z_i | x_i, \Theta^{(g)}) = \prod_{i=1}^n \frac{\alpha_{z_i} N(x_i | \mu_{z_i},\Sigma_{z_i})}{\sum_{l=1}^k \alpha_l N(x_i | \mu_l,\Sigma_l)}$
6. 【求解 $\Theta^{(g+1)}$ ：M-step】
  
  将上述函数的定义代入 $Q(\Theta, \Theta^{(g)})$ ，求导令其为零，得到 $\Theta^{(g+1)}$ 的值：
  
  $α (g + 1) l = \sum n i = 1 p ( l | x i , Θ ( g ) ) n$ $\alpha_l^{(g+1)} = \frac{\sum_{i=1}^n p(l | x_i,\Theta^{(g)})}{n}$
  
  $μ (g + 1) l = \sum n i = 1 x i p ( l | x i , Θ ( g ) ) \sum n i = 1 p ( l | x i , Θ ( g ) )$ $\mu_l^{(g+1)} = \frac{\sum_{i=1}^n x_i p(l | x_i,\Theta^{(g)})}{\sum_{i=1}^n p(l | x_i,\Theta^{(g)})}$
  
  $Σ (g + 1) l = \sum n i = 1 [ x i - μ ( i + 1 ) l ] [ x i - μ ( i + 1 ) l ] T p ( l | x i , Θ ( g ) ) \sum n i = 1 p ( l | x i , Θ ( g ) )$ $\Sigma_l^{(g+1)} = \frac{\sum_{i=1}^n [x_i - \mu_l^{(i+1)}] [x_i - \mu_l^{(i+1)}]^T p(l | x_i,\Theta^{(g)})}{\sum_{i=1}^n p(l | x_i,\Theta^{(g)})}$
  
  其中， $p(l | x_i,\Theta^{(g)})$ 称为responsibility probability，它是指当得到样本点 $x_i$ 后，该样本点属于第 $l$ 个高斯分布的概率。

GMM参数估计示例

【模拟样本】指定2个高斯分布的参数，并令其以0.4和0.6的权重随机生成5000个样本

# 生成n=5000的样本samp
set.seed(637351)
n <- 5000

# 权重0.4，高斯参数N(3，1)
alpha1 <- 0.4
miu1   <- 3
sigma1 <- 1

# 权重0.6，高斯参数N(-2，4)
alpha2 <- 0.6
miu2   <- -2
sigma2 <- 2

n1 <- floor(n*alpha1)
n2 <- n-n1

samp <-numeric(n)
samp[1:n1] <- rnorm(n1, miu1, sigma1)
samp[(n1+1):n] <- rnorm(n2, miu2, sigma2)

# 高斯混合模型的密度函数图
hist(samp, freq = FALSE)
lines(density(samp), col = 'red')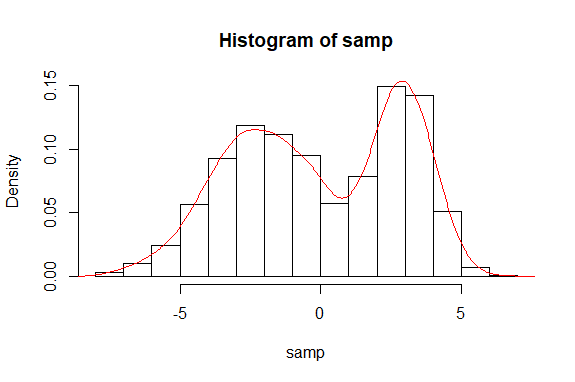

EM算法的R实现

【EM求解】现在假设手里只有样本samp，已知其来自2个高斯分布（可以分成2类），但各高斯的参数和权重未知，用EM算法求解：

# 设定高斯分布的个数，准备空矩阵
k <- 2
prob <- matrix(rep(0, k*n), nrow = n)
weight <- matrix(rep(0, k*n), nrow = n)

# 初始权重alpha平均分配，高斯参数miu、sigma由均匀分布随机产生
alpha <- c(0.5, 0.5)
miu   <- runif(k)
sigma <- runif(k)

# EM算法实现
for (step in 1:200) {
  # E-step：求第i个样本来自第j个高斯的概率
  for (j in 1:k) {
    prob[, j]   <- sapply(samp, dnorm, miu[j], sigma[j])
    weight[, j] <- alpha[j] * prob[, j]
  }
  row_sum <- rowSums(weight)
  prob    <- weight/row_sum

  # 记录上一次迭代的参数
  oldalpha <- alpha
  oldmiu   <- miu
  oldsigma <- sigma

  # M-step：最大化是通过求导令其为零的方法，这里直接给出参数优化结果
  for (j in 1:k) {
    sum1     <- sum(prob[, j])
    sum2     <- sum(samp*prob[, j])
    alpha[j] <- sum1/n
    miu[j]   <- sum2/sum1
    sum3     <- sum(prob[, j]*(samp-miu[j])^2)
    sigma[j] <- sqrt(sum3/sum1)
  }

  # 设阈值：当上一步迭代得到的参数与下一步迭代得到的参数变化很小，即认为收敛
  threshold <- 1e-5
  if (sum(abs(alpha - oldalpha)) < threshold & 
      sum(abs(miu - oldmiu))     < threshold & 
      sum(abs(sigma - oldsigma)) < threshold) break
  cat('step', step, 'alpha', alpha, 'miu', miu, 'sigma', sigma, '\n')
}

【迭代结果】省略部分迭代过程，经125次迭代后，得到最优参数：权重为 $0.402$ 的高斯 $N(2.98，0.96^2)$ ，权重为 $0.598$ 的高斯 $N(-2.05，1.95^2)$ 。

step 1 alpha 0.9276533 0.07234668 miu -0.02635882 -0.06741285 sigma 3.062992 0.6167386 
step 2 alpha 0.9616189 0.03838105 miu -0.02227273 -0.2061188 sigma 3.010045 0.664219 
step 3 alpha 0.9771787 0.02282128 miu -0.02167226 -0.3571784 sigma 2.986799 0.6915781 
step 4 alpha 0.9853229 0.0146771 miu -0.02206765 -0.5168036 sigma 2.97487 0.7053047 
step 5 alpha 0.9899198 0.01008019 miu -0.02270511 -0.6798185 sigma 2.968202 0.7097974 
step 6 alpha 0.9926533 0.007346716 miu -0.02331694 -0.8416411 sigma 2.96425 0.7089913 
step 7 alpha 0.9943434 0.005656624 miu -0.02380939 -0.9995759 sigma 2.961799 0.7057652 
step 8 alpha 0.9954167 0.004583325 miu -0.0241567 -1.152648 sigma 2.96022 0.7015791 
step 9 alpha 0.9961051 0.003894859 miu -0.02435778 -1.300695 sigma 2.959172 0.6968685 
step 10 alpha 0.9965391 0.003460889 miu -0.02441699 -1.443691 sigma 2.958461 0.6916394 
...
step 120 alpha 0.4016976 0.5983024 miu 2.982002 -2.051124 sigma 0.9602173 1.948754 
step 121 alpha 0.4016951 0.5983049 miu 2.98201 -2.051108 sigma 0.9602116 1.948766 
step 122 alpha 0.401693 0.598307 miu 2.982017 -2.051095 sigma 0.9602069 1.948776 
step 123 alpha 0.4016913 0.5983087 miu 2.982022 -2.051084 sigma 0.9602031 1.948785 
step 124 alpha 0.4016899 0.5983101 miu 2.982027 -2.051075 sigma 0.9602 1.948791 
step 125 alpha 0.4016888 0.5983112 miu 2.98203 -2.051068 sigma 0.9601974 1.948797

【GMM聚类】现在已经得到2个高斯分布的权重和参数，因此可以对样本进行归类，亦即将得到的参数在E-step重新计算一遍：

prob1    <- dnorm(samp, miu[1], sigma[1])
prob2    <- dnorm(samp, miu[2], sigma[2])
sum_prob <- alpha[1]*prob1+alpha[2]*prob2

# 第i个样本来自第1个高斯的概率
weight1 <- (alpha[1]*prob1)/sum_prob

# 第i个样本来自第2个高斯的概率
weight2 <- (alpha[2]*prob2)/sum_prob

# 比较样本点来自第1、2个高斯的概率，哪个概率大归入哪一类
z <- ifelse(weight1 > weight2, 1, 2)

# z的计算也可以用如下for循环
for (i in 1:n) {
  if (weight1[i] > weight2[i]) {
    z[i] <- 1
  } else if (weight1[i] < weight2[i]) {
    z[i] <- 2
  } else {
    z[i] <- 0
  }
}
# 查看归入1、2类的样本个数
table(z)

【聚类结果】属于第1类的样本点有2081个，占 $\frac{2081}{5000}=0.4162$ ；属于第2类的样本点有2919个，占 $\frac{2919}{5000}=0.5838$ 。

z
   1    2 
2081 2919

【代码理解】在【EM算法求解】、【GMM聚类】步骤中的部分代码计算，可以理解如下：

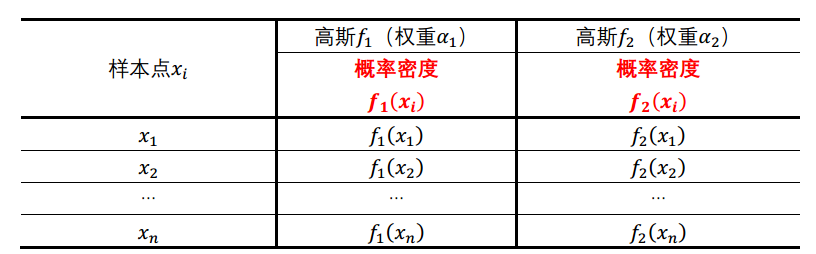
# 【EM求解】对应代码
prob[, j] <- sapply(samp, dnorm, miu[j], sigma[j])
# 【GMM聚类】对应代码
prob1 <- dnorm(samp, miu[1], sigma[1])
prob2 <- dnorm(samp, miu[2], sigma[2])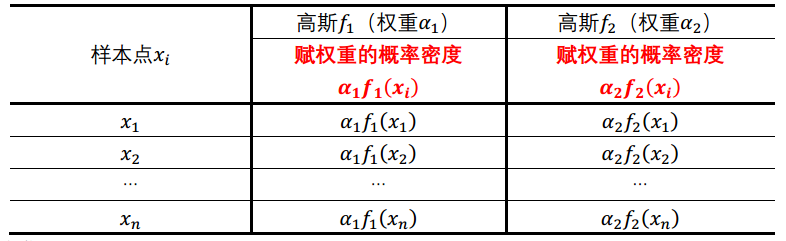

# 【EM求解】对应代码
weight[, j] <- alpha[j] * prob[, j]

# 【EM求解】对应代码
row_sum <- rowSums(weight)
# 【GMM聚类】对应代码
sum_prob <- alpha[1]*prob1+alpha[2]*prob2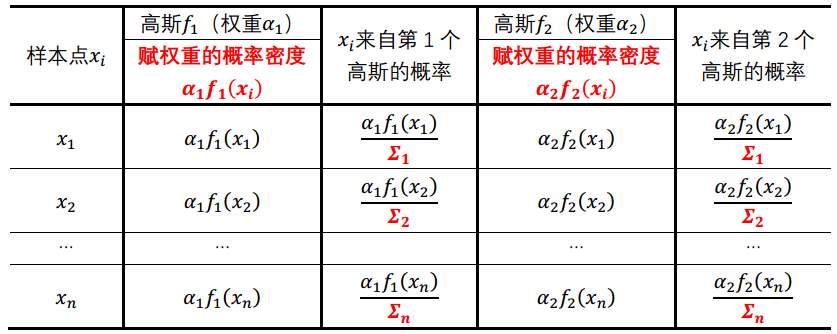

# 【EM求解】对应代码
prob <- weight/row_sum
# 【GMM聚类】对应代码
weight1 <- (alpha[1]*prob1)/sum_prob
weight2 <- (alpha[2]*prob2)/sum_prob

R mclust包

mclust包提供了利用GMM对数据进行聚类分析的方法。其中函数Mclust()是进行EM聚类的核心函数，它的基本调用格式为：

Mclust(data, G = NULL, modelNames = NULL, prior = NULL, 
       control = emControl(), initialization = NULL, 
       warn = mclust.options("warn"), ...)

其中，data是待处理数据集；G为预设类别数，默认值为1至9，即由软件根据BIC的值在1-9中选择最优值。下面直接用mclust包的函数对生成samp的GMM进行估计：

library(mclust)
em <- Mclust(samp)
summary(em, parameters = T)

【估计结果】得到的最优参数：权重为 $0.405$ 的高斯 $N(2.97，0.94)$ ，权重为 $0.595$ 的高斯 $N(-2.07，3.74)$ 。

----------------------------------------------------
Gaussian finite mixture model fitted by EM algorithm 
----------------------------------------------------

Mclust V (univariate, unequal variance) model with 2 components:

 log.likelihood    n df       BIC       ICL
       -11817.8 5000  5 -23678.18 -24140.79

Clustering table:
   1    2 
2910 2090 

Mixing probabilities:
        1         2 
0.5950857 0.4049143 

Means:
        1         2 
-2.071201  2.971525 

Variances:
        1         2 
3.7377492 0.9364023

参考资料：
统计学习方法
 EM算法的R实现和高斯混合模型
 R语言实战：机器学习与数据分析
 Package ‘mclust’
聚类(1)——混合高斯模型 Gaussian Mixture Model

Joyliness

关注

18
点赞
踩
148

收藏

觉得还不错? 一键收藏
4
评论
EM算法及对GMM的参数估计（EM算法的R实现 vs R mclust包）

EM算法与高斯混合模型（GMM）EM算法是一种迭代算法，1977年由Dempster等人总结提出，用于含有隐变量（hidden variable）的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由2步组成：E-step：求期望（expectation）M-step：最大化（maximization）所以该算法称为期望极大算法（expectation maxim...
复制链接

扫一扫