统计检验中的两类错误
在进行假设检验时,分别提出原假设(Null Hypothesis)和备择假设(Alternative Hypothesis),检验结果可能出现的两类错误:
- 原假设实际上是正确的,而检验结果却拒绝原假设,称为
第一类/第一型错误(Type I error)、弃真错误 - 原假设实际上是错误的,而检验结果却接受原假设,称为
第二类/第二型错误(Type II error)、取伪错误
ROC Curve
- 起源与发展
ROC曲线(Receiver Operating Characteristic Curve),又称为感受性曲线(Sensitivity Curve),是一种坐标图式的分析工具。它首先是由二战中的电子工程师和雷达工程师发明的,用来侦测战场上的敌军载具(飞机、船舰),即信号检测理论。之后很快就被引入了心理学来进行信号的知觉检测。数十年来,ROC分析被用于医学、无线电、生物学、犯罪心理学领域中,最近在机器学习和数据挖掘领域也得到了很好的发展。
- 用途
ROC曲线用于衡量二元分类模型的优劣,也就是说,它所衡量的模型,一定只有两个判断结果(非黑即白):阳性/阴性、得病/不得病、违约/不违约、敌军/非敌军、正例/负例…等,通常将这两种结果分别记为1和0。
例如,有一个模型,可以用来判断人体是否得病。现将五个身体状况分别为健康(0)、得病(1)、健康(0)、健康(0)、得病(1)的样本的各项生理指标输入该模型,并假设模型输出的五个人的得病概率分别为0.30,0.60,0.55,0.40,0.50。注意,在做ROC曲线分析时,输入模型的待判别样本全部是已知真值的,如上例的样本,已知其是健康、得病、健康、健康、得病。
那么,得到这五个概率后,模型又是怎样进一步判别他们是否得病的?首先抛开我们传统的0.50认知,这里并不是概率大于0.50就认为该样本得病了。因为模型准确性本身就是待验证的,其得到的预测结果当然也不是百分之百正确,这时候就需要医生结合从业经验,人为给定一个阈值(threshold),也称为cut-off point。只有当样本的预测概率大于阈值时,才将该样本归为得病。
显然,如果阈值过低(判为得病的条件宽松,得病门槛低),就容易将健康样本误判为得病;如果阈值过高(判为得病的条件严谨,得病门槛高),就容易漏掉真正的得病样本,使一部分得病样本误判为健康。为了帮助理解,我们将分类模型视为一个筛网,阈值高低视为筛网孔的尺寸,健康样本为大沙粒,得病样本为小沙粒,则通过筛网的,应该是得病样本;而留在筛网上的,应该是健康样本。那么:
- 阈值过低 = 判为得病的条件宽松 = 筛网孔过大 = 大沙粒(健康样本)也不小心通过筛网(误判为得病)
- 阈值过高 = 判为得病的条件严谨 = 筛网孔过小 = 小沙粒(得病样本)过不去,滞留在筛网(误判为健康)
由此可见,只有选定阈值以后,才能把模型预测概率转化为具体的类别,而不同的阈值对模型的判别效果有很大的影响。阈值虽然不能穷举(其取值从0-1),但取不同的阈值,对模型分类结果的影响却是可以罗列出来的。结合上面的例子,可以设定如下6个范围的阈值,并得到如下6种不同的分类结果。可以看到,阈值过低时,模型将所有样本都判为得病;阈值过高时,模型将所有样本都判为健康:
| 阈值t的范围 | 预测结果 |
|---|---|
| 0 ≤ \le ≤ t < \lt < 0.30 | (得病,得病,得病,得病,得病)记为(1,1,1,1,1) |
| 0.30 ≤ \le ≤ t < \lt < 0.40 | (健康,得病,得病,得病,得病)记为(0,1,1,1,1) |
| 0.40 ≤ \le ≤ t < \lt < 0.50 | (健康,得病,得病,健康,得病)记为(0,1,1,0,1) |
| 0.50 ≤ \le ≤ t < \lt < 0.55 | (健康,得病,得病,健康,健康)记为(0,1,1,0,0) |
| 0.55 ≤ \le ≤ t < \lt < 0.60 | (健康,得病,健康,健康,健康)记为(0,1,0,0,0) |
| t ≥ \ge ≥ 0.60 | (健康,健康,健康,健康,健康)记为(0,0,0,0,0) |
- 定义
以上通过实例,对ROC曲线所衡量的模型进行了简单解释。回到ROC曲线本身,既然是呈现在坐标图上的曲线,则一定有横、纵坐标两个变量。而且ROC曲线是衡量模型优劣,必然要对模型的分类结果进行统计分析,因此RCO曲线分析的基础,就是上述表格中的数据。
显然,6个分类结果对比真实情况,各有差异。这时候,我们最想了解的应该是:该模型判别的正确率有多高?事实上,判断结果一定是如下情况之一:
- 得病样本被正确判断为得病样本(
真阳性TP) - 得病样本被误判为健康样本(
伪阴性FN) - 健康样本被正确判断为健康样本(
真阴性TN) - 健康样本被误判为得病样本(
伪阳性FP)
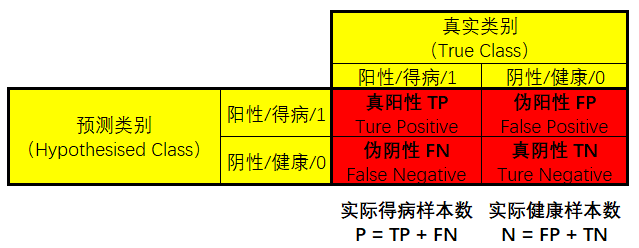
在医学统计中,假设检验的原假设是样本健康,备择假设是样本得病。那么,伪阳性FP的情况是:明明健康,却判其得病,是对得病的错误肯定,拒绝了正确的原假设,属于弃真错误。
而伪阴性FN的情况是:明明得病,却判其健康,是对得病的错误否定,接受了错误的原假设,属于取伪错误。
从而可以引入一系列常见的性能指标:
TPR(True Positive Rate)= T P T P + F N \frac{TP}{TP + FN} TP+FNTP = T P P \frac{TP}{P} PTP ,称为真阳性率
又可称命中率(Hit Rate)、敏感度(Sensitivity)FPR(False Positive Rate)= F P F P + T N \frac{FP}{FP + TN} FP+TNFP = F P N \frac{FP}{N} NFP ,称为伪阳性率
又可称错误命中率/假警报率(False Alarm Rate)TNR(True Negative Rate)= T N F P + T N \frac{TN}{FP + TN} FP+TNTN = T N N \frac{TN}{N} NTN = 1 − F P R 1 - FPR 1−FPR,称为真阴性率
又可称特异度(Specificity)Recall=TPR= T P T P + F N \frac{TP}{TP + FN} TP+FNTP = T P P \frac{TP}{P} PTP,称为召回率Precision= T P T P + F P \frac{TP}{TP + FP} TP+FPTP,称为精确率ACC(Accuracy)= T P + T N P + N \frac{TP + TN}{P + N} P+NTP+TN,称为准确度F-measure= 2 1 P r e c i s i o n + 1 R e c a l l \frac{2}{\frac{1}{Precision} + \frac{1}{Recall}} Precision1+Recall12 = 2 T P 2 T P + F P + F N \frac{2TP}{2TP + FP+ FN} 2TP+FP+FN2TP,称为F1值/F1评分
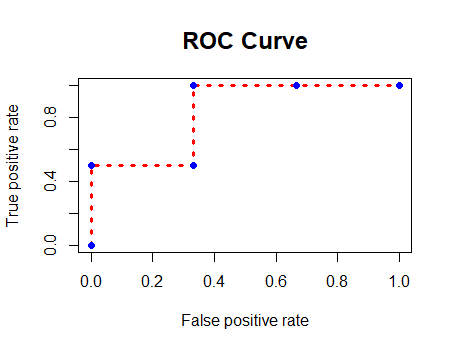
所以,ROC曲线是以FPR为横坐标、以TPR为纵坐标所形成的曲线,其坐标点为(FPR,TPR)。注意,工程上一般不采用FPR、TPR这两个术语,而是分别用1-Specificity、Sensitivity来代替,则ROC曲线上的坐标点为(1-Specificity,Sensitivity)。依旧沿用上述例子,模型根据不同的阈值,每得到一个预测结果,就可以与真值(0,1,0,0,1)做一次对比,并计算出一个坐标点(FPR,TPR)。因此,上述例子的ROC曲线有6个坐标点,手动计算并用R语言作图验证如下:
| 阈值t的范围 | 预测结果 | 指标值 | (FPR,TPR) |
|---|---|---|---|
| 0 ≤ \le ≤ t < \lt < 0.30 | (1,1,1,1,1) | FP = 3,TN = 0,TP = 2,FN = 0 | (1,1) |
| 0.30 ≤ \le ≤ t < \lt < 0.40 | (0,1,1,1,1) | FP = 2,TN = 1,TP = 2,FN = 0 | ( 2 3 \frac{2}{3} 32,1) |
| 0.40 ≤ \le ≤ t < \lt < 0.50 | (0,1,1,0,1) | FP = 1,TN = 2,TP = 2,FN = 0 | ( 1 3 \frac{1}{3} 31,1) |
| 0.50 ≤ \le ≤ t < \lt < 0.55 | (0,1,1,0,0) | FP = 1,TN = 2,TP = 1,FN = 1 | ( 1 3 \frac{1}{3} 31, 1 2 \frac{1}{2} 21) |
| 0.55 ≤ \le ≤ t < \lt < 0.60 | (0,1,0,0,0) | FP = 0,TN = 3,TP = 1,FN = 1 | (0, 1 2 \frac{1}{2} 21) |
| t ≥ \ge ≥ 0.60 | (0,0,0,0,0) | FP = 0,TN = 3,TP = 0,FN = 2 | (0,0) |
> library(ROCR)
> predictions <- c(0.30, 0.60, 0.55, 0.40, 0.50)
> labels <- c(0, 1, 0, 0, 1)
> pred <- prediction(predictions = predictions, labels = labels)
> # 参数predictions是模型的预测概率,参数labels是样本的真实类别
> pred
An object of class "prediction"
Slot "predictions":
[[1]]
[1] 0.30 0.60 0.55 0.40 0.50
Slot "labels":
[[1]]
[1] 0 1 0 0 1
Levels: 0 < 1
Slot "cutoffs":
[[1]]
[1] Inf 0.60 0.55 0.50 0.40 0.30
Slot "fp":
[[1]]
[1] 0 0 1 1 2 3
Slot "tp":
[[1]]
[1] 0 1 1 2 2 2
Slot "tn":
[[1]]
[1] 3 3 2 2 1 0
Slot "fn":
[[1]]
[1] 2 1 1 0 0 0
Slot "n.pos":
[[1]]
[1] 2
Slot "n.neg":
[[1]]
[1] 3
Slot "n.pos.pred":
[[1]]
[1] 0 1 2 3 4 5
Slot "n.neg.pred":
[[1]]
[1] 5 4 3 2 1 0
> perf <- performance(prediction.obj = pred, measure = "tpr", x.measure = "fpr")
> # 参数prediction.obj是正在做分类预测的样本对象
> # 参数measure指定第一种性能测量方法,参数x.measure指定第二种性能测量方法
> perf
An object of class "performance"
Slot "x.name":
[1] "False positive rate"
Slot "y.name":
[1] "True positive rate"
Slot "alpha.name":
[1] "Cutoff"
Slot "x.values":
[[1]]
[1] 0.0000000 0.0000000 0.3333333 0.3333333 0.6666667 1.0000000
Slot "y.values":
[[1]]
[1] 0.0 0.5 0.5 1.0 1.0 1.0
Slot "alpha.values":
[[1]]
[1] Inf 0.60 0.55 0.50 0.40 0.30
> plot(perf, col = "red", lty = 3, lwd = 3, cex.lab = 1, cex.axis = 1,
cex.main = 1.5, main = "ROC Curve")
> # 画出ROC曲线
> points(unlist(perf@x.values), unlist(perf@y.values), pch = 19, col = "blue")
> # 标上坐标点
- ROC空间与Baseline
考察ROC空间的四个点:(1,1),(0,0),(0,1),(1,0)。
在(1,1)处,FPR = 1,TPR = 1。说明TN = 0,FN = 0。分类器将所有样本都判为阳性/得病/1。
在(0,0)处,FPR = 0,TPR = 0。说明FP = 0,TP = 0,分类器将所有样本都判为阴性/健康/0。
在(0,1)处,FPR = 0,TPR = 1。说明FP = 0,FN = 0,分类器将所有样本都分对了(最佳)。
在(1,0)处,FPR = 1,TPR = 0。说明TN = 0,TP = 0,分类器将所有样本都分错了(最差)。
最佳分类器在点(0,1)处取得,说明ROC空间左上角的点代表分类器效果更好。
考察直线:TPR = FPR。
这是ROC空间的对角线,其上各点满足
T
P
P
\frac{TP}{P}
PTP =
F
P
N
\frac{FP}{N}
NFP,它表示的是一个采用随机猜测策略的分类器的结果。如何理解随机猜测策略分类器?现在重新抽取真实样本100个,其中40个得病,60个健康,即:
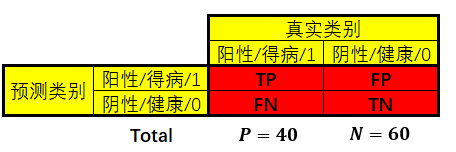
那么从中随机抽取1个样本,拿到得病样本的概率应该是 40 40 + 60 \frac{40}{40 + 60} 40+6040 = 2 5 \frac{2}{5} 52。现在有一个采取随机分类策略的模型,对这100个样本进行分类,其中 t t t个归为阳性, 100 − t 100-t 100−t个归为阴性,即:
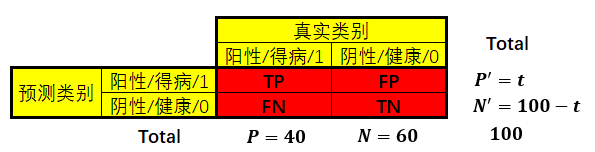
由于是随机分类,被模型判为阳性的 t t t个样本,理论上应该和总体样本的阳性、阴性概率相同,即t个样本中有 2 5 t \frac{2}{5}t 52t得病, 3 5 t \frac{3}{5}t 53t健康:
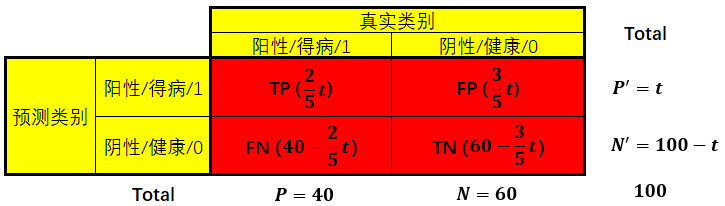
在这种情况下,不论
t
t
t取何值,即随机模型不论判别出多少个阳性、阴性样本,始终满足
T
P
F
P
\frac{TP}{FP}
FPTP =
P
N
\frac{P}{N}
NP,变形即得对角线上任意一点满足的等式关系:
T
P
P
\frac{TP}{P}
PTP =
F
P
N
\frac{FP}{N}
NFP。在(0.5,0.5)处,TP = FN,FP = TN,分类器随机将一半样本判为阳性,另一半样本判为阴性。
TPR = FPR可以视为一条Baseline,一个模型要有所提升,首先就应该比这个Baseline表现要好。如果模型的分类结果比随机分类效果还差,真真有点狗带。ROC曲线就是用来评估当前模型比随机分类效果更强的程度(肯定是比Baseline强,主要考察的是强多少),ROC曲线与Baseline偏离越大(越靠近左上角),模型的分类效果就越好。ROC曲线一般呈现阶梯上升状,当阈值的取值类别越多,ROC曲线的取值点越多,曲线就越平滑。
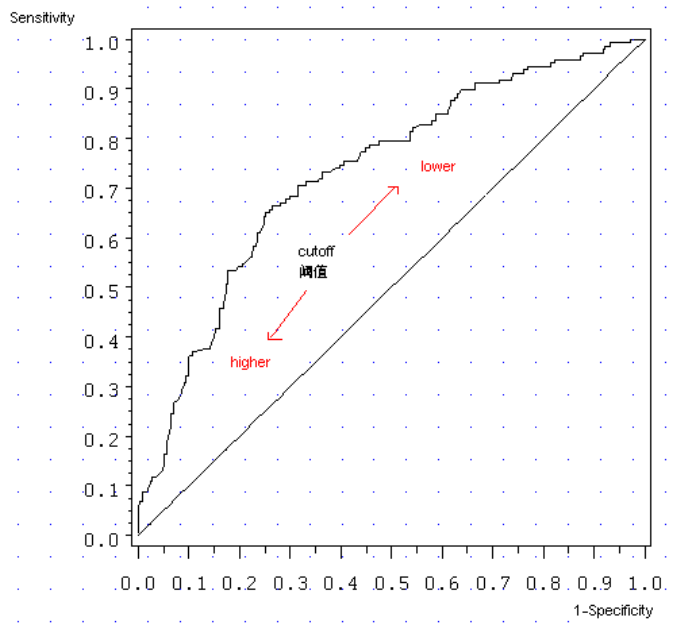
图片来自分类模型的性能评估——以 SAS Logistic 回归为例 (2): ROC 和 AUC
AUC
- 定义
AUC(Area Under Curve)是最常见的、用于表述一条ROC曲线的统计量,它被定义为ROC曲线下方与横轴围成的面积,显然这个面积的数值不会大于1。由于ROC曲线一般都处于TPR = FPR的上方,所以AUC的取值范围在0.5-1之间。
使用AUC值作为评价标准,是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好。每一条ROC曲线代表一个分类模型,各曲线上的每一个点代表不同阈值下的分类结果。当不同的ROC曲线相互交叉时,便难以判别模型的优劣。而作为一个数值,AUC值越大,可以直观地说明分类器效果更好。
在上一节的例子中,观察ROC曲线图可以直接计算AUC值为
5
6
\frac{5}{6}
65,同样可以用R语言计算:
> library(dplyr)
> auc <- performance(pred, 'auc') %>% .@y.values %>% unlist()
> auc
[1] 0.8333333
Mann–Whitney U test and statistic
- 关系
从定义上看,AUC衡量的是ROC曲线下与横轴围成的面积值。但从统计角度来理解AUC的意义,还需要结合Mann–Whitney U统计量。
首先,AUC与Mann-Whitney U统计量基本上是等价的:
A
U
C
=
U
n
1
n
0
AUC = \frac{U}{n_1n_0}
AUC=n1n0U
其中,
n
1
n_1
n1和
n
0
n_0
n0分表代表真实样本中,样本1的总个数和样本0的总个数。则上例中
n
0
=
3
n_0=3
n0=3,
n
1
=
2
n_1=2
n1=2。且由于
A
U
C
=
5
6
AUC=\frac{5}{6}
AUC=65,因此
U
=
5
U=5
U=5。这是从二者的关系式得到的U统计量的值,下面从U统计量的定义来计算,验证二者的关系。
- 起源与发展
在统计分析方法中,通常有参数统计方法和非参数统计方法。
- 当总体的分布形式已知,而其中的某些参数未知时,通常是从总体中随机抽取样本,根据样本信息对总体参数(如均值、方差等)进行估计或假设检验,即
参数统计方法。 - 而在许多实际问题中,总体分布的具体形式大多是未知或知之甚少的,也不能对总体的分布形式作进一步的假定(如假定总体为近似正态分布等),只能确定总体是连续分布还是离散分布,此时利用样本数据对总体分布形态进行推断,不涉及有关总体分布的参数,故称为
非参数统计方法,基于秩次的统计方法是非参数统计方法中的一种。
进一步地,在非参数统计方法中,单、双样本的检验方法主要经历了如下发展:
Sign test(符号检验)
⇒
\Rightarrow
⇒ Wilcoxon Signed-rank test(威尔科克森符号秩检验)
⇒
\Rightarrow
⇒ Mann–Whitney U test(曼–惠特尼U检验)
这里只对上述检验方法的基本思想作简单介绍:
Sign test(符号检验)是最简单的非参数检验方法,它是根据
+
+
+、
−
-
−号的个数,来检验单样本或配对样本的特征。若两个样本差异不显著,则
+
+
+、
−
-
−号的个数应大致各占一半。有时当配对比较的结果只能定性的表示,如试验前后比较结果为颜色从深变浅、程度从强变弱,成绩从一般变优秀,即不能获得具体数字,就应该用符号检验,例如用
+
+
+表示颜色从浅变深,用
−
-
−表示颜色从深变浅。
例1.(单样本的检验)从10个商场,收集某一品牌洗碗机的价格,得到10个样本数据,现给定一个行业价,将样本中大于行业价的记为
+
+
+,小于行业价的记为
−
-
−,检验这10个样本数据与行业价是否有显著差异;
例2.(配对样本的检验)有10位受试者,服用某款镇静剂,服药后,精神状态维持亢奋的样本记为
+
+
+,精神状态得到安抚的样本记为
−
-
−,检验镇静剂是否有效;
Wilcoxon Signed-rank test(威尔科克森符号秩检验)是由Wilcoxon于1945年提出的。它是在符号检验的基础上发展起来的,其优点在于:在两组配对资料的差异有具体数值的情况下,符号检验只利用大于0和小于0的信息(即
+
+
+和
−
-
−的信息),而对差异大小所包含的信息却未加利用,但Wilcoxon符号秩检验方法既考虑了正、负号,又利用了差值大小,故效率较符号检验法高。该方法不要求成对数据的差值服从正态分布,只要求对称分布即可,可检验成对观测数据之差是否来自均值为0的总体。
例3.(配对样本的检验)有10位受试者,服用某款减肥药,将服药后的体重减去服药前的体重,得到10个差值
d
i
f
dif
dif(有正有负);将
a
b
s
∣
d
i
f
∣
abs|dif|
abs∣dif∣排序求秩,计算统计量:正
d
i
f
dif
dif的秩和
W
+
W^+
W+、负
d
i
f
dif
dif的秩和
W
−
W^-
W−,检验减肥药是否有效;
威尔科克森符号秩检验主要是针对两样本量相同的情况。在此基础上,1947年,Mann和Whitney又在考虑到不等样本的情况下补充了Mann–Whitney U test(曼–惠特尼U检验),又称为Mann–Whitney–Wilcoxon(MWW)检验、Wilcoxon–Mann–Whitney(WMW)检验、Wilcoxon rank-sum test(Wilcoxon秩和检验)。
- 从定义上理解检验过程
Mann–Whitney U test:记两个独立的连续型随机变量总体
X
X
X和
Y
Y
Y的样本分别为
x
1
,
.
.
.
,
x
m
x_1,...,x_m
x1,...,xm,
y
1
,
.
.
.
,
y
n
y_1,...,y_n
y1,...,yn。样本总容量为
m
+
n
m+n
m+n,考虑所有样本值之间互不相等、即没有结点的情况。假设总体
X
X
X和
Y
Y
Y除了总体均值以外,其他完全相同。两个总体的分布有类似形状,无需假定对称。目的是检验这两个总体的均值
μ
X
\mu_X
μX、
μ
Y
\mu_Y
μY是否有显著的差别。则原假设和备择假设分别为:
H
0
:
μ
X
=
μ
Y
H_0:\mu_X=\mu_Y
H0:μX=μY
H
1
:
μ
X
≠
μ
Y
H_1:\mu_X\neq\mu_Y
H1:μX=μY
-
Wilcoxon秩和统计量:将样本 x 1 , . . . , x m x_1,...,x_m x1,...,xm和 y 1 , . . . , y n y_1,...,y_n y1,...,yn混合在一起,将 m + n m+n m+n个数按照从小到大顺序排列起来并求秩,计算样本 X X X的观测值的秩和 W X W_X WX、样本 Y Y Y的观测值的秩和 W Y W_Y WY,称 W X W_X WX或 W Y W_Y WY为Wilcoxon秩和统计量。显然,如果秩和 W X W_X WX过小,说明样本 X X X的观测值在排序时,普遍靠前,则总体 X X X的均值很有可能小于总体 Y Y Y的均值,有理由怀疑甚至拒绝原假设。对于 W Y W_Y WY也是同理。此外,所有秩和满足:
W X + W Y = ( m + n ) ( m + n + 1 ) 2 W_X+W_Y=\frac{(m+n)(m+n+1)}{2} WX+WY=2(m+n)(m+n+1) -
Mann-Whitney U统计量(定义法):记样本集 I m = { x 1 , . . . , x m } I_m=\{x_1,...,x_m\} Im={x1,...,xm}, I n = { y 1 , . . . , y n } I_n=\{y_1,...,y_n\} In={y1,...,yn},定义统计量:
U Y = W X Y = # ( x i < y j , i ∈ I m , j ∈ I n ) U_Y=W_{XY}=\#(x_i \lt y_j,i \in I_m,j \in I_n) UY=WXY=#(xi<yj,i∈Im,j∈In)它表示所有的 X X X观测值和 Y Y Y观测值做比较之后, Y Y Y观测值大于 X X X观测值的个数。它是对 Y Y Y相对于 X X X的秩求和;
U X = W Y X = # ( y j < x i , i ∈ I m , j ∈ I n ) U_X=W_{YX}=\#(y_j \lt x_i,i \in I_m,j \in I_n) UX=WYX=#(yj<xi,i∈Im,j∈In)它表示所有的 X X X观测值和 Y Y Y观测值做比较之后, X X X观测值大于 Y Y Y观测值的个数。它是对 X X X相对于 Y Y Y的秩求和。
在零假设下, W X Y ( U Y ) W_{XY}(U_Y) WXY(UY)与 W Y X ( U X ) W_{YX}(U_X) WYX(UX)同分布。因为此时, X X X、 Y Y Y的样本观测值排序求秩,位置穿插比较均匀,秩和相近。称 W X Y ( U Y ) W_{XY}(U_Y) WXY(UY)或 W Y X ( U X ) W_{YX}(U_X) WYX(UX)为Mann-Whitney U统计量。显然, W X Y ( U Y ) W_{XY}(U_Y) WXY(UY)与 W Y X ( U X ) W_{YX}(U_X) WYX(UX)这两个统计量之间,是此消彼长的关系,且 U m a x = m n U_{max}=mn Umax=mn, U m i n = 0 U_{min}=0 Umin=0。当其中一个Mann-Whitney U统计量等于最大值 m n mn mn时,另一个Mann-Whitney U统计量必定等于最小值 0 0 0。
Mann-Whitney U统计量(公式法):根据定义,也可以用如下公式计算Mann-Whitney U统计量: U Y = W X Y = ∑ j = 1 n ( R j − j ) U_Y=W_{XY}=\sum_{j=1}^n(R_j-j) UY=WXY=j=1∑n(Rj−j)其中, j j j和 R j R_j Rj分别代表:将总体 Y Y Y的 n n n个数据从小到大排列求秩,相当于组内求秩, j j j即总体 Y Y Y各样本点的组内秩;再将总体 X X X的 m m m个样本和总体 Y Y Y的 n n n个样本混合,从小到大排列求秩,相当于组间求秩, R j R_j Rj即总体 Y Y Y的第 j j j个样本点在全体数据中的秩;
U X = W Y X = ∑ i = 1 m ( R i − i ) U_X=W_{YX}=\sum_{i=1}^m(R_i-i) UX=WYX=i=1∑m(Ri−i)其中, i i i和 R i R_i Ri分别代表:将总体 X X X的 m m m个数据从小到大排列求秩,相当于组内求秩, i i i即总体 X X X各样本点的组内秩;再将总体 X X X的 m m m个样本和总体 Y Y Y的 n n n个样本混合,从小到大排列求秩,相当于组间求秩, R i R_i Ri即总体 X X X的第 i i i个样本点在全体数据中的秩; -
统计量之间的转化:实际上,Wilcoxon秩和统计量与Mann-Whitney U统计量是等价的,因为二者之间可以相互转化:
U Y = W X Y = W Y − n ( n + 1 ) 2 U_Y=W_{XY}=W_Y-\frac{n(n+1)}{2} UY=WXY=WY−2n(n+1) U X = W Y X = W X − m ( m + 1 ) 2 U_X=W_{YX}=W_X-\frac{m(m+1)}{2} UX=WYX=WX−2m(m+1)
则 U Y + U X = W X Y + W Y X = ( m + n ) ( m + n + 1 ) 2 − [ n ( n + 1 ) 2 + m ( m + 1 ) 2 ] = m n U_Y+U_X=W_{XY}+W_{YX}=\frac{(m+n)(m+n+1)}{2}-[\frac{n(n+1)}{2}+\frac{m(m+1)}{2}]=mn UY+UX=WXY+WYX=2(m+n)(m+n+1)−[2n(n+1)+2m(m+1)]=mn -
为什么称为U统计量:以 W X Y ( U Y ) W_{XY}(U_Y) WXY(UY)为例,定义函数 ϕ ( x i , y j ) = { 1 , x i < y j 0 , x i ≥ y j \phi(x_i,y_j)=\left\{ \begin{aligned} 1,x_i<y_j \\ 0,x_i \ge y_j \\ \end{aligned} \right. ϕ(xi,yj)={1,xi<yj0,xi≥yj
则 U Y = W X Y = ∑ i = 1 m ∑ j = 1 n ϕ ( x i , y j ) U_Y=W_{XY}=\sum_{i=1}^m\sum_{j=1}^n\phi(x_i,y_j) UY=WXY=∑i=1m∑j=1nϕ(xi,yj)。将这 m n mn mn个 ϕ ( x i , y j ) \phi(x_i,y_j) ϕ(xi,yj)求平均,则有 U ( x 1 , . . . , x m ; y 1 , . . . , y n ) = U Y m n = W X Y m n = ∑ i = 1 m ∑ j = 1 n ϕ ( x i , y j ) m n U(x_1,...,x_m;y_1,...,y_n)=\frac{U_Y}{mn}=\frac{W_{XY}}{mn}=\frac{\sum_{i=1}^m\sum_{j=1}^n\phi(x_i,y_j)}{mn} U(x1,...,xm;y1,...,yn)=mnUY=mnWXY=mn∑i=1m∑j=1nϕ(xi,yj)
称 U ( x 1 , . . . , x m ; y 1 , . . . , y n ) U(x_1,...,x_m;y_1,...,y_n) U(x1,...,xm;y1,...,yn)为以 ϕ ( x i , y j ) \phi(x_i,y_j) ϕ(xi,yj)为核的两样本 x 1 , . . . , x m x_1,...,x_m x1,...,xm和 y 1 , . . . , y n y_1,...,y_n y1,...,yn的 U U U统计量。在 U U U的定义中,这些 ϕ ( x i , y j ) \phi(x_i,y_j) ϕ(xi,yj)在求平均时,它们有相等的权重,正是因为它们是均等(Uniform)的,所以把这种类型的统计量统称为 U U U统计量。
因此,U统计量的计算可以通过3种方法:【法1】直接用定义法手动数出
Y
Y
Y大于
X
X
X的个数、
X
X
X大于
Y
Y
Y的个数,分别得到
W
X
Y
(
U
Y
)
W_{XY}(U_Y)
WXY(UY)和
W
Y
X
(
U
X
)
W_{YX}(U_X)
WYX(UX);【法2】根据定义,用组间秩减去组内秩的公式;【法3】按照第1步计算Wilcoxon秩和统计量
W
X
W_X
WX和
W
Y
W_Y
WY,再按照第3步的关系计算
W
X
Y
(
U
Y
)
W_{XY}(U_Y)
WXY(UY)和
W
Y
X
(
U
X
)
W_{YX}(U_X)
WYX(UX)。
- 结合实例理解检验过程
回到最开始举的例子:对于真实样本健康(0)、得病(1)、健康(0)、健康(0)、得病(1),模型判断每个样本的得病概率是0.30,0.60,0.55,0.40,0.50,将两类样本分别按得病概率从小到大依次排序如下:
健
康
样
本
(
0
)
的
预
测
得
病
概
率
:
0.30
、
0.40
、
0.55
健康样本(0)的预测得病概率:0.30、0.40、0.55
健康样本(0)的预测得病概率:0.30、0.40、0.55
组
内
秩
:
1
,
2
,
3
组内秩:1,2,3
组内秩:1,2,3;
混
合
求
秩
(
组
间
秩
)
:
1
,
2
,
4
混合求秩(组间秩):1,2,4
混合求秩(组间秩):1,2,4
得
病
样
本
(
1
)
的
预
测
得
病
概
率
:
0.50
、
0.60
得病样本(1)的预测得病概率:0.50、0.60
得病样本(1)的预测得病概率:0.50、0.60
组
内
秩
1
,
2
组内秩1,2
组内秩1,2;
混
合
求
秩
(
组
间
秩
)
:
3
,
5
混合求秩(组间秩):3,5
混合求秩(组间秩):3,5
-
Wilcoxon秩和统计量:将所有样本概率混合求秩,分别得到健康样本的秩和 W 0 = 1 + 2 + 4 = 7 W_0=1+2+4=7 W0=1+2+4=7,得病样本的秩和 W 1 = 3 + 5 = 8 W_1=3+5=8 W1=3+5=8。且 n 0 = 3 n_0=3 n0=3, n 1 = 2 n_1=2 n1=2,则 W 0 + W 1 = ( n 0 + n 1 ) ( n 0 + n 1 + 1 ) 2 = 15 W_0+W_1=\frac{(n_0+n_1)(n_0+n_1+1)}{2}=15 W0+W1=2(n0+n1)(n0+n1+1)=15。 -
Mann-Whitney U统计量(定义法):在这个例子中,判别二分类模型的优劣时,由于模型输出的是得病概率,我们希望模型对得病样本的预测值应尽量高,而健康样本的预测值应尽量低,最好能够使得病样本的最小预测值仍高于健康样本的最高预测值。因此要考察的统计量应该是 W 01 ( U 1 ) W_{01}(U_1) W01(U1):即给定任意一个得病样本的预测概率,考察它大于健康样本的预测概率的个数。对于得病概率 0.50 0.50 0.50,它大于 0.30 0.30 0.30、 0.40 0.40 0.40;对于得病概率 0.60 0.60 0.60,它大于 0.30 0.30 0.30、 0.40 0.40 0.40和 0.55 0.55 0.55;故 W 01 ( U 1 ) = 2 + 3 = 5 W_{01}(U_1)=2+3=5 W01(U1)=2+3=5。这里顺便计算 W 10 ( U 0 ) = 1 W_{10}(U_0)=1 W10(U0)=1。
Mann-Whitney U统计量(公式法): W 01 ( U 1 ) = ( 3 − 1 ) + ( 5 − 2 ) = 5 W_{01}(U_1)=(3-1)+(5-2)=5 W01(U1)=(3−1)+(5−2)=5 W 10 ( U 0 ) = ( 1 − 1 ) + ( 2 − 2 ) + ( 4 − 3 ) = 1 W_{10}(U_0)=(1-1)+(2-2)+(4-3)=1 W10(U0)=(1−1)+(2−2)+(4−3)=1对这个公式直观理解是:用组间秩减去组内秩,得到一组样本点大于另一组样本点的总个数。 -
统计量之间的转化: W 01 ( U 1 ) = W 1 − n 1 ( n 1 + 1 ) 2 = 8 − 3 = 5 W_{01}(U_1)=W_1-\frac{n_1(n_1+1)}{2}=8-3=5 W01(U1)=W1−2n1(n1+1)=8−3=5,结果同第2步。顺便计算 W 10 ( U 0 ) = W 0 − n 0 ( n 0 + 1 ) 2 = 7 − 6 = 1 W_{10}(U_0)=W_0-\frac{n_0(n_0+1)}{2}=7-6=1 W10(U0)=W0−2n0(n0+1)=7−6=1。则 U 0 + U 1 = W 10 + W 01 = n 0 n 1 = 6 U_0+U_1=W_{10}+W_{01}=n_0n_1=6 U0+U1=W10+W01=n0n1=6。
至此,结合上述例子,可以用Mann-Whitney U统计量很好地解释AUC值的含义,由于:
A
U
C
=
U
1
n
1
n
0
AUC = \frac{U_1}{n_1n_0}
AUC=n1n0U1其中,统计量
U
1
U_1
U1代表:模型预测得病样本的得病概率大于健康样本的得病概率的个数,即
c
o
u
n
t
(
P
实
际
得
病
>
P
实
际
健
康
)
count(P_{实际得病}>P_{实际健康})
count(P实际得病>P实际健康),是正向指标;统计量
U
0
U_0
U0代表:模型预测健康样本的得病概率大于得病样本的得病概率的个数,即
c
o
u
n
t
(
P
实
际
健
康
>
P
实
际
得
病
)
count(P_{实际健康}>P_{实际得病})
count(P实际健康>P实际得病),是负向指标;且统计量
U
1
U_1
U1和
U
0
U_0
U0之和是两组样本的总配对数量
n
1
n
0
n_1n_0
n1n0。模型性能越好,统计量
U
1
U_1
U1的值越大,其在
n
1
n
0
n_1n_0
n1n0之中所占的比重就越大,因此,AUC值可以理解为:
A
U
C
=
U
1
U
1
+
U
0
=
c
o
u
n
t
(
P
实
际
得
病
>
P
实
际
健
康
)
c
o
u
n
t
(
P
实
际
得
病
>
P
实
际
健
康
)
+
c
o
u
n
t
(
P
实
际
健
康
>
P
实
际
得
病
)
AUC=\frac{U_1}{U_1+U_0}=\frac{count(P_{实际得病}>P_{实际健康})}{count(P_{实际得病}>P_{实际健康})+count(P_{实际健康}>P_{实际得病})}
AUC=U1+U0U1=count(P实际得病>P实际健康)+count(P实际健康>P实际得病)count(P实际得病>P实际健康)即:
A
U
C
=
P
(
P
实
际
得
病
>
P
实
际
健
康
)
AUC=P(P_{实际得病}>P_{实际健康})
AUC=P(P实际得病>P实际健康)或者更通俗一点地理解:模型将1样本预测为1的概率为
P
1
P_1
P1,将0样本预测为1的概率为
P
0
P_0
P0,则
P
1
>
P
0
P_1>P_0
P1>P0的概率即为AUC,它反应了分类器对样本的排序能力。用R语言实现Mann-Whitney U检验:
> health <- c(0.30, 0.40, 0.55 )
> illness <- c(0.50, 0.60)
> wilcox.test(illness, health, alternative = 'greater')
Wilcoxon rank sum test
data: illness and health
W = 5, p-value = 0.2
alternative hypothesis: true location shift is greater than 0
参考资料:
第一型及第二型错误
维基百科:ROC曲线
ROC和AUC介绍以及如何计算AUC
关于AUC,你应该知道的和可能不知道的
Wikipedia:False positives and false negatives
Type I error & Type II error 与 false positives & false negatives
ROC曲线的进一步学习(关于那条对角线)
分类模型的性能评估——以 SAS Logistic 回归为例 (2): ROC 和 AUC
Wikipedia:Sign test
Wikipedia:Wilcoxon signed-rank test
符号检验和Wilcoxon符号秩检验
Wikipedia:Mann–Whitney U test
ROC分析当中的AUC和Mann-Whitney U statistic的关系
《非参数统计》王星/褚挺进
百度文库:Mann-Whitney U 统计量检验法
The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve (1982)
Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation (2002)
Latex数学公式
浅谈ROC曲线







 本文深入探讨了ROC曲线的概念及其在模型评估中的应用,详细解释了第一类和第二类错误,介绍了ROC曲线的起源和发展历程。同时,文章还解析了AUC值的计算方法及其与Mann-Whitney U检验的关系。
本文深入探讨了ROC曲线的概念及其在模型评估中的应用,详细解释了第一类和第二类错误,介绍了ROC曲线的起源和发展历程。同时,文章还解析了AUC值的计算方法及其与Mann-Whitney U检验的关系。
















 1343
1343

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








