特征选择:子集搜索与评价
属性:特征
- 相关特征:对当前学习任务有用的特征;
- 无关特征:对当前学习任务无用的特征;
特征选择(数据预处理的一种):从给定的特征集合中选出相关特征子集的过程;
特征选择的原因:
- 减轻由于属性过多造成的维数灾难;
- 去除不相关特征降低学习任务的难度;
冗余特征:Eg:知道立方体的长、宽,立方体的底面积就是冗余特征;有时候会增加学习任务难度,但冗余特征作为“中间概念”的时候方便计算,比如,计算立方体的体积,立方体的底面积会加快速度;
面临两个问题:
- 1、如何根据评价结果获取下一个候选特征子集?
- 2、如何评价候选自己的好坏?
环节一:子集搜索
- 前向搜索:先确定一个子集,依次增加特征,构成候选子集,选出最优,继续指导最优的特征子集步入上一个子集,将其作为特征选择的结果。
- 后向搜索:先将整个特征集合作为候选子集,依次去除不相关特征;
- 双向搜索:前向和后向结合;
环节二:子集评价
评价准则:属性子集的信息增益:
信息增益Gain(A)越大,特征子集A包含的有助于分类的信息越多。
特征选择方法:过滤式、包裹式、嵌入式
过滤式选择
过滤式方法是一种将特征选择与学习器训练相分离的特征选择技术。
1、先将相关特征挑选出来;
2、再使用选择出的数据子集来训练学习器。
Relief算法:二分类问题
思想:使用一个“相关统计量”来度量特征的重要性,该统计量是一个向量,其中每个分量代表着相应特征的重要性,因此我们最终可以根据这个统计量各个分量的大小来选择出合适的特征子集。
对于数据集中的每个样例xi,首先找出与xi同类别的最近邻与不同类别的最近邻,分别称为猜中近邻(near-hit)与猜错近邻(near-miss),接着便可以分别计算出相关统计量中的每个分量。对于j分量:
直观上理解:对于猜中近邻,两者j属性的距离越小越好,对于猜错近邻,j属性距离越大越好。更一般地,若xi为离散属性,diff取海明距离,即相同取0,不同取1;若xi为连续属性,则diff为曼哈顿距离,即取差的绝对值,Xa在属性j三的取值均规范化到[0,1],分别计算每个分量,最终取平均便得到了整个相关统计量。
Relief-F:多分类问题
对于j分量,新的计算公式如下:
其中pl表示第l类样本在数据集中所占的比例,易知两者的不同之处在于:标准Relief 只有一个猜错近邻,而Relief-F有多个猜错近邻。
注:Relief只需在数据记得采样上而不是这个数据集上估计相关统计量,且属于高效的过滤式特征选择算法。
包裹式选择
包裹方法是一种为给定学习器选择最有利于其性能的特征子集(量身定做)。
LVW包裹式算法:拉斯维加斯框架下采用随机策略进行子集搜索,以最终很累起的误差为特征自己的评价准则;
拉斯维加斯和蒙特卡罗方法均是以赌城名的方法: 有时间限制:拉斯维加斯可能给出也可能不给出解;蒙特卡罗一定给出解,虽然不一定是对的; 无时间限制:均可以给出解; 蒙特卡罗算法:采样越多,越近似最优解,一定会给出解,但给出的解不一定是正确解; |
注:包裹式比过滤式特征选择更好;但是计算开销更大;
嵌入式与L1正则化
过滤式中特征选择与后续学习器完全分离;包裹式则是使用学习器作为特征选择的评价准则;
嵌入式选择:一种将特征选择与学习器训练完全融合的特征选择方法,即将特征选择融入学习器的优化过程中。
机器学习的核心任务就是:在模型简单的基础上保证模型的契合度(经验风险指的是模型与训练数据的契合度,结构风险则是模型的复杂程度)。
例如:
岭回归ridge regression:
加上了L2范数的最小二乘法,有效地解决了奇异矩阵、过拟合等诸多问题,下面的嵌入式特征选择则是在损失函数后加上了L1范数。
最小绝对收缩选择算子LASSO:
加上了L1范数。
L1范数会趋向产生少量的特征(稀疏解),其求得的w会有更少的非零分量;
L2会选择更多的特征,这些特征的权值都会接近于0;
这样L1范数在特征选择上就十分有用,而L2范数则具备较强的控制过拟合能力。可以从下面两个方面来理解:
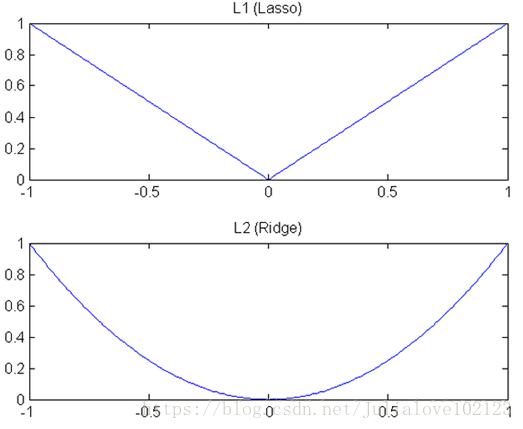
(1)下降速度:L1范数按照绝对值函数来下降,L2范数按照二次函数来下降。因此在0附近,L1范数的下降速度大于L2范数,故L1范数能很快地下降到0,而L2范数在0附近的下降速度非常慢,因此较大可能收敛在0的附近。
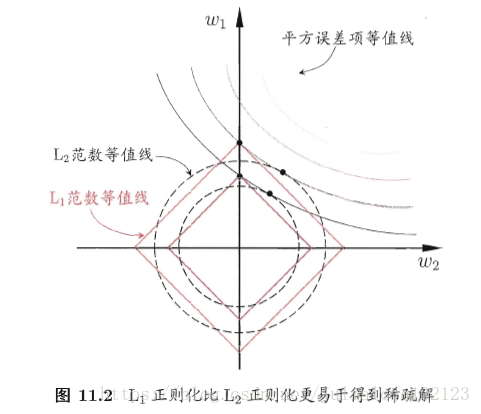
(2)空间限制:L1范数与L2范数都试图在最小化损失函数的同时,让权值W也尽可能地小。我们可以将原优化问题看做为下面的问题,即让后面的规则则都小于某个阈值。这样从图中可以看出:L1范数相比L2范数更容易得到稀疏解。
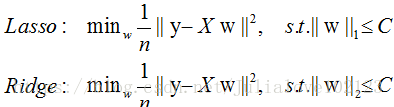
稀疏表示与字典学习
稀疏性表现1:数据集D矩阵中,去除很多表示特征的列;
稀疏性表现2:数据集D矩阵中存在很多0元素,且没有出现在同一列中;
当样本数据是一个稀疏矩阵时,对学习任务来说会有不少的好处,例如很多问题变得线性可分,储存更为高效等。这便是稀疏表示与字典学习的基本出发点。
稀疏编码(sparse coding)/字典学习(dictionary learning)/码书(codebook)学习:对于一个给定的稠密矩阵,若能通过某种方法找到其合适的稀疏(恰当稀疏)表示,则可以使得学习任务更加简单高效.
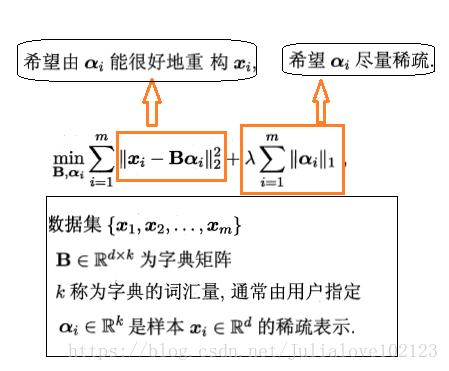
给定一个数据集,字典学习/稀疏编码指的便是通过一个字典将原数据转化为稀疏表示,因此最终的目标就是求得字典矩阵B及稀疏表示α,书中受LASSO的启发,使用变量交替优化的策略能较好地求解。
字典学习:
求解略。
注:
- 稀疏学习侧重于对样本进行稀疏性表达的过程;
- 字典学习侧重于学得字典的过程;
压缩感知
通过欠采样信息来恢复全部信息。在实际问题中,为了方便传输和存储,我们一般将数字信息进行压缩,这样就有可能损失部分信息,如何根据已有的信息来重构出全部信号,这便是压缩感知的来历,压缩感知的前提是已知的信息具有稀疏表示。
压缩感知:
- 感知测量:对原始信号进行处理以获得稀疏表示;Eg:傅里叶变换、小波变换、字典学习、稀疏编码等;
- 重构恢复:基于稀疏性从少年的观测中恢复原信号(压缩感知的精髓);
基本知识补充:
奈奎斯特采样定理 :
如果对某一时间连续信号(模拟信号)进行采样,当采样速率达到被测信号最大频率的两倍时,那么,根据这些采样值就能准确地确定原信号
限定等距性RIP(Restricted Isometry Property):
对大小为n * m的矩阵A,若存在常数δk∈(0,1)使得任意向量s和A的所有子矩阵Ak∈Rn*k有
![]()
则称A满足k限定等距性。通过下面优化近乎完美的从y中恢复出稀疏信号s,进而恢复x:
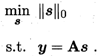
L0范数的最小化是一个NP难题,L1范数最小化在一定条件下与L0最小化共解,则:
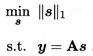
该式可以转化为LASSO的等价形式通过近端梯度下降求解,即“基寻踪去噪”
基寻踪去噪Basis Pursuit De-Noising:
http://www.elecfans.com/video/yinpinjishu/20171201590829_a.html
https://blog.csdn.net/jbb0523/article/details/52013669
矩阵补全技术:
https://www.zhihu.com/question/47716840
半正定规划SDP(Semi-Definite Programming):
https://blog.csdn.net/sunmenggmail/article/details/13998255
------*-*---------------------------------------------------------------------------------------------------------*-*----
更多详细内容请关注公众号:目标检测和深度学习
-------…^-^……----------------------------------------------------------------------------------------------------------…^-^……--








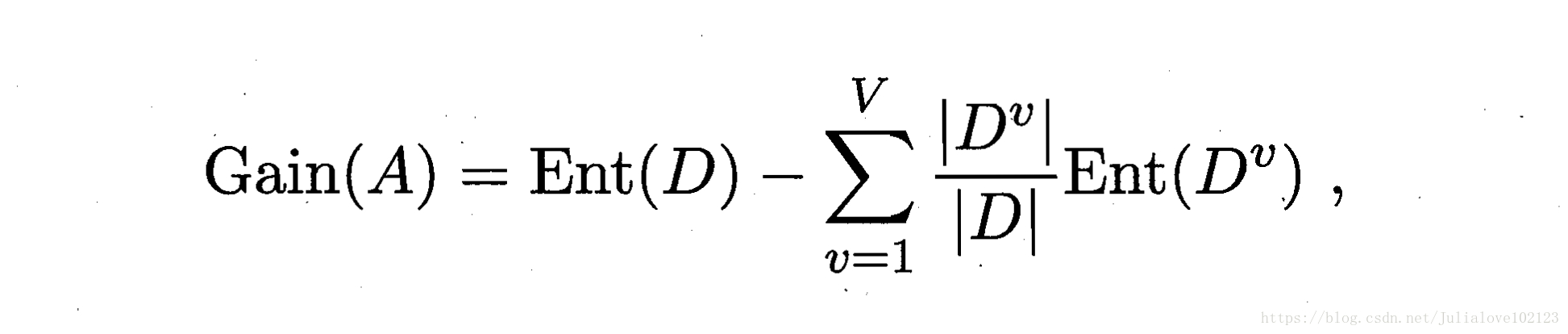
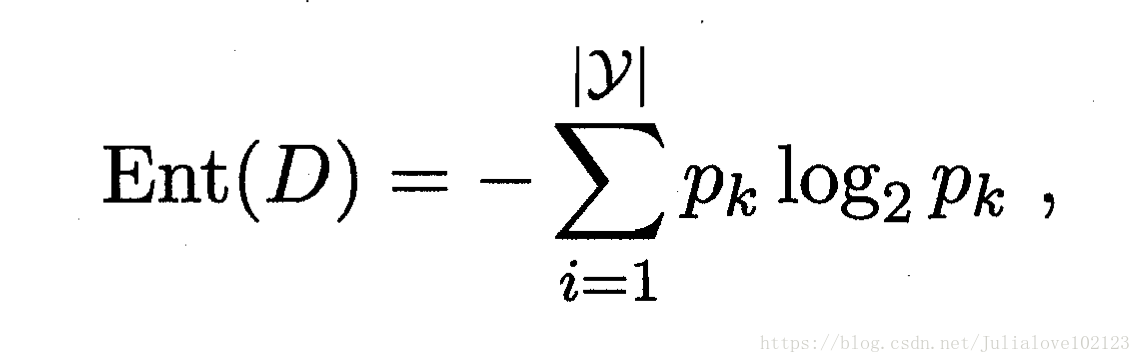
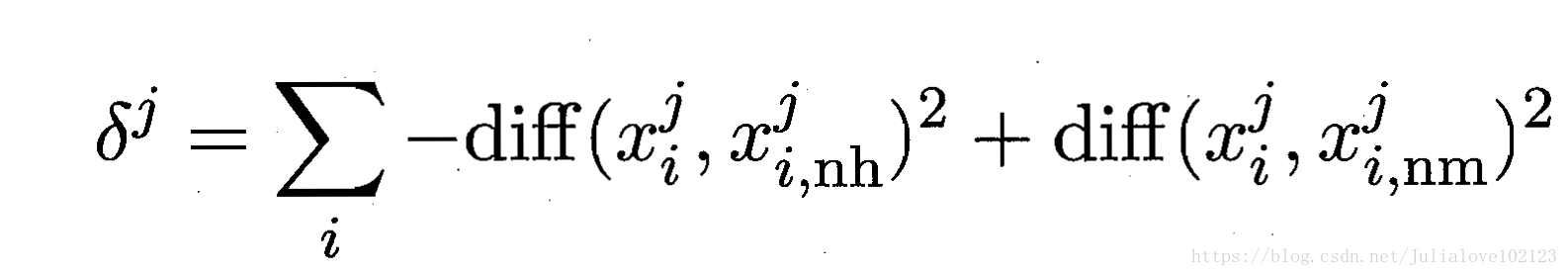
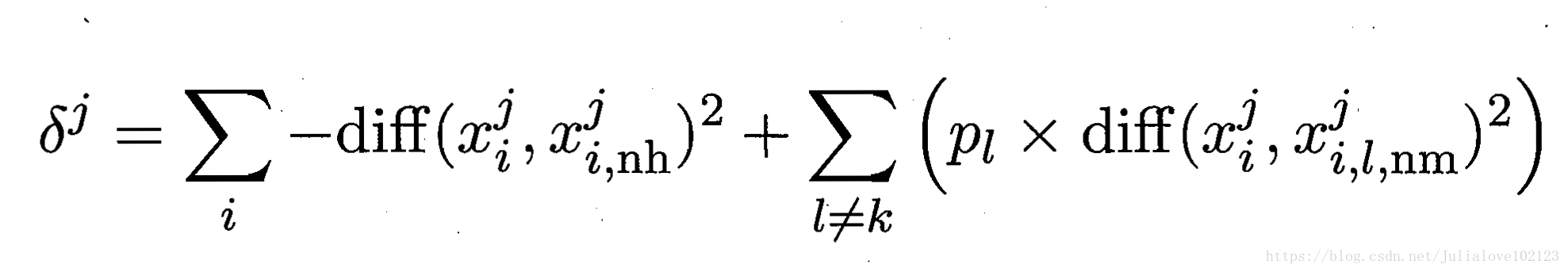

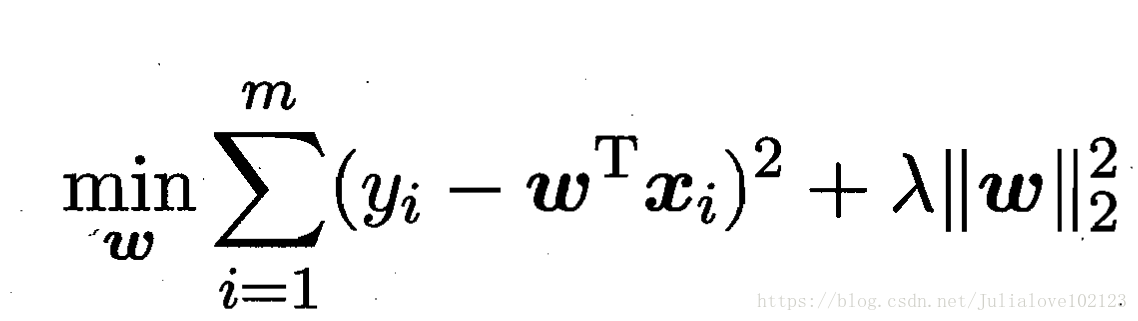
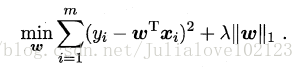















 1068
1068











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










