Sicily 1527. Tiling a Grid With Dominoes

1527. Tiling a Grid With Dominoes
Description
We wish to tile a grid 4 units high and N units long with rectangles (dominoes) 2 units by one unit (in either orientation). For example, the figure shows the five different ways that a grid 4 units high and 2 units wide may be tiled.

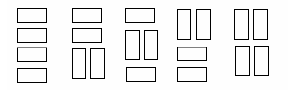
Write a program that takes as input the width, W , of the grid and outputs the number of different ways to tile a 4-by-W grid.

Input
The first line of input contains a single integer N , (1<=N<=1000) which is the number of datasets that follow.

Each dataset contains a single decimal integer, the width, W , of the grid for this problem instance.

Output
For each problem instance, there is one line of output: The problem instance number as a decimal integer (start counting at one), a single space and the number of tilings of a 4-by-W grid. The values of W will be chosen so the count will fit in a 32-bit integer.
Sample Input
3
2
3
7
Sample Output
1 5
2 11
3 781

一. 题意理解
现有长为 2，宽为 1 的多米诺骨牌，给定一个长为 n，宽为 4 的矩形区域，要求使用多米诺骨牌完美覆盖这个区域，并且算出覆盖的方法数。

二. 解题思路
对于这种完美覆盖问题，有一种比较通用的方法：列出所有的基本状态，再考虑状态之间的转换关系。在列举的时候，我们的思考要有方向性，要有一个特定的规则。如若我们想到什么列什么，很容易漏掉一些情况。我们不妨用如下的规则列举：用二维数组 f[i][j]表示前 i 列已经完美覆盖，第 i+1列的状态为 j，j一共有如下5中情况：


解释：我们用4位数表示每个状态，第一行有突出，则为1；没有突出，则为0。比如，j=4的情况，第一、第四行没有突出，二、三行有突出，它的状态就是0110。至于j等于几对应什么状态则无所谓。接下来我们来找状态转移方程。
以 f[i][0]为例。它的前 i 列铺满了，第 j+1 列没有突出。它可以由 f[i-1][0]得出(补上两块构成的 4×1 区域)；可以由 f[i-1][1]得出(右下角补上一块） ；可以由 f[i-1][2]得出(右上角补上一块)；可以由 f[i-1][3]
得出（中间补上一块） ；无法由 f[i-1][4]得出。注意特殊情况：可以直接由 f[n-2]得出（补上 4 块构成的 4×4 区域）。其他状态也是如此递推。注意f[0][0]为1！状态转移方程如下：
• f[i][0] = f[i-1][0] + f[i-1][1] + f[i-1][2] + f[i-1][3] + f[i-2][0]
• f[i][1] = f[i-1][0] + f[i-1][2]
• f[i][2] = f[i-1][0] + f[i-1][1]
• f[i][3] = f[i-1][0] + f[i-1][4]
• f[i][4] = f[i-1][3]

三. 代码实现

#include<iostream>
#include<string.h>
using namespace std;
int f[1005][5];

int Domi(int n) {
	f[0][0] = 1;
	for (int i = 1; i <= n; ++i) {
		f[i][0] = f[i - 1][0] + f[i - 1][1] + f[i - 1][2] + f[i - 1][3];
		if (i > 1) f[i][0] += f[i - 2][0];
		f[i][1] = f[i - 1][0] + f[i - 1][2];
		f[i][2] = f[i - 1][0] + f[i - 1][1];
		f[i][3] = f[i - 1][0] + f[i - 1][4];
		f[i][4] = f[i - 1][3];
	}
	return f[n][0];
}

int main() {
	int n;
	cin >> n;
	int counter = 1;
	for (int i = 0; i < n; ++i) {
		int num;
		cin >> num;
		memset(f, 0, sizeof(f));
		cout << counter << " " << Domi(num) << endl;
		counter++;
	}
	return 0;
}

四. 时间复杂度分析：算法的时间复杂度为O(n)。