汉诺塔问题，汉诺塔问题变形，归纳法，取模（加减乘除取模，大数取模问题，阶乘取模且模小的情况的技巧，快速幂输出最后三位数的问题）

目录

汉诺塔问题

递归 解题思路：

汉诺塔问题变形

归纳法

取模

加法取模

减法取模

乘法取模

除法取模

大数取模问题

字符串按位相加进位模拟 解题思路：

阶乘取模且模小的情况的技巧

快速幂输出最后三位数的问题

快速幂 解题思路：

---

汉诺塔问题

输入一个n，代表A柱上有n个盘子，每次只能移动一个，且小盘子必须在大盘子的上边，求输出A柱所有盘子移动到B柱的操作

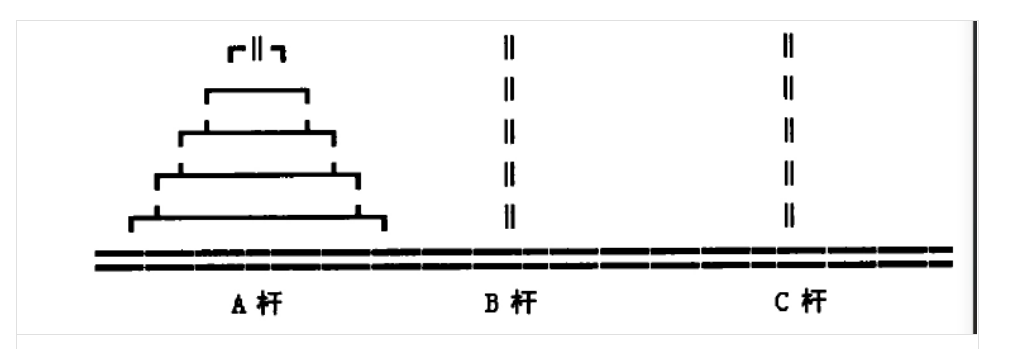
递归 解题思路：

首先思考递归出口，n==1的情况下，我们只需要输出A-->B即可，然后对于这个问题，如果能够实现n-1个盘子被人移动到了C柱上，我们只需要将第n个盘子移动到B柱上，然后再让n-1个盘子移回到B柱上即可

#include <iostream>

using namespace std;

void hnt(int n, char A, char B, char C)
{
    //n==1时，只要输出一个A-->B即可
    if(n == 1)
    {
        cout << "第1个盘子:" << A << "--》" << B << endl;
        return;
    }
    //假设有人可以帮我实现n-1的盘子都移动到C
    hnt(n-1, A, C, B);
    //那么我只要输出第n个盘子从A-->B
    cout << "第" << n << "个盘子:" << A << "--》" << B << endl;
    //再假设有人可以帮我实现n-1的盘子都从C都移动到B，任务就完成了
    hnt(n-1, C, B, A);
}

int main()
{
    int n;
    cin >> n;
    hnt(n, 'A', 'B', 'C');
    return 0;
}

汉诺塔问题变形

把有 n 个圆盘的塔从左边的桩柱A移动到右边的桩柱B，不允许在A和B之间直接移动，求最短的移动序列．（每一次移动都必须是移动到中间的桩柱或者从中间的桩柱移出．像通常一样，较大的圆盘永远不能放在较小圆盘的上面．）

这个题我也不会

归纳法

假如有一个公式 ，已知f(1)为1，要求证这个公式是否成立，我们只需计算出是否成立，如果成立则代表成立

取模

加法取模

对于a + b的取模，可以提前对a和b进行取模再相加再取模是没有影响的

(a + b) % n == (a % n + b % n) % n

减法取模

对于a - b的取模，因为要考虑到a - b为负数的情况，所以我们要将取模后的值围绕成一个环形（假如取模5，那么在0、1、2、3、4上对应的是一个序列，类似于约瑟夫环问题），所以在对a%n，b %n相减后，加上一个n，确保变成了正数，最后又要%n，为了防止原先的数字加上n后变成了5

(a - b) % n == ((a % n - b % n) + n) % n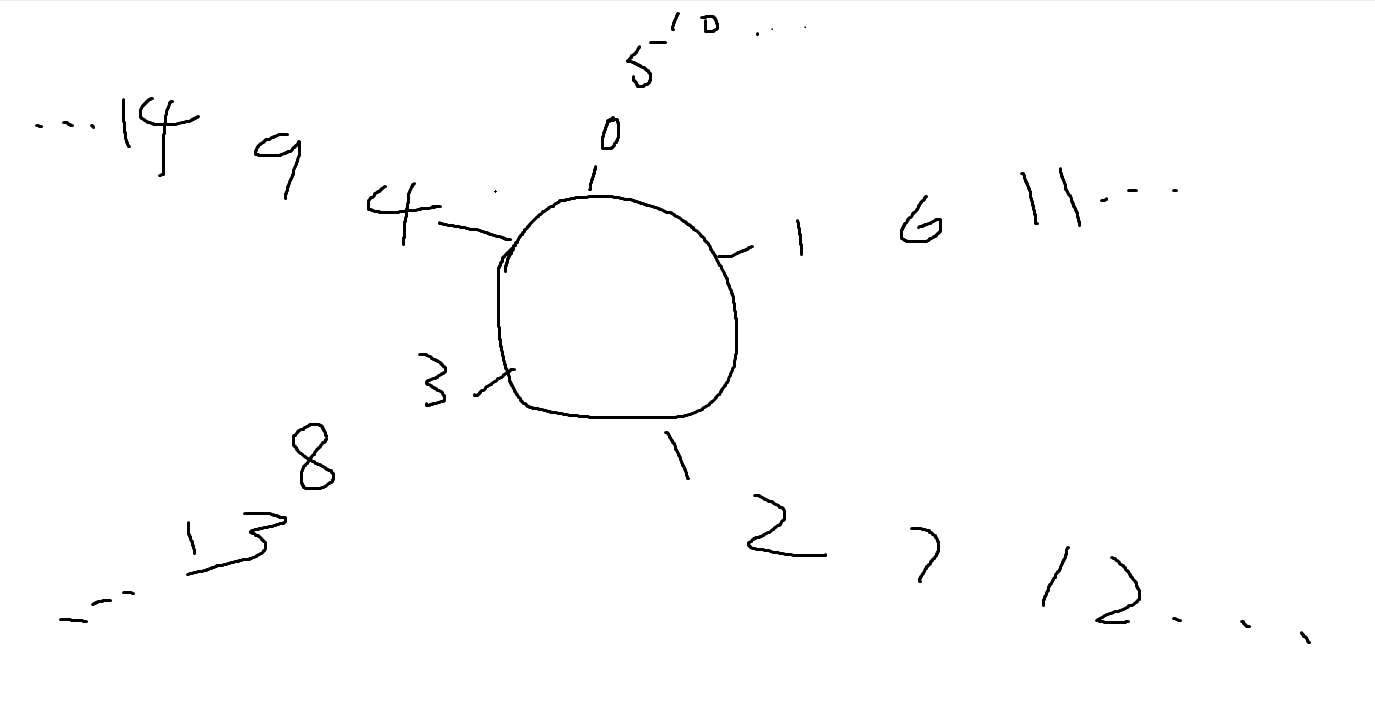

乘法取模

乘法取模和加法同理

(a * b) % n == ((a % n) * (b % n) + n) % n

除法取模

------------待补充

(a / b) % n == 

大数取模问题

给定一个mod = 1e9 +7，输入一个很大很大的数字，要求输出对mod取模后的结果

字符串按位相加进位模拟 解题思路：

首先这个数字很大，long long存不下，所以用string，然后根据加法取模的性质，进行每次拿一位出来再乘十，然后就取模一次，保证他不会爆掉（关于答案是否正确，直接记住概念是正确的就行吗，举个例子，当一个数字进行模拟，然后3000 % 3000 和300000 % 3000的答案是一样的）

#include <iostream>
using namespace std;
const int mod = 1e9 + 7;

int main()
{
    //保证存下比long long还大的数
    string a;
    cin >> a;
    int ans = 0;
    for(auto i: a)
    {
        //一位一位的取出然后乘十（之所以这样写是因为，第一次要先乘再加，不然到最后就多乘了一个10）
        ans = (ans * 10 + (i - '0')) % mod;
    }
    cout << ans;
    return 0;
}

阶乘取模且模小的情况的技巧

我们对一个阶乘进行取模操作，且模小的情况，如果阶乘数字>=模，则取模为0（不一定要判断到>=，因为前面所判断到的数字，可能相乘起来已经包括了 模 这个因子）

#include <bits/stdc++.h>
using namespace std;

int main()
{
    string a;
    cin >> a;
    int mod = 666;
    if (a.size() > 3) {
        cout << 0 << endl;
        return 0;
    }
    return 0;
}

快速幂输出最后三位数的问题

给定一个A，B，求A的B次方的值的最后三位

快速幂 解题思路：

单纯的靠暴力去循环，复杂度是O(B)，如果B=100000000，那么就要算很久，现在来假设3^10

3^10=3*3*3*3*3*3*3*3*3*3

//尽量想办法把指数变小来，这里的指数为10

3^10=(3*3)*(3*3)*(3*3)*(3*3)*(3*3)

3^10=(3*3)^5

3^10=9^5

//此时指数由10缩减一半变成了5，而底数变成了原来的平方，求3^10原本需要执行10次循环操作，求9^5却只需要执行5次循环操作，但是3^10却等于9^5,我们用一次（底数做平方操作）的操作减少了原本一半的循环量，特别是在幂特别大的时候效果非常好

//现在我们的问题是如何把指数5变成原来的一半，5是一个奇数，5的一半是2.5，但是我们知道，指数不能为小数，因此我们不能这么简单粗暴的直接执行5/2，然而，这里还有另一种方法能表示9^5

9^5=（9^4）*（9^1）

//此时我们抽出了一个底数的一次方，这里即为9^1，这个9^1我们先单独移出来,剩下的9^4又能够在执行“缩指数”操作了，把指数缩小一半，底数执行平方操作

9^5=（81^2）*(9^1)

//把指数缩小一半，底数执行平方操作

9^5=（6561^1）*(9^1)

//此时，我们发现指数又变成了一个奇数1，按照上面对指数为奇数的操作方法，应该抽出了一个底数的一次方，这里即为6561^1，这个6561^1我们先单独移出来，但是此时指数却变成了0，也就意味着我们无法再进行“缩指数”操作了。

9^5=（6561^0）*(9^1)*(6561^1)=1*(9^1)*(6561^1)=(9^1)*(6561^1)=9*6561=59049

我们能够发现，最后的结果是9*6561，而9是怎么产生的？是不是当指数为奇数5时，此时底数为9。那6561又是怎么产生的呢？是不是当指数为奇数1时，此时的底数为6561。所以我们能发现一个规律：最后求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积

#include <iostream>

using namespace std;

int ksm(long long a, long long b)
{
    long long m = 1;
    while(b > 0)
    {
        /*if(b & 1)//if(b % 2 ==0)
        {
            //这里是记录对底数进行平方的操作，然后可以将指数除以二
            m = m * a % 1000;
            b /= 2;
        }
        else
        {
            b -= 1;
            b /= 2;
            a = a * a % 1000;
        }

    }*/
        if(b & 1)//if(b % 2 ==0)
        {
            //这里是记录对底数进行平方的操作，然后可以将指数除以二
            m = m * a % 1000;
        }
            //这里的优化是因为 b-1 后 b/2 等于 b/2
            //b /= 2;
            //这里的优化是因为b往后移动一位就是除以2
            b >>= 1;
            a = a * a % 1000;
    }
    //m是指数为奇数的情况下，所有底的乘积，且每次相乘都取模1000保留后三位
    return m;
}

int main()
{
    int a, b;
    cin >> a >> b;
    cout << ksm(a, b);
    return 0;
}