前言
请跟着上一讲http://blog.csdn.net/jurbo/article/details/52586981继续学习
2.1 线性表及其实现
2.1.1 引子:多项式表示
【例】:一元多项式及其运算
一元多项式: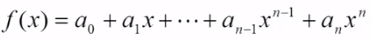
主要运算:多项式相加、相减、相乘等
【分析】如何表示多项式?
多项式的关键数据:
- 多项式项数n
- 各项系数及指数
方法1:顺序存储结构直接表示
方法2:顺序存储结构表示非零项
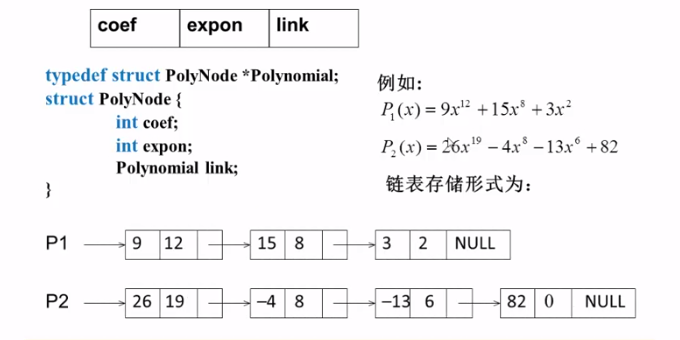
方法3:链表结构存储非零项
链表中每个结点存储多项式中的一个非零项,包括系数和指数两个数据域以及一个指针域。
2.1.2 线性表及顺序存储
多项式表示问题的启示
- 同一个问题可以有不同的表示(存储)方法
- 有一类共性问题:有序线性序列的组织和管理
线性表的定义
线性表由同类型数据元素构成有序序列的线性结构
- 表中元素个数称为线性表的长度
- 线性表没有元素时,称为空表
- 表起始位置称表头,表结束位置称表尾
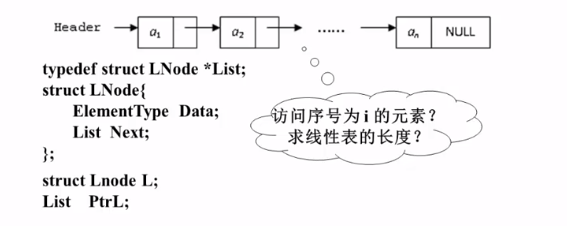
线性表的抽象数据类型描述
线性表的顺序存储实现
利用数组的连续存储空间顺序存放线性表的各元素
长度:因为数组是从0开始的,所以是last+1
顺序表主要操作的实现(初始化和查找)
初始化(建立空的顺序表)
List MakeEmpty()
{
List PtrL;
PtrL=(list)malloc(sizeof(struct LNode));
PtrL->Last=-1;
return PtrL;
}查找
int Find(ElementType X,List PtrL)
{
int i=0;
while(i<=PtrL->Last&&PtrL->Data[i]!=X)
i++;
if(i>PtrL->Last)
return -1;
else
return i;
}2.1.3 顺序存储的插入和删除
插入(第i个位置插入一个值为X的新元素)
void Insert(ElementType X,int i,List PtrL)
{
int j;
if(PtrL->Last==MAXSIZE-1) //表空间已满,不能插入
{
printf("表满");
return;
}
if(i<1||i>PtrL->Last+2)
{
printf("位置不合法");
return;
}
for(j=PtrL->Last;j>=i-1;j--)
PtrL->Data[j+1]=PtrL->Data[j]; //将a[i]-a[n]倒序向后移动
PtrL->Data[i-1]=X; //新元素插入
PtrL->Last++; //Last仍指向最后元素
return;
}删除(删除第i个元素)
void Delete(int i,List PtrL)
{
int j;
if(i<1||i>PtrL->Last+1)
{
printf("不存在第%d个元素",i);
return;
}
for(j=i;j<=PtrL->Last;j++)
PtrL->Data[j-1]=PtrL->Data[j];//将a[i+1]-a[n]向前移动
PtrL->Last--; //Last仍指向最后元素
return;
}2.1.4 线性表的链式存储实现
不要求逻辑上相邻的两个元素物理上也相邻;通过“链”建立起数据元素之间的逻辑关系。
插入、删除不需要移动数据元素,只需要修改“链”
求表长
int Length(List PtrL)
{
List p=PtrL;
int j=0;
while(p)
{
p=p->next;
j++;
}
return j;查找
(1)按序号查找
List FindKth(int K,List PtrL)
{
List p=PtrL;
int i=1;
while(p!=NULL&&i<K)
{
p=p->Next;
i++;
}
if(i==K)
return p;
else
return NULL;
}(2)按值查找
List Find(ElementType X,List PtrL)
{
List p=PtrL;
while(p!=NULL**p->Data!=X)
p=p->Next;
return p;
}2.1.5 链式存储的插入和删除
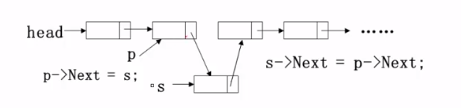
插入(在第i-1个节点后插入一个值为X的新结点)
(1)先构造一个新结点,用s指向
(2)再找到链表的第i-1个结点,用p指向
(3)然后修改指针,插入结点(p之后插入新结点是s)
List Insert(ElementType X,int i,List PtrL)
{
List p,s;
if(i==1) //新结点插入在表头
{
s=(List)malloc(sizeof(struct LNode)); //申请填充结点
s->Data=X;
s->Next=PtrL;
return s; //返回新表头指针
}
p=FindKth(i-1,PtrL); //查找第i-1个结点
if(p==NULL)
{
printf("参数i错");
return NULL;
}
else
{
s=(List)malloc(sizeof(struct LNode));
s->Data=X;
s->Next=p->Next;
p->Next=s;
return PtrL
}
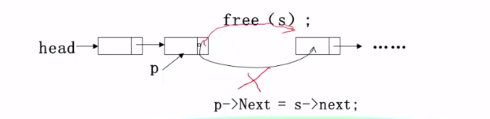
}删除(删除链表的第i个结点)
(1)先找到链表的第i-1个结点,用p指向
(2)再用指针s指向要被删除的结点(p的下一个结点)
(3)然后修改指针,删除s所指结点
(4)最后释放s所指结点的空间
List Delete(int i,List PtrL)
{
List p,s;
if(i==1) //若要删除的是表的第一结点
{
s=PtrL; //s指向第1个结点
if(PtrL!=NULL)
PtrL=PtrL->Next;
else
return NULL;
free(s);
return PtrL;
}
p=FindKth(i-1,PtrL); //查找第i-1个结点
if(p==NULL)
printf("第%d个结点不存在",i-1);
return NULL;
else if(p->Next==NULL)
{
printf("第%d个结点不存在",i);
return NULL;
}
else
{
s=p->Next; //s指向第i个结点
p->Next=s->Next; //从链表中删除
free(s);
return PtrL;
}
}2.1.6 广义表与多重链表
广义表
【例】:我们知道了一元多项式的表示,那么二元多项式又该如何表示?
比如:给定二元多项式:
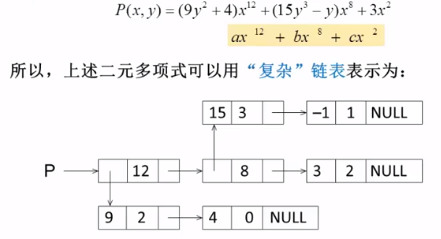
【分析】可以将上述二元多项式看成关于x的一元多项式
广义表
- 广义表是线性表的推广
- 对于线性表而言,n个元素都是基本的单元素
广义表中,这些元素不仅可以是单元素也可以是另一个广义表
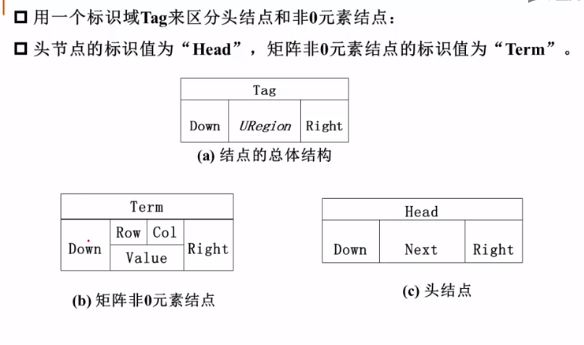
多重链表
多重链表:链表中的节点可能同时隶属于多个链
- 多重链表中结点的指针域会有多个,如前面例子包含了Next和SubList两个指针域
- 但包含两个指针域的链表并不一定是多重链表,比如双向链表不是多重链表
- 多重链表有广泛的用途:基本上如树,图这样相对复杂的数据结构都可以采用多重链表方式实现存储
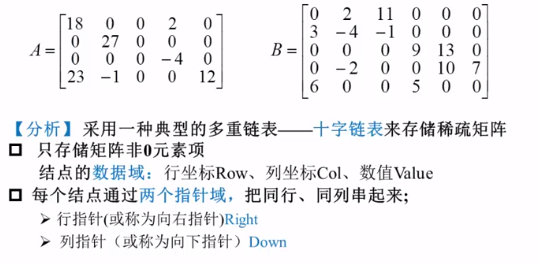
【例】矩阵可以用二维数组表示,但二维数组表示有两个缺陷:
- 数组的大小需要事先确定
- 对于“稀疏矩阵”(0很多的矩阵),将造成大量的存储空间浪费
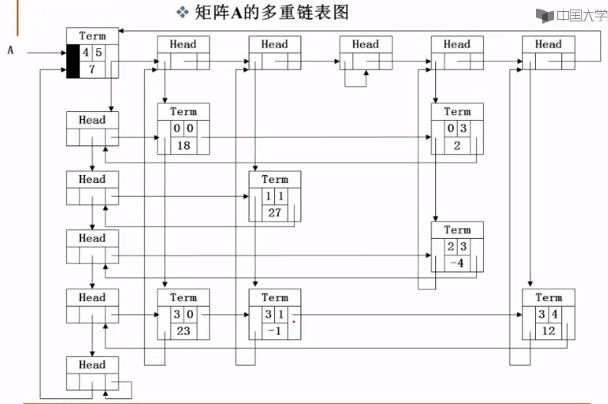
矩阵A的多重链表图














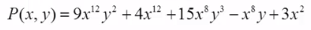

















 2938
2938

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








