【算法】FFT-快速傅里叶变换

FFT作用

FFT在算法竞赛中就有一个用途：加速多项式乘法

多项式：形如 $a_0{X}^0+a_1{X}^1+......+a_n{X}^n$ 的代数表达式，可以记作$f(X)=a_0{X}^0+a_1{X}^1+......+a_n{X}^n$，其中，$a_0,a_1,a_2,......,a_n$ 是多项式的系数。

如果有两个多项式 $f(X),g(X)$ ，要求这两个多项式的乘积。那么最朴素的做法是每一位相乘，时间复杂度是$O(n^2)$，很多情况下，需要优化，所以，就出现了FFT，时间复杂度是$O(nlogn)$

数学知识

多项式，复数，单位根，多项式的系数表达法，多项式的点值表达法…
有亿点点复杂，给一个链接，自己能理解多少就理解多少吧。
详解

代码：

其实FFT就是多项式的系数表示法与点值表示法之间的互换。
系数表达法容易用公式表示，但是相乘不容易；点值表示法相乘容易，不方便表示。
（点值表示法相乘：两个多项式P,Q分别取点$(x,y_1)和(x,y_2)$ ，$P\ast Q$ 就是点$(x,y1\ast y2)$ ,所以$P\ast Q$ 的多项式的点值表示法就是$(x,y1\ast y2)$）
type=1：系数表示法 ——> 点值表示法
type=-1：点值表示法 ——> 系数表示法

例题1：多项式乘法

P3803 多项式乘法

题目：


代码：

#include <cstdio>
#include <cmath>
#include <iostream> 
using namespace std;
const int maxn=4*1e6+10;
const double pi=acos(-1.0);
struct Complex
{
    double x, y;
    Complex(double x=0,double y=0):x(x),y(y){}
    Complex operator+(const Complex &W) const
    {
        return {x + W.x, y + W.y};
    }
    Complex operator-(const Complex &W) const
    {
        return {x - W.x, y - W.y};
    }
    Complex operator*(const Complex &W) const
    {
        return {x * W.x - y * W.y, x * W.y + y * W.x};
    }
};
//a[i]表示当x=单位根的i次方时y的值 
Complex a[maxn],b[maxn];
int rev[maxn],n,m;
int l=1,bit=0;

void inif(int num)//l为位数,rev[i]代表i的位逆序置换操作后的结果 
{
	l=1,bit=0;
	while(l<=num) 
		l<<=1,bit++;
	for(int i=1;i<(1<<bit);i++)
		rev[i]=(rev[i>>1]>>1)|((1&i)<<bit-1);
}
void fft(Complex *f,int len,int type)
{
	for(int i=1;i<len;i++)
		if(rev[i]>i) swap(f[rev[i]],f[i]);
	for(int l=2;l<=len;l<<=1)//区间长度 
	{
		Complex wn=(Complex){cos(2*pi/l),type*sin(2*pi/l)};	//单位根 
		for(int i=0;i+l<=len;i+=l)
		{
			Complex w=(Complex){1,0};//幂 
			for(int k=i;k<i+(l>>1);k++,w=w*wn)
			{
				Complex t=w*f[k+(l>>1)],tmp=f[k];
				f[k]=tmp+t;//蝴蝶效应 
				f[k+(l>>1)]=tmp-t;
			}
		}
	}	
	if(type==-1)
	{
		for(int i=0;i<=n+m;i++) 
			f[i].x=(int)(f[i].x/l+0.5);
	}		 
}

int main ()
{
	scanf("%d%d",&n,&m);
	for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
	for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
	inif(n+m);
	fft(a,l,1); fft(b,l,1);//l是多项式项数
	for(int i=0;i<l;i++) a[i]=a[i]*b[i];
	fft(a,l,-1);
	for(int i=0;i<=n+m;i++) printf("%d ",(int)a[i].x);

	return 0;
}

例题2：大数相乘

P1919 A*B Problem升级版

题目：


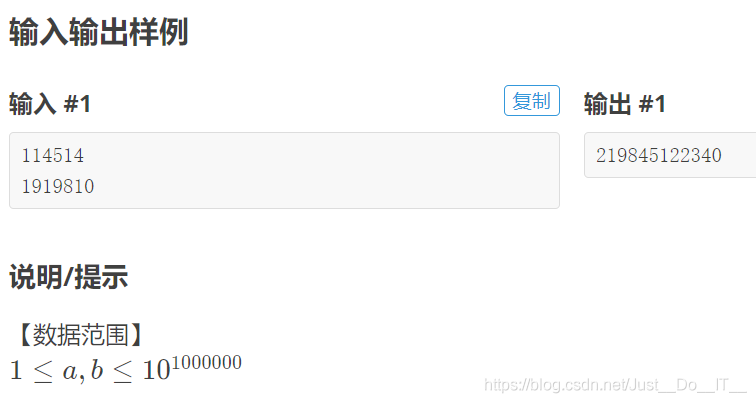
解题思路：

对于每一个 n 位的十进制数，我们可以看做一个 n-1 次多项式 A，满足

$A(x)=a_0+a_1\times 10+a_2\times 10^2+\cdots +a_{n-1}\times 10^{n-1}$

那么对于两个大整数相乘,我们就可以卷起来辣！

小细节：

1. 首先要将读进去的大整数逆序存入多项式的系数中
2. 计算出相乘后的系数，别忘记处理进位问题

代码：

#include <cstdio>
#include <cmath>
#include <iostream> 
using namespace std;
const int maxn=4e6+10;
const double pi=acos(-1.0);
struct Complex
{
    double x, y;
    Complex(double x=0,double y=0):x(x),y(y){}
    Complex operator+(const Complex &W) const
    {
        return {x + W.x, y + W.y};
    }
    Complex operator-(const Complex &W) const
    {
        return {x - W.x, y - W.y};
    }
    Complex operator*(const Complex &W) const
    {
        return {x * W.x - y * W.y, x * W.y + y * W.x};
    }
};
Complex a[maxn],b[maxn];
int ans[maxn];
int rev[maxn],n,m;
int l=1,bit=0;

void inif(int num)
{
	l=1,bit=0;
	while(l<=num) 
		l<<=1,bit++;
	for(int i=0;i<(1<<bit);i++)
		rev[i]=(rev[i>>1]>>1)|((1&i)<<bit-1);
}
void fft(Complex *f,int len,int type)
{
	for(int i=0;i<len;i++)
		if(rev[i]>i) swap(f[rev[i]],f[i]);
	for(int l=2;l<=len;l<<=1) 
	{
		Complex wn=(Complex){cos(2*pi/l),type*sin(2*pi/l)};	
		for(int i=0;i+l<=len;i+=l)
		{
			Complex w=(Complex){1,0};
			for(int k=i;k<i+(l>>1);k++,w=w*wn)
			{
				Complex t=w*f[k+(l>>1)],tmp=f[k];
				f[k]=tmp+t;
				f[k+(l>>1)]=tmp-t;
			}
		}
	}	
	if(type==-1)
	{
		for(int i=0;i<=len;i++) 
			f[i].x=(int)(f[i].x/len+0.5);
	}		 
}


int main ()
{
	string s1,s2;
	cin>>s1>>s2;
	n=s1.size();
	n--;
	m=s2.size();
	m--;
	for(int i=0;i<=n;i++) //逆序存储 
		a[i].x=s1[n-i]-'0';
	for(int i=0;i<=m;i++) 
		b[i].x=s2[m-i]-'0';
	inif(n+m);
	fft(a,l,1); fft(b,l,1);
	for(int i=0;i<l;i++) a[i]=a[i]*b[i];
	fft(a,l,-1);
	for(int i=0;i<l;i++) //进位处理 
	{
		ans[i]+=a[i].x;
		if(ans[i]>=10)
		{
			ans[i+1]+=(ans[i]/10);
			ans[i]%=10;
		}
	}
	int pos=l;//从l开始找第一位不是0的数字 
	while(!ans[pos] && pos>0)	pos--;
	for(int i=pos;i>=0;i--)
		printf("%d",ans[i]);
	return 0;
}

碎碎念：

这个FFT，我只会用，但是对于背后神奇的数学推导，一知半解…