Leetcode（77）——组合

最新推荐文章于 2023-09-08 16:23:54 发布

SmileGuy17

最新推荐文章于 2023-09-08 16:23:54 发布

阅读量579

点赞数 1

分类专栏： Leetcode 文章标签： leetcode 深度优先算法

本文链接：https://blog.csdn.net/KCDCY/article/details/125656584

版权

Leetcode 专栏收录该内容

77 篇文章 6 订阅

订阅专栏

Leetcode（77）——组合

题目

给定两个整数 n 和 k，返回范围 $[1, n]$ 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

$1$ <= n <= $20$
$1$ <= k <= $n$

题解

方法一：回溯法

思路

类似于排列问题，比如 Leetcode.46.全排列，我们也可以进行回溯。但是 排列回溯的是交换的位置，而组合回溯的是是否把当前的数字加入结果中。
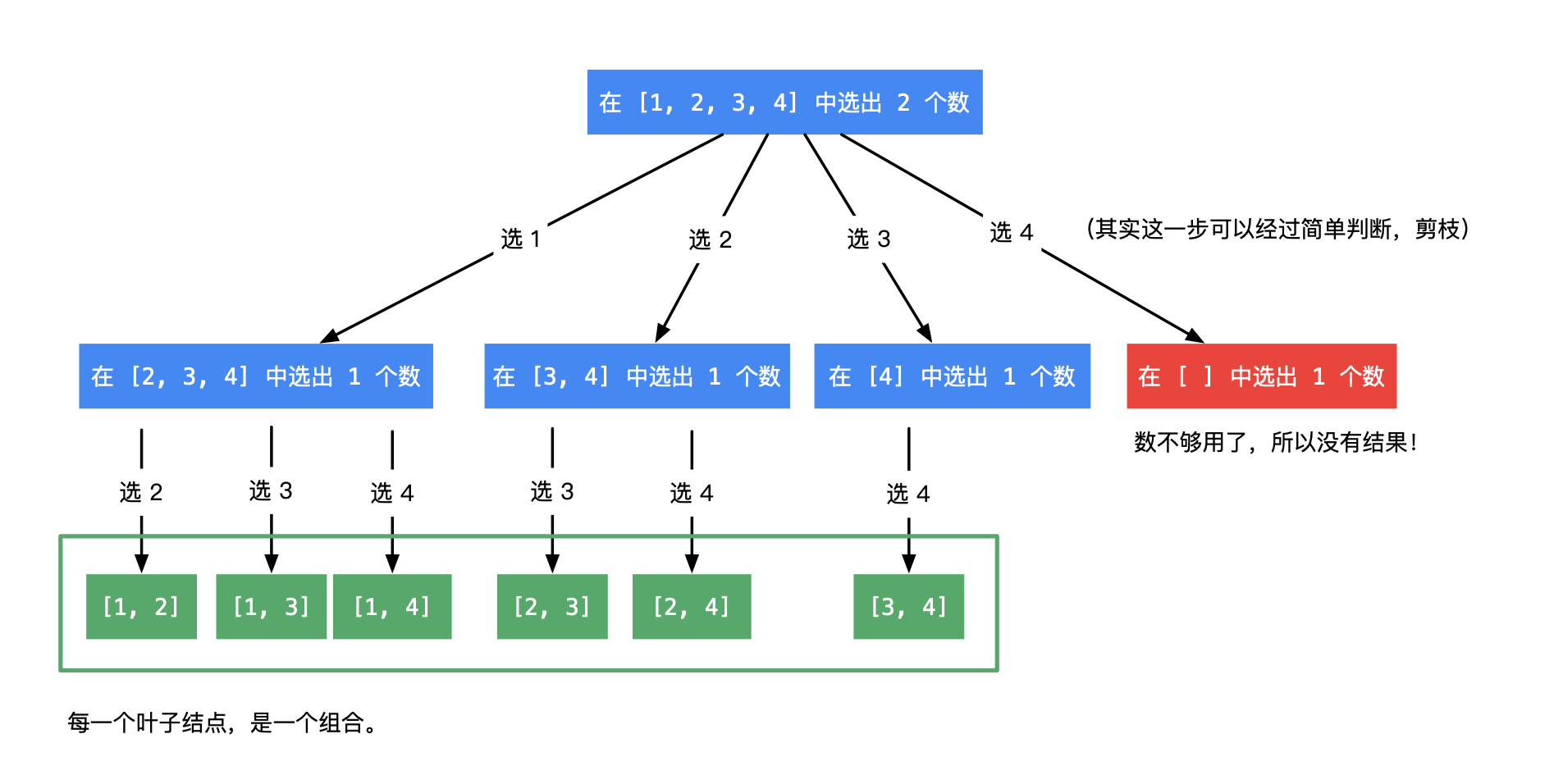
在这里插入图片描述
在这里我们还是用了剪枝以优化算法，从而减小时间复杂度——通过剪去无意义的遍历和递归。

如果当前 $\textit{nums}$ 的大小为 $s$ ，未确定状态的区间 $[\textit{cur}, n]$ 的长度为 $t$ ，如果 $s + t < k$ ，那么即使 $t$ 个都被选中，也不可能构造出一个长度为 $k$ 的序列，故这种情况就没有必要继续向下递归——即我们可以在每次递归开始的时候做一次这样的判断。

下面的图片绿色部分是剪掉的枝叶，当 $n$ 很大的时候，能少遍历很多结点，节约了时间。
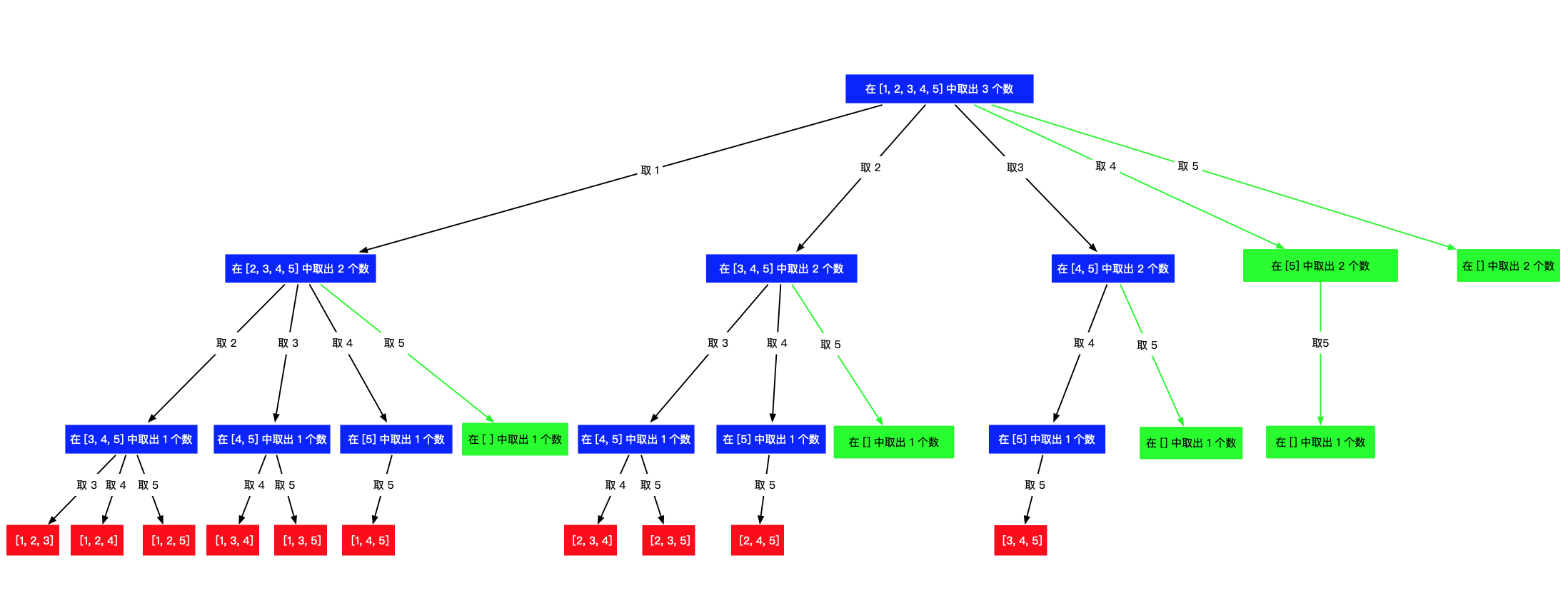
在这里插入图片描述

代码实现

Leetcode 官方题解：

class Solution {
public:
    vector<int> temp;
    vector<vector<int>> ans;

    void dfs(int cur, int n, int k) {
        // 剪枝：temp 长度加上区间 [cur, n] 的长度小于 k，不可能构造出长度为 k 的 temp
        if (temp.size() + (n - cur + 1) < k) {
            return;
        }
        // 记录合法的答案
        if (temp.size() == k) {
            ans.push_back(temp);
            return;
        }
        // 考虑选择当前位置
        temp.push_back(cur);
        dfs(cur + 1, n, k);
        temp.pop_back();
        // 考虑不选择当前位置
        dfs(cur + 1, n, k);
    }

    vector<vector<int>> combine(int n, int k) {
        dfs(1, n, k);
        return ans;
    }
};

我自己的：

// 初始版本
class Solution {
    vector<int> nums;
    vector<vector<int>> ans;
    void DFS(int k, int n, int first){
        if(k == nums.size()){
            ans.emplace_back(nums);
        }else{
            for(int i = first; i <= n; i++){
                nums.push_back(i);
                DFS(k, n, i+1);
                nums.pop_back();
            }
        }
    }
public:
    vector<vector<int>> combine(int n, int k){
        // [1, n] 中的 C{k_n}
        int last = n+1-k;
        DFS(k, n, 1);
        return ans;
    }
};

// 改进后（剪枝法）
class Solution {
    vector<int> nums;
    vector<vector<int>> ans;
    void DFS(int k, int n, int first){
        if(k-nums.size() > n-first+1) return;   // 剪枝
        if(k == nums.size()){
            ans.emplace_back(nums);
        }else{
            for(int i = first; i <= n; i++){
                nums.push_back(i);
                DFS(k, n, i+1);
                nums.pop_back();
            }
        }
    }
public:
    vector<vector<int>> combine(int n, int k){
        // [1, n] 中的 C{k_n}
        int last = n+1-k;
        DFS(k, n, 1);
        return ans;
    }
};

复杂度分析

时间复杂度： $\choose k} \times k)$
空间复杂度： $O (n + k) = O (n)$ ，因为 $n > = k$ ，即递归使用栈空间的空间代价和临时数组 $\textit{nums}$ 的空间代价。

方法二：非递归（字典序法）实现组合型枚举

思路

这里的非递归版不是简单的用栈模拟递归转化为非递归：我们希望通过合适的手段，消除递归栈带来的额外空间代价。

假设我们把原序列中被选中的位置记为 $1$ ，不被选中的位置记为 $0$ ，对于每个方案都可以构造出一个二进制数。我们让原序列从大到小排列（即 $\{ n, n - 1, \cdots 1, 0 \}$ ）。我们先看一看 $n = 4$ ， $k = 2$ 的例子：
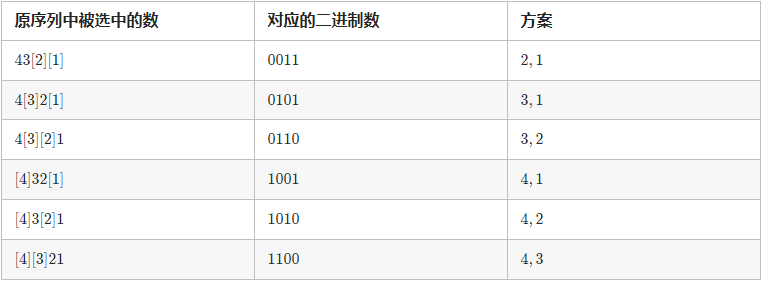
在这里插入图片描述
我们可以看出 「对应的二进制数」一列包含了由 $k$ 个 $1$ 和 $n - k$ 个 $0$ 组成的所有二进制数，并且它们按照字典序排列。这给了我们一些启发，我们可以通过某种方法枚举，使得生成的序列是根据字典序递增的。我们可以考虑有一个二进制数数字 $x$ ，它由 $k$ 个 $1$ 和 $n - k$ 个 $0$ 组成，如何找到它的字典序中的下一个数字 ${next}(x)$ 呢？这里分两种情况：

规则一： $x$ 的最低位为 $1$ ，这种情况下，如果末尾由 $t$ 个连续的 $1$ ，我们直接将倒数第 $t$ 位的 $1$ 和倒数第 $t + 1$ 位的 $0$ 替换，就可以得到 ${next}(x)$ 。如 $\rightarrow 0101$ ， $\rightarrow 0110$ ， $\rightarrow 1010$ ， $\rightarrow 1010111$ 。
规则二： $x$ 的最低位为 $0$ ，这种情况下，末尾有 $t$ 个连续的 $0$ ，而这 $t$ 个连续的 $0$ 之前有 $m$ 个连续的 $1$ ，我们可以将倒数第 $t + m$ 位置的 $1$ 和倒数第 $t + m + 1$ 位的 $0$ 对换，然后把倒数第 $t + 1$ 位到倒数第 $t + m - 1$ 位的 $1$ 移动到最低位。如 $\rightarrow 1001$ ， $\rightarrow 1100$ ， $\rightarrow 1100011$ 。

至此，我们可以写出一个简单的算法，用一个长度为 $n$ 的 $0 / 1$ 数组来表示选择方案对应的二进制数，初始状态下最低的 $k$ 位全部为 $1$ ，其余位置全部为 $0$ ，然后不断通过上述方案求 $n e x t$ ，就可以构造出所有的方案。
$— — — — 接下来将进一步优化算法 — — — —$

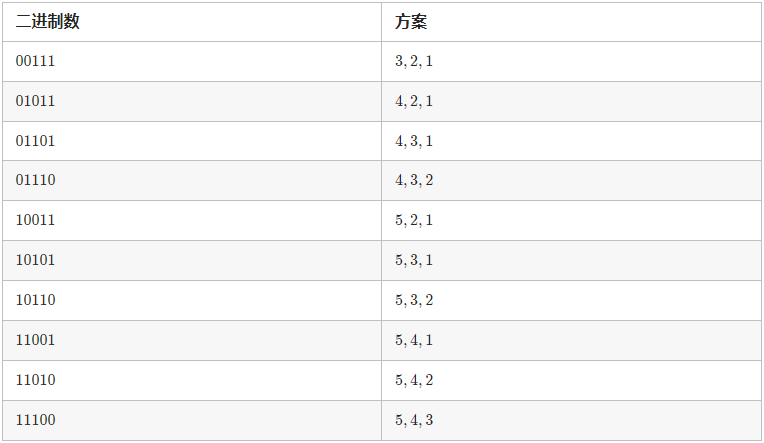
我们可以进一步优化实现，我们来看 $n = 5$ ， $k = 3$ 的例子，根据上面的策略我们可以得到这张表：
在这里插入图片描述
在上面的方法中我们通过二进制数来构造方案，而二进制数是需要通过迭代的方法来获取 $n e x t$ 的。

现在考虑不通过二进制数，直接在方案上变换来得到下一个方案。假设一个方案从低到高的 $k$ 个数分别是 $\{ a_0, a_1, \cdots, a_{k - 1} \}$ ，我们可以从低位向高位找到第一个 $j$ 使得 $a_{j} + 1 \neq a_{j + 1}$ ，我们知道出现在 $a$ 序列中的数字在二进制数中对应的位置一定是 $1$ ，即表示被选中，那么 $a_{j} + 1 \neq a_{j + 1}$ 意味着 $a_j$ 和 $a_{j + 1}$ 对应的二进制位中间有 $0$ ，即这两个 $1$ 不连续。此时我们把 $a_j$ 对应的 $1$ 向高位推送，也就对应着 $a_j \leftarrow a_j + 1$ ，而对于 $\in [0, j - 1]$ 内所有的 $a_i$ 把值恢复成 $i + 1$ ，即对应这 $j$ 个 $1$ 被移动到了二进制数的最低 $j$ 位。
这似乎只考虑了上面的「规则二」。但是实际上 「规则一」是「规则二」在 $t = 0$ 时的特殊情况，因此这么做和按照两条规则模拟是等价的。

在实现的时候，我们可以用一个数组 $\textit{temp}$ 来存放 $a$ 序列，一开始我们先把 $1$ 到 $k$ 按顺序存入这个数组，他们对应的下标是 $0$ 到 $k - 1$ 。为了计算的方便，我们需要在下标 $k$ 的位置放置一个哨兵 $n + 1$ （思考题：为什么是 $n + 1$ 呢？）。然后对这个 $\textit{temp}$ 序列按照这个规则进行变换，每次把前 $k$ 位（即除了最后一位哨兵）的元素形成的子数组加入答案。每次变换的时候，我们把第一个 $a_{j} + 1 \neq a_{j + 1}$ 的 $j$ 找出，使 $a_j$ 自增 $1$ ，同时对 $\in [0, j - 1]$ 的 $a_i$ 重新置数。如此循环，直到 $\textit{temp}$ 中的所有元素为 $n$ 内最大的 $k$ 个元素。

思考题：为什么是 $n + 1$ 呢？
回过头看这个思考题，它是为了我们判断退出条件服务的。我们如何判断枚举到了终止条件呢？其实不是直接通过 $\textit{temp}$ 来判断的，我们会看每次找到的 $j$ 的位置，如果 $j = k$ 了，就说明 $[0, k - 1]$ 内的所有的数字是比第 $k$ 位小的最后 $k$ 个数字，这个时候我们找不到任何方案的 $k$ 位序列的字典序比当前方案的序列大了，此时结束枚举。

代码实现

Leetcode 官方题解：

class Solution {
public:
    vector<int> temp;
    vector<vector<int>> ans;

    vector<vector<int>> combine(int n, int k) {
        // 初始化
        // 将 temp 中 [0, k - 1] 每个位置 i 设置为 i + 1，即 [0, k - 1] 存 [1, k]
        // 末尾加一位 n + 1 作为哨兵
        for (int i = 1; i <= k; ++i) {
            temp.push_back(i);
        }
        temp.push_back(n + 1);
        
        int j = 0;
        while (j < k) {
            ans.emplace_back(temp.begin(), temp.begin() + k);
            j = 0;
            // 寻找第一个 temp[j] + 1 != temp[j + 1] 的位置 t
            // 我们需要把 [0, t - 1] 区间内的每个位置重置成 [1, t]
            while (j < k && temp[j] + 1 == temp[j + 1]) {
                temp[j] = j + 1;
                ++j;
            }
            // j 是第一个 temp[j] + 1 != temp[j + 1] 的位置
            ++temp[j];
        }
        return ans;
    }
};

我自己的：

class Solution {
public:
    vector<int> nums;
    vector<vector<int>> ans;

    vector<vector<int>> combine(int n, int k){
        // 初始化
        for(int i = 1; i <= k; ++i)
            nums.push_back(i);
        nums.push_back(n + 1);  // 哨兵
        int j = 0;
        while(j < k){
            // 插入新序列
            ans.emplace_back(nums.begin(), nums.end()-1);
            // 更新新序列
            // 找到第一个 nums_j + 1 != nums_{j+1} 的数，并在二进制数中将对应的位数至 nums_{j+1} 对应的位数交换
            // 即在序列 nums 中令 nums_j = nums_j + 1
            // 并令序列中 nums_i 属于 [0, j-1] 的 nums_i = i+1
            for(j = 0; j < k; j++){
                if(nums[j]+1 != nums[j+1]) break;
                else nums[j] = j+1;
            }
            nums[j] = nums[j]+1;
        }
        return ans;
    }
};

复杂度分析

时间复杂度： $\choose k} \times k)$ 。外层循环的执行次数是 $\choose k$ 次，每次需要做一个 $O (k)$ 的添加答案和 $O (k)$ 的内层循环，故时间复杂度 $\choose k} \times k)$ 。
空间复杂度： $O (k)$ 。即辅助数组 $\textit{temp}$ 的空间代价。