scipy短时傅里叶分析
基本原理:
为了使STFT能够通过STFT逆变换反变换,信号加窗必须服从“非零重叠加”(NOLA)的约束,输入信号必须具有完整的加窗覆盖即
(
x
.
s
h
a
p
e
[
a
x
i
s
]
−
n
p
e
r
s
e
g
)
(x.shape[axis] - nperseg) % (nperseg-noverlap) == 0
(x.shape[axis]−nperseg)。可以使用更高级的填充参数来完成这一任务。
给出了时域信号
x
[
n
]
x[n]
x[n]、窗口
w
[
n
]
w[n]
w[n]和hop size
H
=
n
p
e
r
s
e
g
−
n
o
v
e
r
l
p
H=nperseg-noverlp
H=nperseg−noverlp时,时间指数t处的加窗帧:
X
t
[
n
]
=
x
[
n
]
w
[
n
−
t
H
]
X_t[n]=x[n]w[n−tH]
Xt[n]=x[n]w[n−tH]
给出了重叠-加法(OLA)重建方程。
X
[
n
]
=
∑
t
x
t
[
n
]
w
[
n
−
t
H
]
∑
t
w
2
[
n
−
t
H
]
X[n]=\frac{∑_tx_t[n]w[n−tH]}{∑_tw^2[n−tH]}
X[n]=∑tw2[n−tH]∑txt[n]w[n−tH]
NOLA约束确保OLA重建方程分母中出现的每一个归一化项都是非零的。通过CHECK_NOLA可以检验是否可以选择满足该约束条件的窗口、非标准窗口和非标准节点。
接口:
scipy.signal.stft(x, fs=1.0, window='hann', nperseg=256, noverlap=None, nfft=None, detrend=False, return_onesided=True, boundary='zeros', padded=True, axis=- 1, scaling='spectrum')
"""
Compute the Short Time Fourier Transform (STFT).
STFTs can be used as a way of quantifying the change of a nonstationary signal’s frequency and phase content over time.
STFT可以用来量化非平稳信号的频率和相位随时间的变化。
Parameters
x:array_like
Time series of measurement values
测量值的时间序列
fs:float, optional
Sampling frequency of the x time series. Defaults to 1.0.
x时间序列的采样频率
window:str or tuple or array_like, optional
Desired window to use. If window is a string or tuple, it is passed to get_window to generate the window values, which are DFT-even by default. See get_window for a list of windows and required parameters. If window is array_like it will be used directly as the window and its length must be nperseg. Defaults to a Hann window.
需要使用的窗口。如果window是一个字符串或元组,它将被传递给get_windows以生成窗口值,这些值在默认情况下是DFT-even。有关窗口和所需参数的列表,请参阅get_window。如果window是array_like,它将直接作为窗口使用,并且它的长度必须是nperseg。默认为Hann窗口。
nperseg:int, optional
Length of each segment. Defaults to 256.
每个段的长度。默认值为256。
noverlap:int, optional
Number of points to overlap between segments. If None, noverlap = nperseg // 2. Defaults to None. When specified, the COLA constraint must be met (see Notes below).
段之间要重叠的点数。如果没有,则noverlap=nperseg//2。默认为无。指定后,必须满足COLA约束(见注释)
nfft:int, optional
Length of the FFT used, if a zero padded FFT is desired. If None, the FFT length is nperseg. Defaults to None.
如果需要零填充FFT,则使用的FFT长度。如果无,则FFT长度为nperseg。默认为无。
detrend:str or function or False, optional
Specifies how to detrend each segment. If detrend is a string, it is passed as the type argument to the detrend function. If it is a function, it takes a segment and returns a detrended segment. If detrend is False, no detrending is done. Defaults to False.
指定如何去除每个段的趋势。如果dettrend是一个字符串,那么它将作为类型参数传递给detrend函数。如果它是一个函数,它接受一个段并返回一个去趋势段。如果去趋势为False,则不进行去趋势。默认值为False。
return_onesided:bool, optional
If True, return a one-sided spectrum for real data. If False return a two-sided spectrum. Defaults to True, but for complex data, a two-sided spectrum is always returned.
如果为真,则返回真实数据的单侧频谱。如果False返回一个双边频谱。默认为True,但是对于复杂的数据,总是返回双面频谱。
boundary:str or None, optional
Specifies whether the input signal is extended at both ends, and how to generate the new values, in order to center the first windowed segment on the first input point. This has the benefit of enabling reconstruction of the first input point when the employed window function starts at zero. Valid options are ['even', 'odd', 'constant', 'zeros', None]. Defaults to ‘zeros’, for zero padding extension. I.e. [1, 2, 3, 4] is extended to [0, 1, 2, 3, 4, 0] for nperseg=3.
指定输入信号是否在两端扩展,以及如何生成新值,以便将第一个窗口段居中于第一输入点。这样做的好处是,当所采用的窗口函数从零开始时,能够重建第一个输入点。有效的选项是【偶数,奇数,常数,零,无】。对于零填充扩展,默认为“零”。也就是说,对于nperseg=3的情况,【1,2,3,4】被扩展到了【0,1,2,3,4,0】的情况下,当n=3时,我们将得到一个很好的结果。
padded:bool, optional
Specifies whether the input signal is zero-padded at the end to make the signal fit exactly into an integer number of window segments, so that all of the signal is included in the output. Defaults to True. Padding occurs after boundary extension, if boundary is not None, and padded is True, as is the default.
指定是否在输入信号的末尾添加零填充,以使信号精确地适合于整数个窗口段,从而使所有信号都包含在输出中。默认为“真”。如果边界不为“无”,则在边界扩展之后进行填充,并且填充为“真”,这是默认设置。
axis:int, optional
Axis along which the STFT is computed; the default is over the last axis (i.e. axis=-1).
计算STFT的轴;默认值位于最后一个轴上(即轴=-1)。
scaling: {‘spectrum’, ‘psd’}
The default ‘spectrum’ scaling allows each frequency line of Zxx to be interpreted as a magnitude spectrum. The ‘psd’ option scales each line to a power spectral density - it allows to calculate the signal’s energy by numerically integrating over abs(Zxx)**2.
默认的“频谱”缩放允许Zxx的每个频率线被解释为幅度频谱。“psd”选项将每一行缩放到一个功率谱密度——它允许通过对abs(Zxx)**2的数值积分来计算信号的能量。
Returns
f:ndarray
Array of sample frequencies.
采样频率阵列。
t:ndarray
Array of segment times.
段时间的数组。
Zxx:ndarray
STFT of x. By default, the last axis of Zxx corresponds to the segment times.
x的短时傅立叶变换。默认情况下,Zxx的最后一个轴对应于分段时间。
"""
示例:
from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
rng = np.random.default_rng()
#Generate a test signal, a 2 Vrms sine wave whose frequency is slowly modulated around 3kHz
# , corrupted by white noise of exponentially decreasing magnitude sampled at 10 kHz.
fs = 10e3
N = 1e5
amp = 2 * np.sqrt(2)
noise_power = 0.01 * fs / 2
time = np.arange(N) / float(fs)
mod = 500*np.cos(2*np.pi*0.25*time)
carrier = amp * np.sin(2*np.pi*3e3*time + mod)
noise = rng.normal(scale=np.sqrt(noise_power),
size=time.shape)
noise *= np.exp(-time/5)
x = carrier + noise
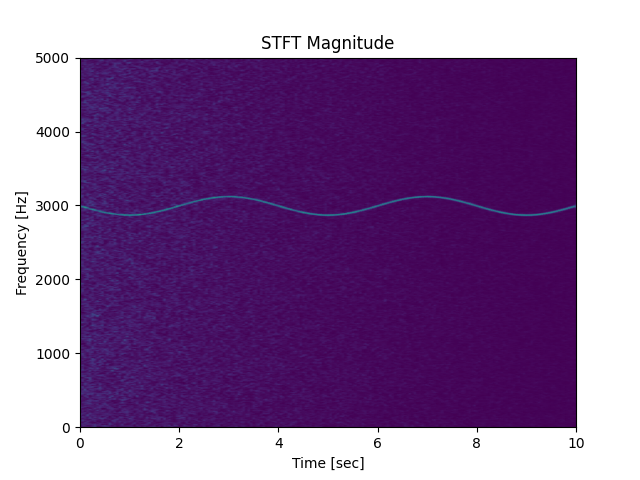
# Compute and plot the STFT’s magnitude.
f, t, Zxx = signal.stft(x, fs, nperseg=1000)
plt.pcolormesh(t, f, np.abs(Zxx), vmin=0, vmax=amp, shading='gouraud')
plt.title('STFT Magnitude')
plt.ylabel('Frequency [Hz]')
plt.xlabel('Time [sec]')
plt.show()
引用:
[^1] :scipy.signal.stft — SciPy v1.9.3 Manual
[^2] :Oppenheim, Alan V., Ronald W. Schafer, John R. Buck “Discrete-Time Signal Processing”, Prentice Hall, 1999.
scipy.signal.stft)
[^3] :Daniel W. Griffin, Jae S. Lim “Signal Estimation from Modified Short-Time Fourier Transform”, IEEE 1984, 10.1109/TASSP.1984.1164317























 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










