动态规划基础

本文来自于《算法导论》第二版第十五章动态规划部分的读书笔记。

理论部分

• 动态规划技术所适用的问题是什么？

  Dynamic Programming typically applies to optimization problems in which a set of choices must be made in order to arrive at an optimal solution.

  我的理解：动态规划主要用来解决最优化问题，并且是需要多阶段决策的。
  As choices are made, sub-problems of the same form often arise.Dynamic Programming is effective when a given sub-problem may arise from more than one partial set of choices.the key technique is to store the solution to each such sub-problem in case it should reappear.

  我的理解：这一部分其实说明DP技术的基础其实是divide and conquer，也是不断的切分原问题为子问题，后者与原问题有同样的形式。并且，同一子问题是会反复出现的，在决策的过程中可能会多次产生同样的子问题，所以DP技术通过存储每个子问题的解，来使算法变得高效。

• 什么时候用动态规划( Elements of dynamic programming )

  Optimal Substructure
  An optimal solution to a problem contains within it an optimal solution to sub-problems.We refer to this property as optimal substructure.Whenever a problem exhibits optimal substructure. It is a good clue that dynamic programming might apply.

  我的理解：本段说了DP适用问题的第一个特点，就是原问题的解结构具有最优子结构的性质，这种形式是说原文题的最优解内含了子问题的最优解。

  Overlapping Problems
  Dynamic Programming is applicable when the sub-problems are not independent, that is , when sub-problems share sub-problems.When a recursive algorithm revisits the same problem over and over again, we say that the optimization problem has overlapping sub-problems.

  我的理解：这一部分讲了DP适用问题的第二个特点，这个角度是从问题去说的，上面的角度是从解的结构去说的。即在递归的过程中贡献子问题的时候，那么就会出现对于同一问题的重复求解。DP通过保留子问题解的方法，避免了这种情形的发生。

• 动态规划的解题步骤(Steps of dynamic programming)

  1. Characterize the structure of an optimal solution
  2. Recursively define the value of an optimal solution
  3. Compute the value of an optimal solution in a bottom-up fashion.
  4. Construct an optimal solution from computed information.

  我的理解：
  通常情况下第一步应该是判断原问题是否满足DP使用的条件，主要是分析是否具有最优子结构。如果具有最优子结构，那么可以按照如下步骤：
  1.状态定义(每个阶段子问题最优解)
  2.转移函数
  3.初始化
  4.自底向上求解

问题

To find the fastest way through a factory.
这个问题我简述下：
一个产品的出场要经过多道工序的加工方可出场。某工厂有两条工作线，每条工作线都具有n道工序。并且对应位置的工序执行相同的操作，但是他们具有不同的时间代价。在同一条工作线当中，由当前工序转移到下一道工序是没有时间代价的，但是从不同的工做线转移是具有时间代价的。

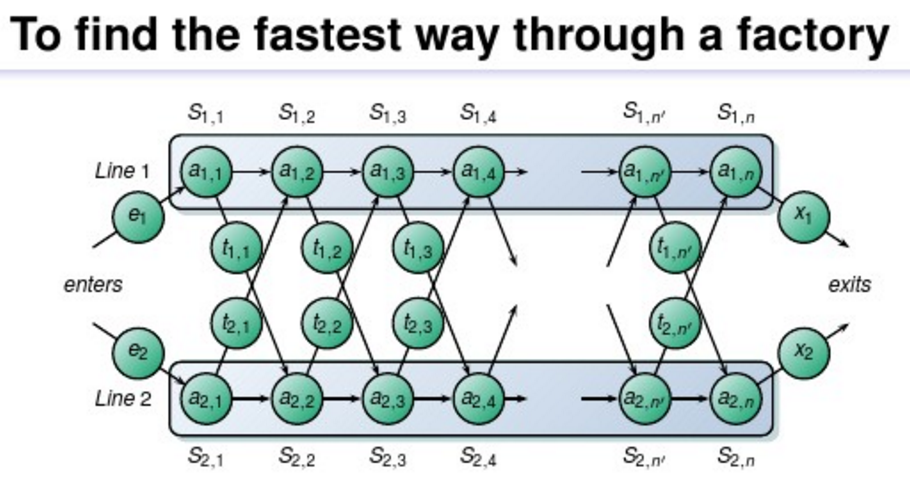
现在的问题就是：给出每条工作线各个工序的时间代价，以及不同工作线工序互相转移的时间代价。求出一个产品出厂前所要经历的最短时间。如下图所示：

分析

首先，分析原问题解的结构。

假设，$S_{1,j}$是原问题最优解所经历的工序，当$S_{1,j}$来自于$S_{1,j-1}$时，$S_{1,j-1}$一定也是原问题最优解所经历的工序。即$S_{1,j}$是最快的，而它又来自于$S_{1,j-1}$，那么$S_{1,j-1}$也一定是最快的。否则，如果到达$S_{1,j-1}$不是最快的，那么我们用更快的那条路到达$S_{1,j}$，则这条路是要比原来那条路更快的，而这与假设$S_{1,j}$是最快的互相矛盾。所以，如果即$S_{1,j}$是最快的，而它又来自于$S_{1,j-1}$，那么$S_{1,j-1}$也一定是最快的。

所以，有如下的结论：
The fastest way through station $S_{1,j}$, is either

• The fastest way through station $S_{1,j-1}$ or,
• The fastest way through station $S_{2,j-1}$

同样的，
The fastest way through station $S_{2,j}$, is either

• The fastest way through station $S_{1,j-1}$ or,
• The fastest way through station $S_{2,j-1}$

那么，由对原问题的分析，我们可以定义如下的最优函数，以及转移函数
Let $f_{i}[j]$ denote the fastest possible time through station $S_{i,j}$

最优函数：

$$f^{*} = min( f_{1}[n] + x_{1} , f_{2}[n] + x_{2} )\tag{1}$$
转移函数：
$$f_{1}[j]=\left\{ \begin{aligned} e_{1} + a_{1,1} , &&j = 1 \\ \min( f_{1}[j-1] + a_{1,j} \quad,\quad f_{2}[j-1] + t_{2,j-1} + a_{1,j} ), && j > 1 \\ \end{aligned} \right. \tag{2}$$
$$f_{2}[j]=\left\{ \begin{aligned} e_{2} + a_{2,1} , &&j = 1 \\ \min( f_{1}[j-1] +t_{1,j-1} + a_{2,j} \quad,\quad f_{2}[j-1] + a_{2,j} ), && j > 1 \\ \end{aligned} \right. \tag{3}$$

代码

#include <iostream>
#include <fstream>
#define LOCAL
const int maxn = 32;

int s1[maxn]; // station1[j]
int s2[maxn]; // station2[j]

int t1[maxn]; // time cost of s1[j-1] to s2[j]
int t2[maxn]; // time cost of s2[j-1] to s1[j]

int dp1[maxn]; // fastest path through s1[j]
int dp2[maxn]; // fastest path through s2[j]

int flag1[maxn]; // which line from [j-1] to s1[j]
int flag2[maxn]; // which line from [h-1] to s2[j]

int ans[maxn];

int main()
{
#ifdef LOCAL
    std::ifstream cin( "input.dat" );
    std::ofstream cout( "output.dat" );
#endif
    int n = 0;
    while( cin >> n )
    {
        int e1, x1;
        int e2, x2;
        cin >> e1 >> x1;
        cin >> e2 >> x2;

        for( int i = 0; i < n; ++i )
            cin >> s1[i];
        for( int i = 0; i < n; ++i )
            cin >> s2[i];
        for( int i = 0; i < n-1; ++i )
            cin >> t1[i];
        for( int i = 0; i < n-1; ++i )
            cin >> t2[i];

        dp1[0] = e1 + s1[0];
        dp2[0] = e2 + s2[0];
        flag1[0] = 1;
        flag2[0] = 2;

        for( int j = 1; j < n; ++j )
        {
            // 处理第一条流水线
            if( dp1[j-1] < dp2[j-1] + t2[j-1] )
            {
                flag1[j] = 1;
                dp1[j] = dp1[j-1] + s1[j]; 
            }
            else
            {
                flag1[j] = 2;
                dp1[j] = dp2[j-1] + t2[j-1] + s1[j]; 
            }

            // 处理第二条流水线
            if( dp2[j-1] < dp1[j-1] + t1[j-1] )
            {
                flag2[j] = 2;
                dp2[j] = dp2[j-1] + s2[j]; 
            }
            else
            {
                flag2[j] = 1;
                dp2[j] = dp1[j-1] + t1[j-1] + s2[j]; 
            }
        }

        int first = dp1[n-1] + x1;
        int second = dp2[n-1] + x2;
        int result = ( first < second )?first:second;
        cout << result << std::endl;

        // 寻找最优路径的station
        if( first < second )
            ans[n-1] = 1;
        else
            ans[n-1] = 2;

        for( int i = n-2 ; i >= 0; --i )
        {
            if( ans[i + 1] == 1 ) // 对流水线进行行判断
            {
                ans[i] = flag1[i+1];
            }
            else
            {
                ans[i] = flag2[i+1];
            }
        }

        for( int i = 0; i < n; ++i )
        {
            cout << "Station " << ans[i] << " , " << i + 1 << std::endl;
        }
    }
#ifdef LOCAL
    cin.close();
    cout.close();
#endif
    return 0;
};

输入数据文件：input.dat
6
2 3
4 2
7 9 3 4 8 4
8 5 6 4 5 7
2 3 1 3 4
2 1 2 2 1
输出文件：output.dat
38
Station 1 , 1
Station 2 , 2
Station 1 , 3
Station 2 , 4
Station 2 , 5
Station 1 , 6