Description
给定一个长度为n的序列,从中选出一个子序列(不一定要连续,但是相对位置不能变化)。如1 2 3的子序列有{1,2,3} {1,2} {1,3} {2,3} {1,2,3}。{3,1}不是它的子序列。
要求这个子序列的元素是单调递增的。求出最长的满足条件的子序列。
LIS是经久不衰的dp入门题之一,本文通过对不同数据,不同复杂度的分析,来剖析LIS。
特别感谢小C大人的耐心讲解以及大犇shuangde800对
O(nlogn)
算法的分析。
不同的数据范围有不同的解法:
一、
n
<=1000,
1) 最简单的dfs
我们可以发现这其实是一个取还是不取的问题:如果可以取这个比它小的数,那就取它,增加当前取的个数。如果当前数为a,位于x,则[1,x-1]中所有小于a的数都会被取到一遍:
int ans=0;
void dfs(int x,int sum){//当前数为x,已取sum个
if(sum>ans)ans=sum;
for(int i=x-1;i>=1;i--)
if(a[i]<a[x])dfs(i,sum+1);
}上面这种方法显著的特点是从后往前枚举,而且整体思路和通常的dfs无异,可谓暴力递归;同时,这种方法无法转化成LIS的通常dp解法,因为缺少决策。这里的决策其实本质是一样的,但略有出入:在所有符合题意的数中,找到最大值。而上述代码并没有体现出这点。
//int dp[M];
int dfs(int x){
int mx=0;
// if(dp[x])return dp[x];
for(int i=x-1;i>=1;i--)
if(a[i]<a[x]){
int tmp=dfs(i);
if(tmp>mx)mx=tmp;//决策之处
}
return mx+1;
// return dp[x]=mx+1;
}这样就可以产生决策,并且转化成类似dp的形式;同样,此时为了避免重复子序列,就可以进行记忆化搜索,如注释中的内容。
标准的记忆化dp写法 O(n2) :
int dp[M],ans=0;
void Dp(){//以i结尾的序列,可以取到的最长序列长度
for(int i=1;i<=n;i++){
int mx=0;
for(int j=1;j<i;j++)
if(a[j]<a[i]&&dp[j]>mx)mx=dp[j];
dp[i]=mx+1;
ans=max(ans,dp[i]);
}//O(n^2)
}2) 变换一下思路
刚才定义的dp[i]的意义是“以i结尾的序列,可以取到的最长序列长度”,考虑到 ai 的范围也在1000以内,我们可以有这样一个dp[i]:
- 以权值 ai 结尾的序列,在 [1,i−1] 可以取到的最长序列长度。
这样就有下面这个dp:
void Dp(){//以i这个权值结尾的序列,可以取到的最长序列长度
for(int i=1;i<=n;i++){
int mx=0;
for(int j=0;j<a[i];j++)
if(dp[j>mx])mx=dp[j];
dp[a[i]]=mx+1;
ans=max(ans,mx+1);
}//O(n^2)
}这个dp中dp维护的是对应权值在[1,x]段中的最大子序列长度。
可以证明的是,若
ai=aj=x(i<j)
,则
dpi≤dpj
,所以
dp[a[i]]
可以直接等于
mx+1
。
3) 下标与内部数据的交换
前面两种dp都是维护[1,x]中的最长子序列长度,而决策的因素是x或者a[x]。如果将两者对调一下呢?我们就会得到新的算法 O(nlogn) :
- dp[len]→ 长度为 len 的最长子序列末尾的最小权值。
现在想想,我们用到了单调栈来实现 O(logn) 的转移复杂度。在单调栈中,序列长度是在依次增加的,而序列的末尾权值也是在依次变大的。对于 ai ,它能接在所有末位元素权值 ≤ai 的后面,而通过单调栈我们已经得到所有符合条件的可能序列长度,之后通过二分查找就可以找到最大满足序列。
#include<cstdio>
#include<algorithm>
#define M 1005
using namespace std;
int a[M],dp[M];
int main(){
int n,len=1;
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
dp[1]=a[1];
for(int i=2;i<=n;i++)
if(a[i]>dp[len])dp[++len]=a[i];//长度增加
else{
int p=lower_bound(dp+1,dp+1+len,a[i])-dp;
dp[p]=a[i];
}
printf("%d\n",len);
return 0;
}4) 采用树状数组的神奇解法(16/9/26更新)
此时树状数组不是维护前缀和,而是维护该段前缀内的最大值。我们就把权值作为下标,维护[1,x-1]的dp最大值即可。由于会出现0的情况,我们还要把每个数据都+1。也是数据结构优化 O(n)→O(logn) 。
#include <cstdio>
#include <cstring>
#define M 1005
#define lowbit(x) x&(-x)
int n,bit[M],a[M],ans=0;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);++a[i];
int x=a[i]-1,m=0;
while(x){
if(bit[x]>m)m=bit[x];
x-=lowbit(x);
}++m;
if(ans<m)ans=m;
x=a[i];
while(x<M){
if(m>bit[x])bit[x]=m;
x+=lowbit(x);
}
}printf("%d\n",ans);
}二、
n
<=
回到第二个Dp():
如果用“以i这个权值(即a[i])结尾的序列,可以取到的最长序列长度”去处理这个数据范围,有两个明显的困难与缺点:无法开到这么大的数组;数据过于分散,大量dp[]其实是被浪费的。
处理数据过于分散,我们需要在预处理中加入优化算法:离散化 O(nlogn) 。
int a[M],s[M];
int main(){
for(int i=0;i<n;i++){
scanf("%d",&a[i]);
s[i]=a[i];
}
sort(s,s+n);//使用的前提是数组已经有序
int m=unique(s,s+n)-s;
// for(int i=0;i<n;i++)if(s[m-1]!=s[i])s[m++]=s[i];//两种去重方法
for(int i=0;i<n;i++)a[i]=lower_bound(s,s+n)-s;
}//O(nlogn);运用离散化,相当于把a的范围重新缩小到 ai <= 103 :
这样lower_bound前后a数组的效果不变。
在第二个Dp()中的4、5行,发现这个操作只是在dp中寻找最大值,此时应该考虑用数据结构维护最大值的信息。我们可以采用线段树
O(nlogn)
做法:
#include<cstdio>
#include<algorithm>
using namespace std;
const int M=10005;
int a[M],s[M];
struct Segment{//叶子节点存储的是dp[a[i]],动态维护[1,x]的最大子序列长度
struct Node{
int L,R,mx;
int mid(){return (L+R)>>1;}
}tree[M<<2];
void down(){}
void up(int node){
tree[node].mx=max(tree[node<<1].mx,tree[node<<1|1].mx);
}
void build(int L,int R,int node){
tree[node].L=L;tree[node].R=R;tree[node].mx=0;
if(L==R){
scanf("%d",&a[L]);
s[L]=a[L];
return;
}
int mid=(L+R)>>1;
build(L,mid,node<<1);
build(mid+1,R,node<<1|1);
}
void updata(int x,int a,int node){
if(tree[node].L==tree[node].R){
tree[node].mx=max(tree[node].mx,a);
return;
}
int mid=tree[node].mid();
if(x<=mid)updata(x,a,node<<1);
else updata(x,a,node<<1|1);
up(node);
}
int query(int L,int R,int node){
if(L>R)return 0;
if(tree[node].L==L&&tree[node].R==R){
return tree[node].mx;
}
int mid=tree[node].mid();
if(R<=mid)return query(L,R,node<<1);
else if(L>mid)return query(L,R,node<<1|1);
else return max(query(L,mid,node<<1),query(mid+1,R,node<<1|1));
}
}Tree;//封装了完整的线段树全部操作
int Dp(int n){
int ans=0;
for(int i=1;i<=n;i++){
int k=Tree.query(1,a[i]-1,1);
Tree.updata(a[i],k+1,1);
ans=max(ans,k+1);
}
return ans;
}
int main(){
int n;
scanf("%d",&n);
Tree.build(1,n,1);
sort(s+1,s+n+1);
int m=unique(s+1,s+n+1)-(s+1);
for(int i=1;i<=n;i++)
a[i]=lower_bound(s+1,s+m,a[i])-s;
printf("%d\n",Dp(n));
return 0;
}






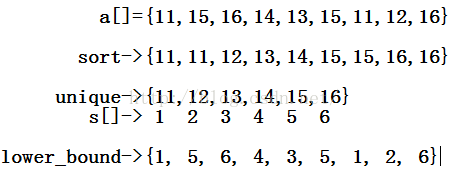














 450
450

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








