目录:
多变量线性回归(模型、梯度下降技巧)
特征选择和多项式回归
正规方程
- 代价函数:和单变量回归一样
多变量线性回归(模型、梯度下降技巧)
特征选择和多项式回归
正规方程
Matlab学习
1 多变量线性回归
1)模型- 假设函数:
- 代价函数:和单变量回归一样
- 梯度下降:
2)梯度下降算法的实用技巧
- 特征缩放(Feature Scaling)
均值归一化
u为该特征平均值;s为范围,也就是max-min
- 学习率 alpha
0.001,0.01,0.1……直到开始发散(alpha太小,收敛太慢;alpha太大可能会发散)
2 特征选择和多项式回归
特征是有很多选择的








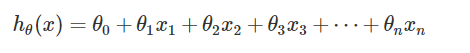
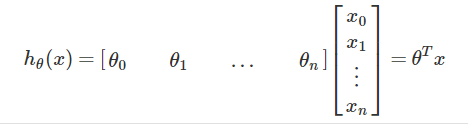
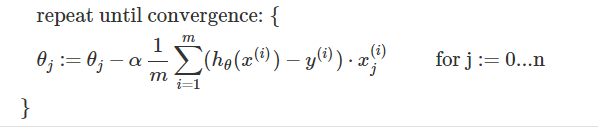
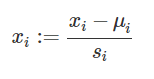
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 8万+
8万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








