CCFCSP201312-3最大的矩形

题目
http://118.190.20.162/view.page?gpid=T3

问题描述
　　在横轴上放了n个相邻的矩形，每个矩形的宽度是1，而第i（1 ≤ i ≤ n）个矩形的高度是hi。这n个矩形构成了一个直方图。例如，下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。

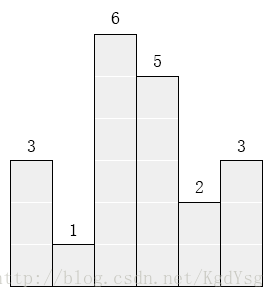
　　请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是10。

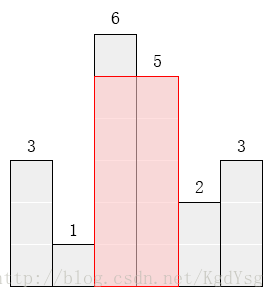
输入格式
　　第一行包含一个整数n，即矩形的数量(1 ≤ n ≤ 1000)。
　　第二行包含n 个整数h1, h2, … , hn，相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
输出格式
　　输出一行，包含一个整数，即给定直方图内的最大矩形的面积。
样例输入
6
3 1 6 5 2 3
样例输出
10

/*
http://118.190.20.162/view.page?gpid=T3
*/
#include <iostream>
using namespace std;
int main()
{
    int n;
    cin>>n;
    int num[n];
    for(int i = 0; i < n; i++)
    {
        cin>>num[i];
    }
    int ans = -1;
    for(int i = 0; i < n; i++)
    {
        int low = num[i];
        for(int j = i; j < n; j++)
        {
            if(low > num[j])
            {
                low = num[j];
            }
            int temp = (j - i + 1) * low;
            if(temp > ans)
            {
                ans = temp;
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

/*
    从第i个矩形开始向后遍历
    遍历到第j个矩形，找到从i到j中最小的值（高度） * (j-i+1)（宽度）
    如果这个面积比ans大就存入这个面积
    时间复杂度为O(n2) 
*/