1. 杂项
1.1 pi计算
pi = acos(-1);
1.2 减小误差
尽量少用三角函数、除法、开方、求幂、取对数运算
1.0 / 2.0 ∗ 3.0 / 4.0 ∗ 5.0 = ( 1.0 ∗ 3.0 ∗ 5.0 ) / ( 2.0 ∗ 4.0 )
a/b > c ---- a > bc
1.3 判等
(x-y)<eps
//取代 (x==y)
1.4 负零
小心不要输出-0,比如:
double a = -0.00001;
printf("%.4lf",a);
//解决 (sgn函数在下方)
double NoNegativeZero(double x){return !sgn(x)?fabs(x):x;}//防止输出-0
1.5 反三角函数
double x = 1.000001;
double acx = acos(x);
//可能会返回runtime error
//此时应加一句判断
double x = 1.000001;
if(fabs(x - 1.0) < eps || fabs(x + 1.0) < eps)
x = round(x);
double acx = acos(x);
1.6 舍入取整
double x = 1.49999;
int fx = floor(x);//向下取整函数
int cx = ceil(x);//向上取整函数
int rx = round(x);//四舍五入函数
printf("%f %d %d %d\n", x, fx, cx, rx);
//输出结果 1.499990 1 2 1
1.7 符号判断
const double eps = 1e-6;
int sgn(double x){return (x>eps)-(x<-eps);};
1.8 常用模板
#include <bits/stdc++.h>
#define ll long long
#define lf double
#define IOS std::ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define Rep(i, l, r) for (int i = (l); i <= (r); i++)
using namespace std;
struct Point {double x, y;};
typedef Point vector_t;
typedef Point point_t;
struct Line {Point x;vector_t v;};
double Cross(const vector_t& x, const vector_t& y) {
return x.x * y.y - x.y * y.x;
} //叉积
vector_t operator*(const vector_t& v, double t) {
return (vector_t){v.x * t, v.y * t};
}
vector_t operator+(const vector_t& a, const vector_t& b) {
return (vector_t){a.x + b.x, a.y + b.y};
}
Point operator-(const Point& a, const Point& b) {
return (Point){a.x - b.x, a.y - b.y};
}
const double eps = 1e-8;
bool cmp1(const Line& a, const Line& b) {
return atan2(a.v.y, a.v.x) < atan2(b.v.y, b.v.x);
} //极角排序
bool Onleft(Line l, Point p) { return Cross(l.v, (p - l.x)) > 0; } // ToLeftTest
int dcmp(double x) {
if (fabs(x) < eps) return 0;if (x > 0) return 1;return -1;
} //double的正负判断,sgn一样
int main() {double ans = 0; printf("%.2f", ans); }//用.f而不是.lf
2. 向量
以下均建立在左手系下。
typedef struct { float x, y, z, w; } vector_t;
typedef vector_t point_t;
2.1 点乘(内积)
double Dot(vector_t A, vector_t B){return A.x*B.x + A.y*B.y + A.z*B.z;}
2.2 叉乘(外积)
//左手系从x转向y
vector_t Cross(const vector_t& x, const vector_t& y)
{
vector_t z;
z.x = x.y * y.z - x.z * y.y;
z.y = x.z * y.x - x.x * y.z;
z.z = x.x * y.y - x.y * y.x;
z.w = 1.0f;//vector_t有{x,y,z,w},ACM可不管w
return z;
}
之后讨论Cross(a,b)==0和Cross(a,b)!=0时,均指对求出的向量的z值进行判断。
当讨论2维时,Cross的结果也指z值。
2.3 常用函数
//取模(长度)
double Length(vector_t A){return sqrt(Dot(A, A));}
//计算两向量夹角
double Angle(vector_t A, vector_t B){
return acos(Dot(A, B) / Length(A) / Length(B));
}
//计算向量逆时针旋转后的向量,2维
vector_t Rotate(vector_t A, double rad){//rad为弧度 且为逆时针旋转的角
return vector_t(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));
}
//计算向量逆时针旋转九十度的单位法向量,2维
vector_t Normal(vector_t A){//向量A左转90°的单位法向量
double L = Length(A);
return vector_t(-A.y/L, A.x/L);
}
//ToLeftTest
//判断向量ap是不是在向量ab的左边,是的话返回1 (不包括在ab上)
bool ToLeftTest(Point a, Point b, Point p){return sgn(Cross(b - a, p - a)) > 0;}
//极角排序
//将角度按逆时针排序
//方法1:atan2()函数,速度快精度低
int cmp(const Point&a,const Point&b){
Point aa=a-p[0],bb=b-p[0];//p[0]是原点的意思
double at1=atan2(aa.y,aa.x),at2=atan2(bb.y,bb.x);
if(at1-at2<eps) {return Length(aa)<=Length(bb);}
return at1<at2;
}
//方法2:叉乘,精度高速度慢
bool cmp2(point_t origin, point_t a, point_t b)
{
double f=Cross(a-origin,b-origin);
if(f==0) return Length(a-origin)<=Length(b-origin);
else if(f>0) return true;
return false;
}
//如果不是全在某一象限的点,需要先象限排序(?存疑)
int Quadrant(point_t a)//象限排序,注意包含四个坐标轴
{
if(a.x>0&&a.y>=0) return 1;
if(a.x<=0&&a.y>0) return 2;
if(a.x<0&&a.y<=0) return 3;
if(a.x>=0&&a.y<0) return 4;
}
bool cmp1(point a,point b)//先象限后极角
{
if(Quadrant(a)==Quadrant(b))//返回值就是象限
return cmp2(a,b);
else Quadrant(a)<Quadrant(b);
}
3. 点、线
3.1 定义结构体

struct Point{
double x,y;
};
typedef Point vector_t;
struct Line{
Point x;
vector_t v;
};
3.2 直线
3.2.1 判断点在直线上
利用三点共线时 a × b == 0
直线上取两不同点与待测点构成向量求叉积是否为零
3.2.2 计算两直线交点,2维
//调用前需保证 Cross(v, w) != 0
point_t GetLineIntersection(point_t P, vector_t v, point_t Q, vector_t w){
vector_t u = P-Q;
double t = Cross(w, u)/Cross(v, w);
return P+v*t;//由直线的点向式而来
}
推导(利用 交点到定点的向量×直线方向向量 = 0)
3.2.3 计算点到直线距离
//点P到直线AB距离公式
double DistanceToLine(point_t P, point_t A, point_t B){
Vector v1 = B-A, v2 = P-A;
return fabs(Cross(v1, v2)/Length(v1));
}//不去绝对值,得到的是有向距离
3.2.4 求点在直线上的投影点
//点P在直线AB上的投影点
Point GetLineProjection(point_t P, point_t A, point_t B){
vector_t v = B-A;
return A+v*(Dot(v, P-A)/Dot(v, v));
}
3.3 线段
3.3.1 判断点是否在线段上
bool OnSegment(Point p, Point a1, Point a2){
//注意有时Cross的判断会因为精度过高为错,看情况删除
// Dot==0,允许在端点
return (sgn(Cross(a1-p, a2-p)) == 0 && sgn(Dot(a1-p, a2-p)) <= 0);
}
3.3.2 点到线段距离
如果点与线段的垂足不在线段上,就是点与最近的端点的距离
double Dis_P_S(point_t p,point_t a,point_t b)
{
if(a==b)return Length(p-a);
vector_t v1 = b-a,v2 = p-a,v3 = p-b;
if(v1*v2<=0)return Length(v2);
else if(v1*v3>=0)return Length(v3);
else return Cross(v1,v2)/Length(v1);
}
3.3.3 求线段的过定点的垂足
Point P_L(Point p,Line l)
{
//*是点乘的意思
return l.p+l.v*(((p-l.x)*l.v)/(l.v*l.v));
}
3.3.4 判断两线段是否相交
使用跨立实验
跨立实验:

//不允许在顶点处相交
//线段a1a2,b1b2
bool SegmentProperIntersection(point_t a1, point_t a2, point_t b1, point_t b2){
double c1 = Cross(a2 - a1, b1 - a1), c2 = Cross(a2 - a1, b2 - a1);
double c3 = Cross(b2 - b1, a1 - b1), c4 = Cross(b2 - b1, a2 - b1);
return (sgn(c1)*sgn(c2) < 0 && sgn(c3)*sgn(c4) < 0);
//sgn():判断符号,返回-1,0,1
}
//允许在端点处相交
bool SegmentProperIntersection(point_t a1, point_t a2, point_t b1, point_t b2){
//这里的Cross是对二维处理,返回z值
double c1 = Cross(a2-a1, b1-a1), c2 = Cross(a2-a1, b2-a1);
double c3 = Cross(b2-b1, a1-b1), c4 = Cross(b2-b1, a2-b1);
//if判断控制是否允许线段在端点处相交,根据需要添加
if(!sgn(c1) || !sgn(c2) || !sgn(c3) || !sgn(c4)){
bool f1 = OnSegment(b1, a1, a2);
bool f2 = OnSegment(b2, a1, a2);
bool f3 = OnSegment(a1, b1, b2);
bool f4 = OnSegment(a2, b1, b2);
bool f = (f1|f2|f3|f4);
return f;
}
return (sgn(c1)*sgn(c2) < 0 && sgn(c3)*sgn(c4) < 0);
}
4. 三角形
4.1 三角形面积
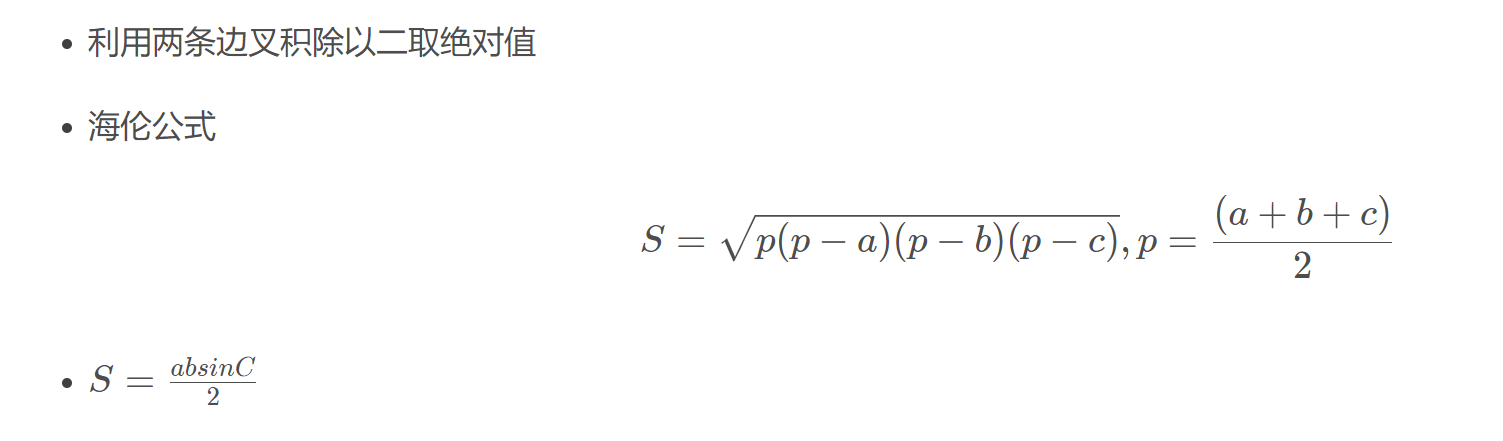
海伦公式误差比较大,一般用叉积。
4.2 三角形4心
外心: 三边中垂线交点,到三角形三个顶点距离相同。外心也是三角形外接圆的圆心。
内心: 角平分线的交点,到三角形三边的距离相同。
垂心: 三条高线的交点。
重心: 三条中线的交点,到三角形三顶点距离的平方和最小的点,三角形内到三边距离之积最大的点。
4.3 判断三角形类型
设三角形最长边为 c
显然,直角三角形是 a*a+b*b==c*c
锐角为 a*a+b*b>c*c
钝角为 a*a+b*b<c*c
4.4 求三角形外接圆
struct Circle{Point o;double r;};
Circle GetCircumcircleTriangle(const Point& p1, const Point& p2, const Point&p3)
{
double a,b,c,d,e,f;
a=p1.x-p2.x; b=p1.y-p2.y; c=(Dot(p2,p2)-Dot(p1,p1))/2;
d=p1.x-p3.x; e=p1.y-p3.y; f=(Dot(p3,p3)-Dot(p1,p1))/2;
double x=(f*b-c*e) / (a*e-b*d);
double y=(f*a-c*d) / (b*d-e*a);
Point o={x,y};double r=Length(p1-o);
return (Circle){o,r};
}
5.矩形
5.1 求矩形相交面积
//a[0]为矩形A左下角点,a[1]为矩形A右上角点,b[]同理
double RectIntersectS(Point a[2],Point b[2])
{
double maxx1 = max(a[0].x,a[1].x),minx1=min(a[0].x,a[1].x);
double maxy1 = max(a[0].y,a[1].y),miny1=min(a[0].y,a[1].y);
double maxx2 = max(b[0].x,b[1].x),minx2=min(b[0].x,b[1].x);
double maxy2 = max(b[0].y,b[1].y),miny2=min(b[0].y,b[1].y);
double ans = 0.0;
if(minx2 >= maxx1 || minx1 >= maxx2 || miny2 >= maxy1 || maxy2 <= miny1){
; //矩形不相交
}
else{
double xx = max(minx1,minx2), yy = max(miny1,miny2);
double x = min(maxx1,maxx2), y = min(maxy1,maxy2);
ans = abs(x-xx)*abs(y-yy);
}
return ans;
}
5.2 已知正方形对角点, 求另外两点
void CalSquarePoints(Point s[4]){ //已知点0,2; 求1,3.
double xc = (s[0].x + s[2].x) / 2.0, yc=(s[0].y + s[2].y)/ 2.0;
s[1].x = xc - (s[0].y - yc), s[1].y = yc - (xc - s[0].x);
s[3].x = xc + (s[0].y - yc), s[3].y = yc + (xc - s[0].x);
}
6. 多边形、散点
6.1 凸多边形
定义: 过多边形的一条边做一条直线,如果其他各个顶点都在这条直线的同侧,若所有边均成立,则把这个多边形叫做凸多边形。
任意凸多边形外角和均为360°
任意凸多边形内角和为(n - 2) · 180°
6.2 多边形面积
6.2.1求多边形面积
可以选一个顶点固定,把凸多边形分成n−2个三角形,然后把面积加起来
double PolygonArea(point_t* p, int n){//p为端点集合,n为端点个数
double s = 0;
for(int i = 1; i < n-1; ++i)
s += Cross(p[i]-p[0], p[i+1]-p[0]);
return abs(s/2);
}
6.2.2 求2个多边形(凹凸)面积交/并
double GetCPIArea(Point a[], Point b[], int na, int nb)
//ConvexPolygonIntersectArea
{
Point p[505], tmp[505];//大小应该>=max(na,nb)
int i, j, tn, sflag, eflag;
a[na] = a[0], b[nb] = b[0];
memcpy(p, b, sizeof(Point) * (nb + 1));//注意n大小,防止超时
for(i = 0; i < na && nb > 2; ++ i)
{
sflag = dcmp(Cross(a[i+1]-a[i], p[0]-a[i]));
for(j = tn = 0; j < nb; ++ j, sflag = eflag)
{
if(sflag >= 0) tmp[tn ++] = p[j];
eflag = dcmp(Cross(a[i+1]-a[i], p[j+1]-a[i]));
if((sflag ^ eflag) == -2)
tmp[tn ++] = GetLineIntersection(a[i], a[i+1]-a[i], p[j], p[j+1]-p[j]);
}
memcpy(p, tmp, sizeof(Point) * tn);
nb = tn, p[nb] = p[0];
}
if(nb < 3) return 0.0;
return PolygonArea(p, nb);
}
double GetSPIArea(Point a[], Point b[], int na, int nb)
{
//多边形面积并=两个多边形面积和-面积交
int i, j;
Point t1[4], t2[4];
double res = 0, if_clock_t1, if_clock_t2;
a[na] = t1[0] = a[0], b[nb] = t2[0] = b[0];
for(i = 2; i < na; ++ i)
{
t1[1] = a[i - 1], t1[2] = a[i];
if_clock_t1 = dcmp(Cross(t1[1]-t1[0], t1[2]-t1[0]));
if(if_clock_t1 < 0) std::swap(t1[1], t1[2]);
for(j = 2; j < nb; ++ j)
{
t2[1] = b[j - 1], t2[2] = b[j];
if_clock_t2 = dcmp(Cross(t2[1]-t2[0], t2[2]-t2[0]));
if(if_clock_t2 < 0) std::swap(t2[1], t2[2]);
//res为相交部分的面积
res += GetCPIArea(t1, t2, 3, 3) * if_clock_t1 * if_clock_t2;
}
}
return PolygonArea(a, na) + PolygonArea(b, nb) - res;
}
6.3 判断点是否在多边形内(任意多边形)
//判断点是否在多边形内,若点在多边形内返回1,在多边形外部返回0,在多边形上返回-1
int isPointInPolygon(point_t p, vector<point_t> poly){
int wn = 0;
int n = poly.size();
for(int i = 0; i < n; ++i){
if(OnSegment(p, poly[i], poly[(i+1)%n])) return -1;
int k = sgn(Cross(poly[(i+1)%n] - poly[i], p - poly[i]));
int d1 = sgn(poly[i].y - p.y);
int d2 = sgn(poly[(i+1)%n].y - p.y);
if(k > 0 && d1 <= 0 && d2 > 0) wn++;
if(k < 0 && d2 <= 0 && d1 > 0) wn--;
}
if(wn != 0)
return 1;
return 0;
}
6.4 判断点是否在凸多边形内
只需要判断点是否在所有边的左边(按逆时针顺序排列的顶点集)ToLeftTest
6.5 皮克定理
皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式该公式可以表示为:
2S = 2a + b - 2
其中a表示多边形内部的点数,b表示多边形顶点数,S表示多边形的面积。
常用:给你多边形的顶点,问多边形内部有多少点
a = S - b/2 + 1
6.6 散点建凸包
大体做法是,将点排序,先按x升序再按y升序(或者极角排序?)。
然后按逆时针顺序建凸包。要保证的是,凸包上先后两条边的叉积是恒为正的,相当于一条向量逆时针转了一圈。
建完第一遍之后,我们得到的是下凸包,这时候再反着扫一遍,依然保证叉积恒为正即可。
Point p[500];
bool operator <(Point a,Point b){
return (abs(a.y-b.y)<eps)?a.x<b.x:a.y<b.y;
}//先y升序再x升序
int build(int n,Point *p,Point *s)
{
//*p为散点,*s为凸包的点,p[]从0开始
//注意判断所有点是否在一条直线,该算法会把所有点在一条直线的情况归为凸包
sort(p,p+n);//这里是重载了小于符号的
int m = 0;
for(int i = 0;i < n;i++)
{
while(m>1&&Cross((s[m-1]-s[m-2]),(p[i]-s[m-2]))<=0)m--;
s[m++] = p[i];
}
int lim = m;
for(int i = n-2;i >= 0;i--)
{
while(m>lim&&Cross((s[m-1]-s[m-2]),(p[i]-s[m-2]))<=0)m--;
s[m++] = p[i];
}
if(m!=1)m--;
//注意范围 s[0,m)
return m;
}
6.7 直线切割凸包(返回直线左边的点)
暴力扫,用叉积判断点是否在直线左边(或直线上)。如果直线与凸包某一线段相交就把交点扔进去。
typedef vector<Point> Pol;
Pol Cut_Pol(Pol p,Line l)
{
Pol ret;int n = p.size();
for(int i=0;i<n;i++)
{
Point p0 = p[i],p1 = p[(i+1)%n];
if(dcmp(l.v^(p0-l.x))>=0)ret.push_back(p0);
if(dcmp(l.v^(p1-p0)))
{
Point tmp = L_L(l,Line(p0,p1-p0));//L_L():求两条直线相交交点
if(P_S(tmp,p0,p1))ret.push_back(tmp);
//P_S():判断点是否在线段上
}
}
return ret;
}
6.8 求凸包直径
凸包直径就是凸包上两个不相邻点的距离的最大值。
用旋转卡壳的思路做:
想象有一对平行的夹子,一段夹在凸包的某条边上,另一端自己转,两个夹子对应凸包4个点,然后可以从4个点中找出直径。
double Pol_d(Pol p)
{
int n = p.size();
int i = 0,j = 1;p[n]=p[0];
double ans = 0.0;
for(;i<n;i++)
{
while(j<n&&
Cross((p[j+1]-p[i+1]),(p[i]-p[i+1]))>Cross((p[j]-p[i+1]),(p[i]-p[i+1])))
{j=(j+1)%n;}
ans = max(ans, max(Length(p[j]-p[i]),Length(p[j+1]-p[i+1])));
}
return ans;
}
6.9 求半平面交
参考
简单理解就是多边形的所有边相交后剩下的块,看下图应该很容易理解,蓝色部分就是半平面交:
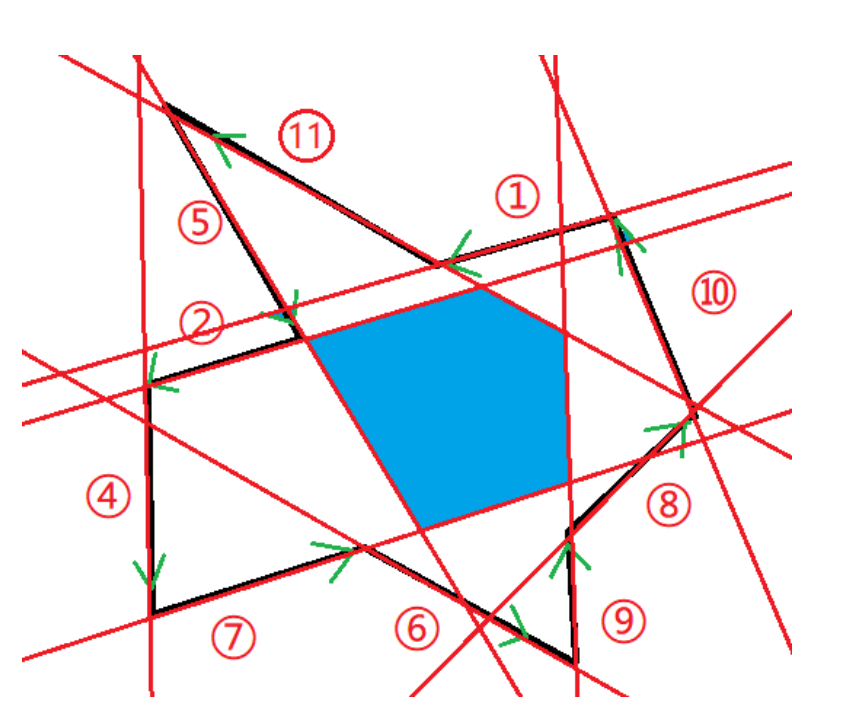
用处有:
求最大内切圆;
求多边形的核(求解一个区域,可以看到给定图形的各个角落);
Point tmpP[500];
Line tmpL[500];
bool cmp1(const Line& a,const Line& b) {
return atan2(a.v.y,a.v.x)<atan2(b.v.y,b.v.x);
}//极角排序
int dcmp(double x){ if(fabs(x)<eps)return 0; if(x>0)return 1; return -1;}
bool Onleft(Line l,Point p) { return dcmp(Cross(l.v,(p-l.x))) > 0; }//ToLeftTest
int HalfPol(Line *l,int n,vector<Point> &p)
{
sort(l,l+n,cmp1);//把边按极角排序
int hd = 0,tl = 0;
tmpL[0] = l[0];
for(int i=0;i<n;i++)
{
while(hd<tl&&!Onleft(l[i],tmpP[tl-1]))tl--;
while(hd<tl&&!Onleft(l[i],tmpP[hd]))hd++;
tmpL[++tl] = l[i];
if(!dcmp(Cross(tmpL[tl].v,tmpL[tl-1].v)))
{
tl--;
if(Onleft(tmpL[tl],l[i].x))tmpL[tl]=l[i];
}
if(hd<tl)tmpP[tl-1] = GetLineIntersection(tmpL[tl-1],tmpL[tl]);//求两直线交点,不写在这里了
}
while(hd<tl&&!Onleft(tmpL[hd],tmpP[tl-1]))tl--;
if(tl-hd<=1)return 0;
tmpP[tl] = GetLineIntersection(tmpL[hd],tmpL[tl]);
for(int i=hd;i<=tl;i++)p.push_back(tmpP[i]);
return tl-hd+1;
}
6.10 求散点的费马点(费马点到所有给定点的距离之和最短)
费马点:给n个散点,求平面一点到所有给定点的距离之和最短。所求点叫做费马点。
用贪心模拟退火的方法可以求出费马点。(因为费马点就在散点中心附近,所以可以贪心)
Point GetFermatPoint(const Point* p, int n) //p[0,n)
{
double offset[4][2]={{1,0}, {-1,0}, {0,1}, {0,-1}};//往4个方向走
double step=100,lx=1e18,rx=-1e18,ly=1e18,ry=-1e18;
for(int i=0;i<n;i++){
lx=min(lx,p[i].x); ly=min(ly,p[i].y);
rx=max(rx,p[i].x); ry=max(ry,p[i].y);
}
step=max(step,max(rx-lx,ry-ly));//求出步长,步长其实越大越好,因为每次除以2,收敛很快
Point s=p[0];
double ans=1e18;
while(step>eps){//注意eps应该小于题目要求的精度
int jug=0;
for(int i=0;i<4;i++){
Point d={s.x+offset[i][0],s.y+offset[i][1]};
double tot=0;
for(int j=0;j<n;j++){tot += Length(d-p[j]);}
if(tot<ans){s=d; ans=tot; jug=1;}//如果能走,就走过去
}
if(jug==0){step/=2.0;}//如果不能走,说明步长太大
}
return s;
}
7. 圆
只需要知道圆心和半径即可,可以知道圆上任一角度点的坐标
struct Circle
{
Point p;
double r;
Point point(double rad){return Point(p.x+r*cos(rad),p.y+r*sin(rad));}
};
7.1 点与圆、多边形与圆
7.1.1 过定点求圆切线
三种情况:
1.点在圆内,此时无切线;
2.点在圆上,此时切线与两点连线垂直;
3.点在圆外:

可直接求得θ,然后直线就好求了。
int T_P_C(Circle c,Point p,vector<Vector>&ve)
{
Vector v = c.p-p;
double dis = Length(v);
if(!dcmp(dis-c.r))
{
ve.push_back(Vector(-v.y,v.x));
return 1;
}else if(dcmp(dis-c.r)<0)return 0;
double rad = asin(c.r/dis);
ve.push_back(rot(v,rad));
ve.push_back(rot(v,-rad));
//rot(v,rad) : 直线v逆时针转动rad后的直线
return 2;
}
7.1.2 求多边形(凹凸)与圆相交面积
point_t GetLineIntersection(point_t P, vector_t v, point_t Q, vector_t w){
vector_t u = P-Q;
double t = Cross(w, u)/Cross(v, w);
return P+v*t;//由直线的点向式而来
}
double LineCrossCircle(const Point &a, const Point &b, Circle c,
Point &p1, Point &p2)//p1,p2为交点
{
Point fp = GetLineIntersection(c.o, Point(a.y - b.y, b.x - a.x), a, b-a);
double rtol = Length(c.o-fp);
double rtos = OnSegment(fp,a,b) ? rtol : min(Length(a-c.o), Length(b-c.o));
double atob = Length(b-a);
double fptoe = sqrt(c.r * c.r - rtol * rtol) / atob;
if(rtos > c.r - eps) return rtos;
p1 = fp + (a - b) * fptoe;
p2 = fp + (b - a) * fptoe;
return rtos;
}
double SectorArea(const Point &o, const Point &a, const Point &b, double R)
//不大于180度扇形面积,o->a->b逆时针
{
double A2 = Dot(o-a, o-a), B2 = Dot(o-b, o-b), C2 = Dot(a-b, a-b);
return R * R * acos((A2 + B2 - C2) * 0.5 / sqrt(A2) / sqrt(B2)) * 0.5;
}
double GetTriCirIntersect(const Point &o, const Point &a, const Point &b, double R)
//Get Triangle and Circle Intersect,逆时针,o为圆心
{
double adis = Length(a-o), bdis = Length(b-o);
if(adis < R + eps && bdis < R + eps) return Cross(a-o, b-o) * 0.5;
Point ta, tb;
if(sgn(Cross(a-o, b-o))==0) return 0.0;
double rtos = LineCrossCircle(a, b, Circle(o,R), ta, tb);
if(rtos > R - eps) return SectorArea(o, a, b, R);
if(adis < R + eps)
return Cross(a-o, tb-o) * 0.5 + SectorArea(o, tb, b, R);
if(bdis < R + eps)
return Cross(ta-o, b-o) * 0.5 + SectorArea(o, a, ta, R);
return Cross(ta-o, tb-o) * 0.5 +
SectorArea(o, a, ta, R) + SectorArea(o, tb, b, R);
}
double GetPolCirIntersect(const Point* p, int n, Circle c)
//Get Polygon and Circle Intersect
{
//只验证了圆心在(0,0)处,应该圆心变化也是正确的
double ans=0;
Rep(i,0,n-1){
int isClock = sgn(Cross(p[i]-c.o,p[(i+1)%n]-c.o));
if(isClock<0)ans-=GetTriCirIntersect(c.o,p[(i+1)%n],p[i],c.r);
else ans+=GetTriCirIntersect(c.o,p[i],p[(i+1)%n],c.r);
}
return abs(ans);
}
7.2 直线与圆
7.2.1 直线与圆交点
显然三种情况:
圆心到直线距离>半径,此时没有交点;
圆心到直线距离=半径,此时交点为垂足;
圆心到直线距离<半径,此时交点有两个:
有两个交点时,我们已知斜边=半径,一条直角边=圆心到直线距离,那么另一条直角边边长可求,搞出高线法向量即可求出两个点坐标。
//Line有一个点和一个方向向量
int L_C(Line l, Circle c, vector<Point>&ve)
{
Point p = c.p;double r = c.r,dis = Dis_P_L(p,l);
if(dcmp(dis-r)>0)return 0;
//dcmp():double的大小比较
else if(!dcmp(dis-r))
{
ve.push_back(P_L(p,l));
//P_L():求点在直线的投影
return 1;
}
Point h = P_L(p,l);Vector tmp = Nol(h-p);
//Nol():求二维直线的平面法向量
double len = sqrt(r*r-dis*dis);
ve.push_back(h+tmp*len);
ve.push_back(h-tmp*len);
//点的加减就是x,y对应加减
return 2;
}
7.3 圆与圆
7.3.1 圆与圆交点
分几种情况:
圆心重合,若半径相同则无数条,半径不同则无交点;
圆心不重合,若相离则无交点;

最后就是相交有1或2个交点,可以发现三角形三边都已知,那么暴力余弦定理可求得夹角,再根据角度计算圆上一点。
int C_C(Circle a, Circle b, vector<Point>&ve)
{
double dis = Length(a.p-b.p);
if(!dcmp(dis))
{
if(!dcmp(a.r-b.r))return -1;
return 0;
}
if(dcmp(a.r+b.r-dis)<0)return 0;
double rad = ang(b.p-a.p);
//ang():计算向量和x轴(也是个向量)夹角
double dlt = acos((a.r*a.r+dis*dis-b.r*b.r)/(2*a.r*dis));
Point p1 = a.point(rad+dlt),p2 = a.point(rad-dlt);
if(p1==p2)
{
ve.push_back(p1);
return 1;
}else
{
ve.push_back(p1);
ve.push_back(p2);
return 2;
}
}
7.3.2 圆与圆公切线
情况很多,可从内切开始慢慢推导:


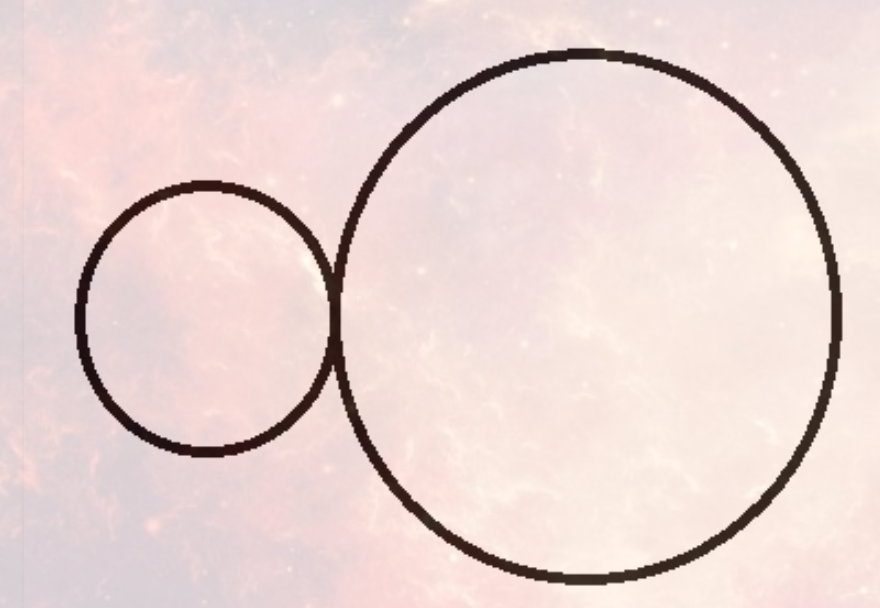
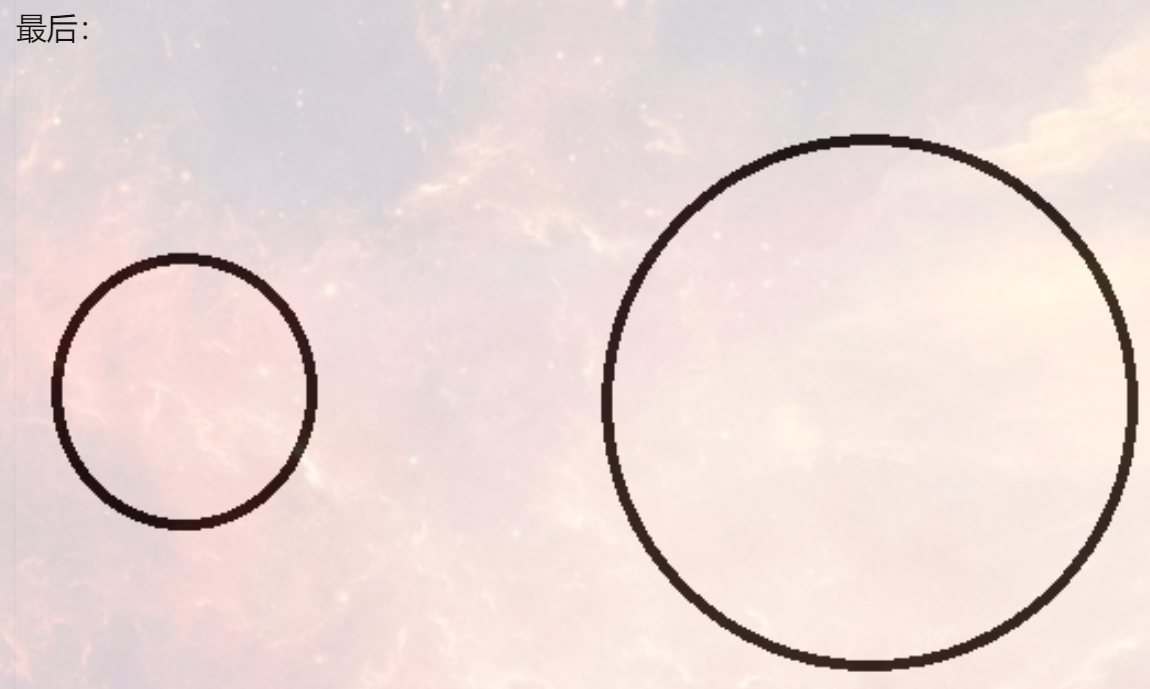
讲解:https://www.cnblogs.com/LiGuanlin1124/p/10963724.html
int T_C_C(Circle a,Circle b,vector<Point>&pa,vector<Point>&pb)
{
if(a.r>b.r)swap(a,b),swap(pa,pb);
double dis = lth(a.p-b.p),rd = fabs(a.r-b.r),rs = a.r+b.r;
if(dcmp(dis-rd)<0)return 0;
if(!dcmp(dis)&&!dcmp(a.r-b.r))return -1;
double rad = ang(b.p-a.p);//向量和x轴夹角
if(!dcmp(dis-rd))
{
pa.push_back(a.point(rad)),pb.push_back(b.point(rad));
//a.point(rad):已知rad求圆上一点
return 1;
}
double drad = acos(rd/dis);
pa.push_back(a.point(rad+drad)),pb.push_back(b.point(rad+drad));
pa.push_back(a.point(rad-drad)),pb.push_back(b.point(rad-drad));
if(!dcmp(dis-rs))
{
pa.push_back(a.point(rad)),pb.push_back(b.point(-rad));
return 3;
}else if(dcmp(dis-rs)>0)
{
drad = acos(rs/dis);
pa.push_back(a.point(rad+drad)),pb.push_back(b.point(rad-drad));
pa.push_back(a.point(rad-drad)),pb.push_back(b.point(rad+drad));
return 4;
}else return 2;
}
8 球体
8.1 球与球
8.1.1 求两球体积交/并
const ld pi=acos(-1);
ld pow2(ld x){return x*x;}
ld pow3(ld x){return x*x*x;}
ld dis(ld x1,ld y1,ld z1,ld x2,ld y2,ld z2){
return pow2(x1-x2)+pow2(y1-y2)+pow2(z1-z2);
}
ld cos(ld a,ld b,ld c){return (b*b+c*c-a*a)/(2*b*c);}
ld cap(ld r,ld h){return pi*(r*3-h)*h*h/3;}
//2球体积交
ld sphere_intersect(ld x1,ld y1,ld z1,ld r1,ld x2,ld y2,ld z2,ld r2)
{
ld d=dis(x1,y1,z1,x2,y2,z2);
//相离
if(d>=pow2(r1+r2))return 0;
//包含
if(d<=pow2(r1-r2))return pow3(min(r1,r2))*4*pi/3;
//相交
ld h1=r1-r1*cos(r2,r1,sqrt(d)),h2=r2-r2*cos(r1,r2,sqrt(d));
return cap(r1,h1)+cap(r2,h2);
}
//2球体积并
ld sphere_union(ld x1,ld y1,ld z1,ld r1,ld x2,ld y2,ld z2,ld r2)
{
ld d=dis(x1,y1,z1,x2,y2,z2);
//相离
if(d>=pow2(r1+r2))return (pow3(r1)+pow3(r2))*4*pi/3;
//包含
if(d<=pow2(r1-r2))return pow3(max(r1,r2))*4*pi/3;
//相交
ld h1=r1+r1*cos(r2,r1,sqrt(d)),h2=r2+r2*cos(r1,r2,sqrt(d));
return cap(r1,h1)+cap(r2,h2);
}
8.2 球与点
8.2.1 从经纬度获取球上一点坐标、获取球上两点绕球的最短距离
double radians(double angle){return angle*PI/180;}
struct Sphere{
Point3 o={0,0,0};double r;
Point3 GetCoord(double latitude, double longitude){//纬度以北为正,经度以东为正
latitude=radians(latitude);
longitude=radians(longitude);
Point3 p;
p.x=r*cos(latitude)*cos(longitude);
p.y=r*cos(latitude)*sin(longitude);
p.z=r*sin(latitude);
p=p+o;
return p;
}
double GetDisAB(Point3 a, Point3 b){
double d=Length3(a-b);
double rad=2*asin(d/2/r);
return rad*r;
}
};
























 1058
1058











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








