吴恩达 深度学习 编程作业（1-3）- Planar data classification with one hidden layer

---

吴恩达Coursera课程 DeepLearning.ai 编程作业系列，本文为《神经网络与深度学习》部分的第三周“浅层神经网络”的课程作业（做了无用部分的删减）。

另外，本节课程笔记在此：《吴恩达Coursera深度学习课程 DeepLearning.ai 提炼笔记（1-3）》，如有任何建议和问题，欢迎留言。

---

Planar data classification with one hidden layer

1 - Packages

Let’s first import all the packages that you will need during this assignment.
- numpy is the fundamental package for scientific computing with Python.
- sklearn provides simple and efficient tools for data mining and data analysis.
- matplotlib is a library for plotting graphs in Python.
- testCases_v2 provides some test examples to assess the correctness of your functions
- planar_utils provide various useful functions used in this assignment

# Package imports
import numpy as np
import matplotlib.pyplot as plt
from testCases_v2 import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

%matplotlib inline

np.random.seed(1) # set a seed so that the results are consistent

You can get the support code from here.

2 - Dataset

First, let’s get the dataset you will work on. The following code will load a “flower” 2-class dataset into variables X and Y.

def load_planar_dataset():
    np.random.seed(1)
    m = 400 # 样本数量
    N = int(m/2) # 每个类别的样本量
    D = 2 # 维度数
    X = np.zeros((m,D)) # 初始化X
    Y = np.zeros((m,1), dtype='uint8') # 初始化Y
    a = 4 # 花儿的最大长度

    for j in range(2):
        ix = range(N*j,N*(j+1))
        t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
        r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
        X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
        Y[ix] = j

    X = X.T
    Y = Y.T

    return X, Y


X, Y = load_planar_dataset()

Visualize the dataset using matplotlib. The data looks like a “flower” with some red (label y=0) and some blue (y=1) points. Your goal is to build a model to fit this data.

# Visualize the data:
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);

You have:
- a numpy-array (matrix) X that contains your features (x1, x2)
- a numpy-array (vector) Y that contains your labels (red:0, blue:1).

Lets first get a better sense of what our data is like.

Exercise: How many training examples do you have? In addition, what is the shape of the variables X and Y?

Hint: How do you get the shape of a numpy array? (help)

### START CODE HERE ### (≈ 3 lines of code)
shape_X = X.shape
shape_Y = Y.shape
m = X.shape[1]  # training set size
### END CODE HERE ###

print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
print ('I have m = %d training examples!' % (m))

The shape of X is: (2, 400)
The shape of Y is: (1, 400)
I have m = 400 training examples!

3 - Simple Logistic Regression

Before building a full neural network, lets first see how logistic regression performs on this problem. You can use sklearn’s built-in functions to do that. Run the code below to train a logistic regression classifier on the dataset.

# Train the logistic regression classifier
clf = sklearn.linear_model.LogisticRegressionCV();
clf.fit(X.T, Y.T);

You can now plot the decision boundary of these models. Run the code below.

# Plot the decision boundary for logistic regression
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
plt.title("Logistic Regression")

# Print accuracy
LR_predictions = clf.predict(X.T)
print ('Accuracy of logistic regression: %d ' % float((np.dot(Y,LR_predictions) + np.dot(1-Y,1-LR_predictions))/float(Y.size)*100) +
       '% ' + "(percentage of correctly labelled datapoints)")

Accuracy of logistic regression: 47 % (percentage of correctly labelled datapoints)

plot_decision_boundary:

def plot_decision_boundary(model, X, y):
    # Set min and max values and give it some padding
    x_min, x_max = X[0, :].min() - 1, X[0, :].max() + 1
    y_min, y_max = X[1, :].min() - 1, X[1, :].max() + 1
    h = 0.01
    # Generate a grid of points with distance h between them
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    # Predict the function value for the whole grid
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # Plot the contour and training examples
    plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
    plt.ylabel('x2')
    plt.xlabel('x1')
    plt.scatter(X[0, :], X[1, :], c=y, cmap=plt.cm.Spectral)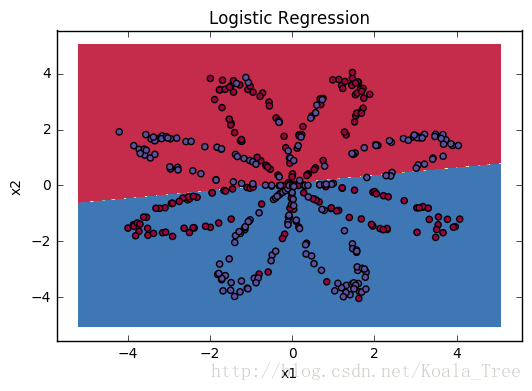

Interpretation: The dataset is not linearly separable, so logistic regression doesn’t perform well. Hopefully a neural network will do better. Let’s try this now!

4 - Neural Network model

Logistic regression did not work well on the “flower dataset”. You are going to train a Neural Network with a single hidden layer.

Here is our model:

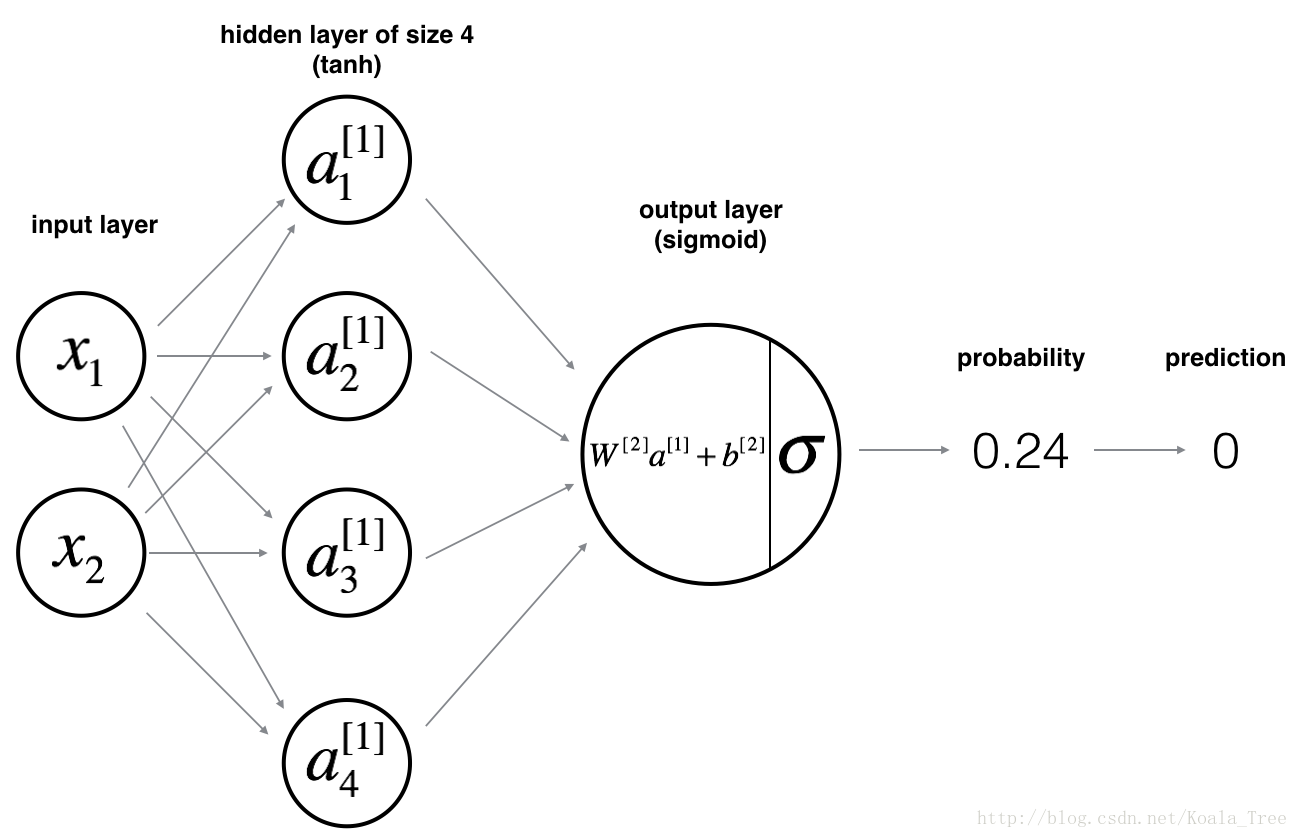
Mathematically:

For one example $x^{(i)}$:

$$z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\tag{1}$$
$$a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2}$$

z[2](i)=W[2]a[<