线性分类器设计

线性分类器设计

本节内容：本节内容是根据上学期所上的模式识别课程的作业整理而来，第二道题目是线性分类器设计，数据集是Iris(鸢尾花的数据集)。

---

判别函数

• 分类的基本原理
  不同模式对应特征点在特征空间里散布，运用已知类别的样本进行学习和训练，产生若干个代数界面，即判别边界，这些判别边界将特征空间划分成一些互不交叠的的子区域。

• 判别函数
  表示界面的函数，就是判别函数。假设对一模式X已抽取n个特征，表示为：$X=(x_1,x_2,x_3,\ldots,x_n)^T,X$是n维空间的一个向量。模式识别问题就是根据模式X的n个特征来判别模式属于ω1 ,ω2 , … , ωm类中的哪一类。
  

• 线性可分的定义
  如果不同的模式在特征空间的里的分布相互分离，且它们之间存在有一个线性的判别边界，那么表示边界的函数也叫做线性判别函数，此时，称这些模式是线性可分的，线性判别函数是统计模式识别的基本方法之一，简单且容易实现。

  ---

线性判别函数

我们现在对两类问题和多类问题分别进行讨论

• 两类问题：$\omega_i=(\omega_1,\omega_2)^T,M=2$

  • 二维情况
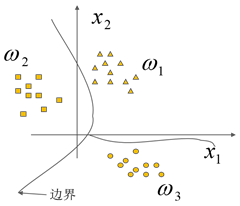
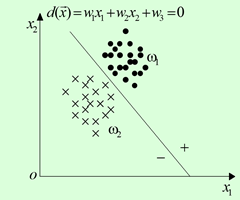
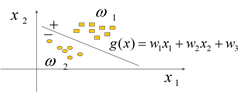
    $X=(x_1,x_2)^T,n=2$,这种情况下，判别函数：$g(x)=\omega_1x_1+\omega_2x_2+\omega_3,\omega为参数，x_1,x_2为向量坐标$。
    在两类别情况，判别函数 g (x) 具有以下性质：
    

    $$g_i(x)=\left\{ \begin{array}{rcl} >0 & & {X\in\omega_1}\\ =0 & &{X不定}\\ <0 & & {X\in\omega_2}\\ \end{array} \right.$$
    这是二维情况下判别由判别边界分类。情况如图：
    

  • n维问题
    现抽取n个特征为：$X=(x_1,x_2,x_3,\ldots,x_n)^T$,判别函数为：
    

    $$\begin{eqnarray*} g(x) & =&\omega_1x_1+&\omega_2x_2+&\cdots +&\omega_nx_n+&\omega_{n+1} \\ & = &W_0+&\omega_{n+1} \end{eqnarray*}$$
    $W_0=(\omega_0,\omega_1,\ldots,\omega_n)^T$为权向量，$X=(x_1,x_2,\ldots,x_n)$为模式向量。
    另一种增广表示法：$g(x)=W^TX$,$W=(\omega_0,\omega_1,\ldots,\omega_n,\omega_{n+1})^T$为增广权向量，$X=(x_1,x_2,\ldots,x_n,x_{n+1})$为增广模式向量。
    模式分类：
    $$g(x)=W^TX=\left\{ \begin{array}{rcl} >0 & & {x\in\omega_1}\\ =0 & &{x不定}\\ <0 & & {x\in\omega_2}\\ \end{array} \right.$$
    当 $g_1(x) =W^TX=0$ 为判别边界。
    当n=2时，二维情况的判别边界为一直线。
    当n=3时，判别边界为一平面。
    当n>3时，则判别边界为一超平面。

• 多类问题：模式有 ω1 ,ω2 , … , ωm 个类别，可分三种情况：

  • 第一种情况：每一模式类与其它模式类间可用单个判别平面把一个类分开。这种情况，M类可有M个判别函数，且具有以下性质：
    

    $$g_i(x)=W_i^TX\left\{ \begin{array}{rcl} >0 & & {X\in\omega_1}\\ <0 & & {其他，i=1,2,\cdots,M}\\ \end{array} \right.$$
    式中$W_i=(\omega_{i1},\omega_{i2},\ldots,\omega_{in},\omega_{in+1})^T$为第i个判别函数的权向量。
    此种情况可以理解为$\omega_i/\overline{\omega_i}$二分法。

  • 第二种情况：每个模式类和其它模式类间可分别用判别平面分开，一个判别界面只能分开两个类别，不一定能把其余所有的类别分开；这种情况可理解为$\omega_i/\omega_j$二分法，这样有M(M-1)/2个判别平面。对于两类问题，M=2，则有一个判别平面。同理，三类问题则有三个判别平面。
    判别函数：$g_{ij}(x)=W_{ij}^TX$
    判别边界：$g_{ij}(x)=0$
    判别条件：

    $$g_{ij}(x)=\left\{ \begin{array}{rcl} >0 & & {x\in\omega_i}\\ <0 & & {x\in\omega_j}\\ \end{array} \right. 其中i\not=j$$
    判别函数性质：$g_{ij}(x)=-g_{ji}(x)$
    结论：判别区间增大，不确定区间减小，比第一种情况小的多。

  • 第三种情况：每类都有一个判别函数,存在M个判别函数，这种情况可理解为无不确定区的$\omega_i/\omega_j$二分法。
    判别函数：$g_{K}(x)=W_{K}^TX,K=1,2,\cdots,M$
    判别边界：$g_{i}(x)=g_j(x)$
    判别条件：

    $$g_{i}(x)=W_{K}^TX\left\{ \begin{array}{rcl} 最大 & & {x\in\omega_i}\\ 小 & & {其他}\\ \end{array} \right.$$
    就是说，要判别模式X属于那一类，先把X代入M个判别函数中，判别函数最大的那个类别就是X所属类别。类与类之间的边界可由$g_i(x) =g_j(x)$ 或$g_i(x) -g_j(x) =0$来确定。

• 关于线性判别函数的结论
  模式类别若可用任一线性判别函数来划分，这些模式就称为线性可分；一旦线性判别函数的参数确定，这些函数即可作为模式分类的基础。
  对于M（M≥2）类模式分类，第一、三种情况需要M个判别函数，第二种情况需要M(M-1)/2个判别函数。
  对于第一种情况，每个判别函数都要把一种类别（比如i类）的模式与其余M-1种类别的模式划分开，而不是仅将一类与另一类划分开。
  实际上，一个类的模式分布要比M-1类模式分布更聚集，因此后两种情况实现模式线性可分的可能性要更大一些。

---

线性分类器设计

• 设计线性分类器的主要步骤
  收集一组具有类别标识的样本$\{X_1,X_2,\cdots,X_n\}$ 。若把每个样本看成确定的观测值，则这组样本称为确定性样本集；若把每个样本看成随机变量，则这组样本称为随机样本集。
  根据实际情况确定一个准则函数J。J必须满足：
  a) J是样本集X和W 、w_n+1 的函数；
  b) J的值反映分类器的性能，其极值解对应于“最好”的决策。
  用最优化技术求出准则函数的极值解$W^*,\omega_{n+1}^*$，

• 结论
  训练过程就是对已知类别的样本集求解权向量Ｗ，这是一个线性联立不等式方程组求解的过程。
  求解时：
  只有对线性可分的问题，$g(x) =W^TX$才有解
  联立方程的解是非单值，在不同条件下，有不同的解，所以就产生了求最优解的问题
  求解W的过程就是训练的过程。训练方法的共同点是，先给出准则函数，再寻找使准则函数趋于极值的优化算法，不同的算法有不同的准则函数。同时，算法可以分为迭代法和非迭代法。

感知器法（迭代法）

基本思路：通过对W的调整，可实现判别函数：
$g(x) =W^TX > R_T 其中RT为响应阈值$
定义感知准则函数准则：只考虑错分样本
定义：$J(W)=\sum_{X\in X_0}(-W^TX) ,其中X_0为错分样本$
当分类发生错误时就有$W^TX <0，或－W^TX >0$, 所以J(W) 总是正值，错误分类愈少，J(W)就愈小。理想情况为$J(W)=0$，即求最小值的问题.
感知器算法

1.错误分类修正w_k
如$w_k^Tx≤0并且x∈ω_1 ,w_{k+1}= w_k+ρ_kx$
如$w_k^Tx≥0并且x∈ω_2 , w_{k+1}= w_k-ρ_kx$
2.正确分类 ，w_k不修正
如$w_k^Tx＞0并且x∈ω_1$
如$w_k^Tx＜0并且x∈ω_2$
3.赏罚概念
感知器算法显然是一种赏罚过程。对正确分类的模式则“赏”（此处用“不罚”，即权向量W不变）；对错误分类的模式则“罚”，使W加上一个正比于错误模式样本X的分量。
4.$\rho_k$的选取法则
- 固定增量原则：ρk固定非负数
- 绝对修正规则：$\rho_k>\frac{\left| \omega^Tx \right |}{x^Tx}$
- 部分修正规则：$\rho_k>\lambda\frac{\left| \omega^Tx \right |}{x^Tx},0<\lambda\leq2$

最小平方误差准则（非迭代法）

定义误差向量：$e=XW-b≠0$ 把平方误差作为目标函数
$J(W)=\left \| e \right \|^2=\left \| XW-b \right \|^2=\sum_{i=1}^N(W^TX_i-b_i)$
W的优化就是使J(W)最小。于是，求J(W)的梯度并令其为0，即
$\nabla J(W)=\sum_{i=1}^N2(W^TX_i-b_i)X_i=2X^T(XW-b)=0$
解上方程得 $X^TXW=X^Tb$,这样把求解XW=b的问题，转化为对 $X^TXW=X^Tb$求解，这样最大好处是：因$X^TX$是方阵且通常是非奇异的，所以可以得到W的唯一解。此时，最小平方误差法同Fisher法是一致

Fisher分类准则

设计线性分类器：$g(x)=\omega^Tx+\omega_0$,首先要确定准则函数；然后再利用训练样本集确定该分类器的参数，以求使所确定的准则达到最佳。
在使用线性分类器时，样本的分类由其判别函数值决定，而每个样本的判别函数值是其各分量的线性加权和再加上一阈值w0。
Fisher准则的基本原理，就是要找到一个最合适的投影轴，使两类样本在该轴上投影的交迭部分最少，从而使分类效果为最佳。
维数映射：$Y=W^TX+W_0$,即完成从X空间到Y空间的映射。
在X空间的均值：

$$\overline x_i=\frac {1}{N_i}\sum_{x \in X_i}x,i=1,2$$
在Y空间的投影均值：
$$\overline y_i=\frac {1}{N_i}\sum_{y \in Y_i}y=\frac {1}{N_i}\sum_{x \in X_i}W^Tx=W^T\overline x_i,i=1,2$$
$\therefore \overline Y_1=W^T\overline X_1,\overline Y_2=W^T\overline X_2$
投影样本之间的分离性用投影样本之差表示: $\left| \overline Y_1- \overline Y_2 \right|=\left| W^T(\overline X_1- \overline X_2 )\right|$类间分离性越大越好。
投影样本类内离散度:
$\sigma_i^2=\sum_{y \in Y_i}(y- \overline y_i)^2=W^TS_iW$
其中 $S_i=\sum_{x \in X_i}(x-\overline x_i)(x-\overline x_i)^T,\sigma_1^2=W^TS_1W,\sigma_1^2=W^TS_2W$
投影样本总的离散度为: $\sigma_1^2+\sigma_2^2$,则总的离散度越小越好。故 Fisher准则函数有： $$J(W)=\frac {\left| \overline Y_1- \overline Y_2 \right|^2}{(\sigma_1^2+\sigma_2^2)}$$
进一步化简，可以得到：

$$J(W)=\frac {W^TS_bW}{W^TS_wW},其中S_b类内散布矩阵，S_w是类间散布矩阵$$
$S_b=(\overline x_1-\overline x_2)(\overline x_1-\overline x_2)^T,S_w=S_1+S_2,对J(W)求极值， 可以得到W=S_w^{-1}(\overline x_1-\overline x_2)$

上式称为广义Rayleigh商，其极值可用Lagrange乘子法求解。其极值解是n维x空间向一维y空间的最好投影方向，它实际是多维空间向一维空间的一种映射。

现在我们已把一个n维的问题转化为一维的问题。在该一维空间设计 Fisher分类器:

$$Y=W^TX>W_0\Rightarrow X \in \omega_1 \\ Y=W^TX<W_0\Rightarrow X \in \omega_2$$
因此，此时只要确定一个合适的阈值W ₀，将投影点y与W0比较即可进行分类决策。
W₀的选择

• $W_0=\frac {\overline y_1 +\overline y_2}{2}$
• $W_0=\frac {N_1\overline y_1 +N_2\overline y_2}{N_1+N_2}=\frac {N_1W^T\overline x_1 +N_2W^T\overline x_2}{N_1+N_2}$
• $W_0=\overline y_1 +(\overline y_2-\overline y_1)\frac {\sum_{k=1}^{N_1}(y_{k1}-\overline y_1)^2}{\sum_{k=1}^{N_1}(y_{k1}-\overline y_1)^2+\sum_{k=1}^{N_2}(y_{k2}-\overline y_2)^2}$,y_ki表示第i类中第k个样本的投影值,N1为ω1样本数，N2为ω2样本数 ,当W0选定后，对任一样本X，只要判断$Y=W^TX>W_0$ 则X∈ω1;$Y=W^TX<W_0$，则X∈ω2。于是，分类问题就解决了。