算法思想篇（4）————分治算法

在编程过程中，我们经常遇到处理数据相当多、求解过程比较复杂、直接求解法会比较耗时的问题。在求解这类问题时，我们可以采用“各个击破”的方法。具体做法是先把这个问题分解成几个较小的子问题，找到求出这几个子问题的解法后，再找到合适的方法，把它们组合成求整个大问题的解法。如果这些子问题还是比较大，还可以继续再把它们分成几个更小的小子问题，以此类推，直至可以直接求出解为止。这就是分治策略的基本思想。
使用分治算法解题的一般步骤如下所示。
（1）分解，将要解决的问题划分成若干个规模较小的同类问题；
（2）求解，当子问题划分得足够小时，用较简单的方法解决；
（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解
下面通过一个例子来说明分治算法的思想：
假设有n队队伍参加球赛，初赛阶段采用循环制，比赛共进行n-1天。每队要和其他各队进行一场比赛，然后按照积分选拔进入决赛的球队，要求每队每天只能参加一场比赛，并且不能轮空，按上述需求安排比赛日程。
代码如下：

//start from the very beginning,and to create greatness
//@author: Chuangwei Lin
//@E-mail：979951191@qq.com
//@brief： 比赛安排
#include <stdio.h>
#define MAXN 64 //定义最大球队数量
int a[MAXN+1][MAXN+1]={0};//存放比赛日程数组
/******************************************************
函数名：gamecal(int k,int n)
参数：编号k，球队数量n
功能：处理编号k开始的n个球队的日程 
*******************************************************/
void gamecal(int k,int n)
{
    int i,j;
    if(n==2)//若只有2队
    {
        a[k][1]=k;  //参赛球队编号
        a[k][2]=k+1; //对阵球队编号
        a[k+1][1]=k+1; //参赛球队编号 
        a[k+1][2]=k; //对阵球队编号 
    }
    else
    {
        //队伍减半处理，这部分就是分治算法的思想
        gamecal(k,n/2);//先处理前一半
        gamecal(k+n/2,n/2);//处理后一半
        //利用对称关系填充日程表
        for(i=k;i<k+n/2;i++) //填充右上角 
        {
            for(j=n/2+1;j<=n;j++)
            {
                a[i][j]=a[i+n/2][j-n/2];
            }
        }
        for(i=k+n/2;i<k+n;i++) //填充右下角 
        {
            for(j=n/2+1;j<=n;j++)
            {
                a[i][j]=a[i-n/2][j-n/2];
            }
        }
    }
}

int main()
{
    int m,i,j;
    printf("参赛球队数：");
    scanf("%d",&m);
    j=2;
    for(i=2;i<8;i++)//这判断是不是2的整数幂
    {
        j=j*2;
        if(j==m) break;
    }
    if(i>=8)//大于2的6次方就出错
    {
        printf("参赛球队数必须为2的整数次幂，并且不超过64！\n");
        return 0; 
    }
    gamecal(1,m);//处理第一队
    printf("\n编号 ");//输出结果
    for(i=2;i<=m;i++)
        printf("%2d天 ",i-1);
    printf("\n");
    for(i=1;i<=m;i++)
    {
       for(j=1;j<=m;j++)
           printf("%4d ",a[i][j]);
       printf("\n");
    }
    return 0;    
}

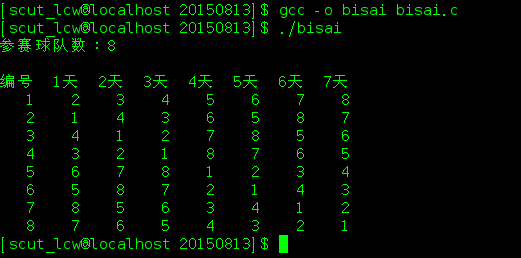
运行结果：