均值不等式

[题目]
已知六棱锥 $P-ABCDEF$ ，底面 $ABCDEF$ 为正六边形，点 $P$ 在底面的射影为其中心，将该六棱锥沿六条侧棱剪开，使六个侧面和底面展开在同一平面上，若展开后点 $P$ 在该平面上对应的六个点全部落在一个半径为 $5$ 的圆上，则当正六边形 $ABCDEF$ 的边长变化时，所得六棱锥体积的最大值为 $\underline{}$.

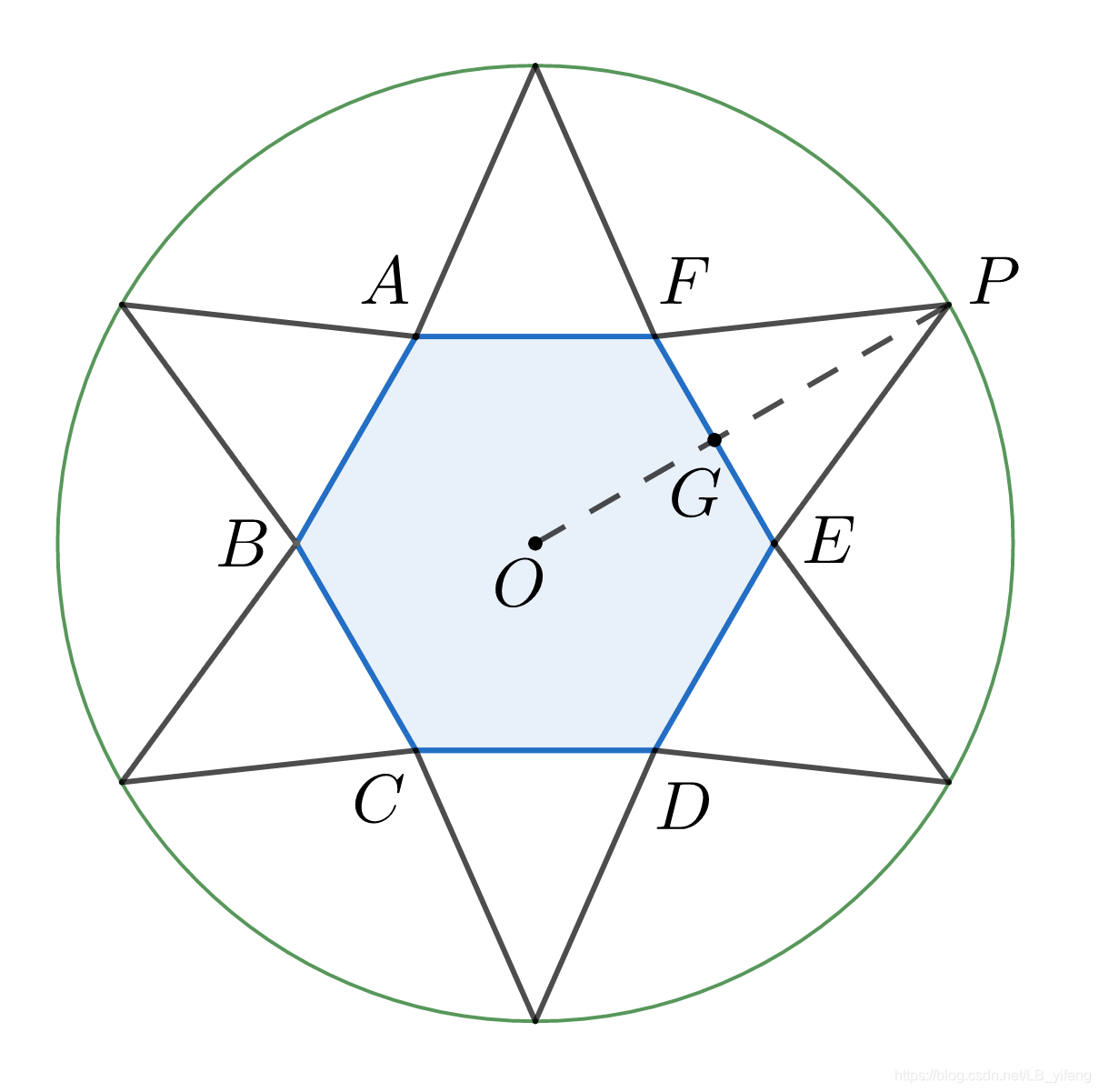
[解析]
如图，连接 $OP$ ，交 $EF$ 于 $G$ ，设 $OG=x$ ，则 $GP=5-x$ ，六棱锥的高 $h=\sqrt{25-10x},S_{ABCDEF}=2\sqrt{3}{x}^2$ . 则$$\begin{array}{rl}V& =\frac{1}{3}\cdot 2\sqrt{3}{x}^2\cdot \sqrt{25-10x}\\ & =\frac{2\sqrt{3}}{3}\cdot \frac{4}{25}\cdot \sqrt{(25-10x)\cdot \frac{5}{2}x\cdot \frac{5}{2}x\cdot \frac{5}{2}x\cdot \frac{5}{2}x}\\ & \le \frac{2\sqrt{3}}{3}\cdot \frac{4}{25}\cdot \sqrt{5^5}\\ & =\frac{8\sqrt{15}}{3}\end{array}$$当且仅当 $25-10x=\frac{5}{2}x$ ，即 $x=2$ 时，等号成立，六棱锥体积取最大值 $\frac{8\sqrt{15}}{3}$，此时六边形的边长为 $\frac{4\sqrt{3}}{3}$ .