CNN卷积神经网络原理详解(下)
反向传播
前面讲解了卷积神经网络的网络基本架构。我们在实际运算的时候会发现,随着计算次数的增加,我们的输出结果与我们的预期结果会不断的逼近。这是因为网络中的权重参数在不断的调整,那么参数是如何调整的?这就涉及到一个反向传播的问题。反向传播其实是神经网络的一个基础,下面我通过一个简单的示例带大家详细了解一下这个数学过程。
前向传播过程
了解反向传播之前,我们先来简单回顾一下前向传播的过程。也就是神经网络正常走完一个周期的过程。

如图所示,这是典型的神经网络的基本构成。其中L1层是输入层,L2层是隐藏层,L3层是输出层。假定我们现在输入一系列数组,我们希望最后的输出是我们预期的值,那么这些数组必然要经历一个参数的计算过程,下面我们通过一个具体的示例讲述一下这个变化是如何发生的。
首先我们明确初始条件
输入数据:
x
1
=
0.05
x_{1}=0.05
x1=0.05,
x
2
=
0.1
x_{2}=0.1
x2=0.1;
输出数据:
y
1
=
0.01
y_{1}=0.01
y1=0.01,
y
2
=
0.99
y_{2}=0.99
y2=0.99;
初始权重(随着计算的进行,权重会不断的更新迭代):
w
1
=
0.15
,
w
2
=
0.2
,
w
3
=
0.25
,
w
4
=
0.3
,
w
5
=
0.4
,
w
6
=
0.45
,
w
7
=
0.5
,
w
8
=
0.55
w_{1}=0.15,w_{2}=0.2,w_{3}=0.25, w_{4}=0.3,w_{5}=0.4,w_{6}=0.45,w_{7}=0.5,w_{8}=0.55
w1=0.15,w2=0.2,w3=0.25,w4=0.3,w5=0.4,w6=0.45,w7=0.5,w8=0.55;
偏置:
b
1
=
0.35
,
b
2
=
0.6
b_{1}=0.35,b_{2}=0.6
b1=0.35,b2=0.6.
激活函数为sigmoid函数(用激活函数是为了去线性化,具体原因我会在下次笔记中介绍)
这个神经网络的目的就是,我们给出一组输入,最后使得输出尽可能的接近 y 1 = 0.01 , y 2 = 0.99 y_{1}=0.01,y_{2}=0.99 y1=0.01,y2=0.99.
现在开始前向传播
(1)从L1层到L2层(输入层到隐藏层):
计算神经元
x
1
x_{1}
x1的输入加权和:
n
e
t
a
11
=
w
1
∗
x
1
+
w
2
∗
x
2
+
b
1
∗
1
net_{a11}=w_{1}*x_{1}+w_{2}*x_{2}+b_{1}*1
neta11=w1∗x1+w2∗x2+b1∗1
带入数据:
n
e
t
a
11
=
0.15
∗
0.05
+
0.2
∗
0.1
+
0.35
∗
1
=
0.3775
net_{a11}=0.15*0.05+0.2*0.1+0.35*1=0.3775
neta11=0.15∗0.05+0.2∗0.1+0.35∗1=0.3775
神经元
a
11
a_{11}
a11的输出为(对神经元执行一次sigmoid激活):
o
u
t
a
11
=
1
1
+
e
−
n
e
t
a
11
=
1
1
+
e
−
0.3775
=
0.593269992
out_{a11}=\frac{1}{1+e^{-net_{a11}}}=\frac{1}{1+e^{-0.3775}}=0.593269992
outa11=1+e−neta111=1+e−0.37751=0.593269992
同理可得
a
12
a_{12}
a12的输出为:
o
u
t
a
12
=
0.596884378
out_{a12}=0.596884378
outa12=0.596884378
(2)从L2层到L3层(隐藏层到输出层):
(此时的L2层相当于我们的输入层,计算过程类似上一层)
计算输出神经元
y
1
y_{1}
y1的输入加权和:
n
e
t
y
1
=
w
5
∗
o
u
t
a
11
+
w
6
∗
o
u
t
a
12
+
b
2
∗
1
net_{y1}=w_{5}*out_{a11}+w_{6}*out_{a12}+b_{2}*1
nety1=w5∗outa11+w6∗outa12+b2∗1
带入数据:
n
e
t
y
1
=
0.4
∗
0.593269992
+
0.45
∗
0.596884378
+
0.6
∗
1
=
1.105905967
net_{y1}=0.4*0.593269992+0.45*0.596884378+0.6*1=1.105905967
nety1=0.4∗0.593269992+0.45∗0.596884378+0.6∗1=1.105905967
o
u
t
y
1
=
1
1
+
e
−
n
e
t
y
1
=
1
1
+
e
−
1.105905967
=
0.75136507
out_{y1}=\frac{1}{1+e^{-net_{y1}}}=\frac{1}{1+e^{-1.105905967}}=0.75136507
outy1=1+e−nety11=1+e−1.1059059671=0.75136507
同理可得
y
2
y_{2}
y2的输出为:
o
u
t
y
2
=
0.772928465
out_{y2}= 0.772928465
outy2=0.772928465
这样前向传播的过程就结束了,我们得到的输出值为[0.75136507 , 0.772928465],与实际值[0.01 , 0.99]相差还很远,为了得到一组接近我们需要的数据,我们需要调整参数(神经网络的权重),重新计算输出。那么如何调整参数?我们应该知道当前参数对误差的总影响,具体的方法就是要进行反向传播计算。
反向传播过程
在进行反向传播之前,我们最后再回顾一下我们刚刚做了什么事情。
刚刚,我们首先定义了一组输入数值
X
X
X;
2,我们对输入数组执行第一册计算并将结果给到了隐藏层L2,我们假定这个函数为
F
(
x
)
F(x)
F(x);
3,我们对隐藏层进行了非线性处理,假定这一步操作为
S
(
F
(
x
)
)
S(F(x))
S(F(x));
4,接着我们将L2层视为新的输入层,对他执行了一系列变化并将值给到输出层L3,假定这一步操作为
G
(
S
(
F
(
x
)
)
)
G(S(F(x)))
G(S(F(x)));
5,最后我们对输出层执行了非线性变化,得到第一次计算的最终结果,这一步操作可以看做
T
(
G
(
S
(
F
(
x
)
)
)
)
T(G(S(F(x))))
T(G(S(F(x)))).
6,根据链式法则,现在我们要做的就是给这个多嵌套的函数脱衣服。。。
脱衣服的过程一定要遵循先穿的后脱,后穿的先脱(会不会被河蟹)。。。
开始脱衣服 反向传播:
1,计算总误差:
E t o t a l = ∑ 1 2 ( t a r g e t − o u t p u t ) 2 E_{total}=\sum \frac{1}{2}(target-output)^{2} Etotal=∑21(target−output)2
因为有两个输出,所以分我们别计算 y 1 y1 y1和 y 2 y2 y2的误差,然后计算两者之和:
E y 1 = 1 2 ( t a r g e t y 1 − o u t p u t y 1 ) 2 = 1 2 ( 0.01 − 0.75136507 ) 2 = 0.274811083 E_{y1}=\frac{1}{2}(target_{y1}-output_{y1})^{2}=\frac{1}{2}(0.01-0.75136507)^{2}=0.274811083 Ey1=21(targety1−outputy1)2=21(0.01−0.75136507)2=0.274811083
E y 2 0.023560026 E_{y2}0.023560026 Ey20.023560026
E t o t a l = E y 1 + E y 2 = 0.298371109 E_{total}=E_{y1}+E_{y2}=0.298371109 Etotal=Ey1+Ey2=0.298371109
输出层向隐藏层的权值更新:
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)
∂ E t o t a l ∂ w 5 = ∂ E t o t a l ∂ o u t y 1 ∗ ∂ o u t y 1 ∂ n e t y 1 ∗ ∂ n e t y 1 ∂ w 5 \frac{\partial E_{total}}{\partial w_{5}}=\frac{\partial E_{total}}{\partial out_{y1}}*\frac{\partial out_{y1}}{\partial net_{y1}}*\frac{\partial net_{y1}}{\partial w_{5}} ∂w5∂Etotal=∂outy1∂Etotal∗∂nety1∂outy1∗∂w5∂nety1
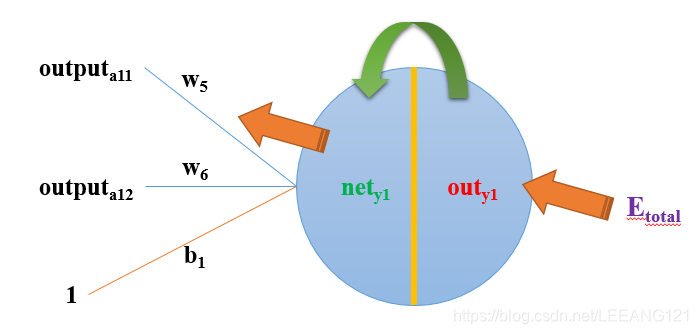
我们来计算每一个单独的算式:
计算 ∂ E t o t a l ∂ o u t y 1 \frac{\partial E_{total}}{\partial out_{y1}} ∂outy1∂Etotal
E t o t a l = 1 2 ( t a r g e t y 1 − o u t y 1 ) 2 + 1 2 ( t a r g e t y 2 − o u t y 2 ) 2 E_{total}=\frac{1}{2}(target_{y1}-out_{y1})^{2}+\frac{1}{2}(target_{y2}-out_{y2})^{2} Etotal=21(targety1−outy1)2+21(targety2−outy2)2
∂ E t o t a l ∂ o u t y 1 = 2 ∗ 1 2 ( t a r g e t y 1 − o u t y 1 ) 2 − 1 ∗ ( − 1 ) + 0 = − ( t a r g e t y 1 − o u t y 1 ) = − ( 0.01 − 0.75136507 ) = 0.74136507 \frac{\partial E_{total}}{\partial out_{y1}}=2*\frac{1}{2}(target_{y1}-out_{y1})^{2-1}*(-1)+0=-(target_{y1}-out_{y1})=-(0.01-0.75136507)=0.74136507 ∂outy1∂Etotal=2∗21(targety1−outy1)2−1∗(−1)+0=−(targety1−outy1)=−(0.01−0.75136507)=0.74136507
计算 ∂ o u t y 1 ∂ n e t y 1 \frac{\partial out_{y1}}{\partial net_{y1}} ∂nety1∂outy1
o u t y 1 = 1 1 + e − n e t y 1 out_{y1}=\frac{1}{1+e^{-net_{y1}}} outy1=1+e−nety11
∂ o u t y 1 ∂ n e t y 1 = o u t y 1 ( 1 − o u t y 1 ) \frac{\partial out_{y1}}{\partial net_{y1}}=out_{y1}(1-out_{y1}) ∂nety1∂outy1=outy1(1−outy1)
∂
o
u
t
y
1
∂
n
e
t
y
1
=
o
u
t
y
1
(
1
−
o
u
t
y
1
)
=
0.75136507
∗
(
1
−
0.75136507
)
=
0.186815602
\frac{\partial out_{y1}}{\partial net_{y1}}=out_{y1}(1-out_{y1})=0.75136507*(1-0.75136507)=0.186815602
∂nety1∂outy1=outy1(1−outy1)=0.75136507∗(1−0.75136507)=0.186815602
(这一步实际上就是对sigmoid函数求导)
计算
∂
n
e
t
y
1
∂
w
5
\frac{\partial net_{y1}}{\partial w_{5}}
∂w5∂nety1
n
e
t
y
1
=
w
5
∗
o
u
t
a
11
+
w
6
∗
o
u
t
a
12
+
b
2
∗
1
net_{y1}=w_{5}*out_{a11}+w_{6}*out_{a12}+b_{2}*1
nety1=w5∗outa11+w6∗outa12+b2∗1
带入数据得到
∂
n
e
t
y
1
∂
w
5
=
o
u
t
a
11
=
0.593269992
\frac{\partial net_{y1}}{\partial w_{5}}=out_{a11}=0.593269992
∂w5∂nety1=outa11=0.593269992
最后根据上面公式三者相乘:
∂
E
t
o
t
a
l
∂
w
5
=
0.74136507
∗
0.186815602
∗
0.593269992
=
0.082167041
\frac{\partial E_{total}}{\partial w_{5}}=0.74136507*0.186815602*0.593269992=0.082167041
∂w5∂Etotal=0.74136507∗0.186815602∗0.593269992=0.082167041
这样我们就求出了整体误差对
w
5
w_{5}
w5的偏导值。
我们再梳理一遍上面的计算公式:
∂ E t o t a l ∂ w 5 = − ( t a r g e t y 1 − o u t y 1 ) ∗ o u t y 1 ( 1 − o u t y 1 ) ∗ o u t a 11 \frac{\partial E_{total}}{\partial w_{5}}=-(target_{y1}-out_{y1})*out_{y1}(1-out_{y1})*out_{a11} ∂w5∂Etotal=−(targety1−outy1)∗outy1(1−outy1)∗outa11
现在我们来更新
w
5
w_{5}
w5的值:
w
5
+
=
w
5
−
η
∗
∂
E
t
o
t
a
l
∂
w
5
w_{5}^{+}=w_{5}-\eta *\frac{\partial E_{total}}{\partial w_{5}}
w5+=w5−η∗∂w5∂Etotal
其中:
1,
w
5
+
w_{5}^{+}
w5+是更新权重
2,
η
\eta
η是学习率
同理可以更新
w
6
,
w
7
,
w
8
w_{6},w_{7},w_{8}
w6,w7,w8的值如下:
w
6
=
0.408666186
w_{6}=0.408666186
w6=0.408666186
w
7
=
0.511301270
w_{7}=0.511301270
w7=0.511301270
w
8
=
0.561370121
w_{8}=0.561370121
w8=0.561370121
隐藏层向输入层的权值更新
计算方法与上面一样,但是需要注意一点。从L3层到L2层计算权重 w 5 w_{5} w5时,是从 o u t y 1 out_{y1} outy1到 n e t y 1 net_{y1} nety1再到 w 5 w_{5} w5;而从L2层到L1层就算权重 w 1 w_{1} w1(以 w 1 w_{1} w1为例),是从 o u t a 11 out_{a11} outa11到 n e t a 11 net_{a11} neta11再到 w 1 w_{1} w1,其中 o u t a 11 out_{a11} outa11,其中 o u t a 11 out_{a11} outa11接受的是从 E y 1 E_{y1} Ey1和 E y 2 E_{y2} Ey2两个方向传递的影响。
∂ E t o t a l ∂ w 1 = ∂ E t o t a l ∂ o u t a 11 ∗ ∂ o u t a 11 ∂ n e t a 11 ∗ ∂ n e t a 11 ∂ w 1 \frac{\partial E_{total}}{\partial w_{1}}=\frac{\partial E_{total}}{\partial out_{a11}}*\frac{\partial out_{a11}}{\partial net_{a11}}*\frac{\partial net_{a11}}{\partial w_{1}} ∂w1∂Etotal=∂outa11∂Etotal∗∂neta11∂outa11∗∂w1∂neta11
其中:
∂ E t o t a l ∂ o u t a 11 = ∂ E y 1 ∂ o u t a 11 + ∂ E y 2 ∂ o u t a 11 \frac{\partial E_{total}}{\partial out_{a11}}=\frac{\partial E_{y1}}{\partial out_{a11}}+\frac{\partial E_{y2}}{\partial out_{a11}} ∂outa11∂Etotal=∂outa11∂Ey1+∂outa11∂Ey2
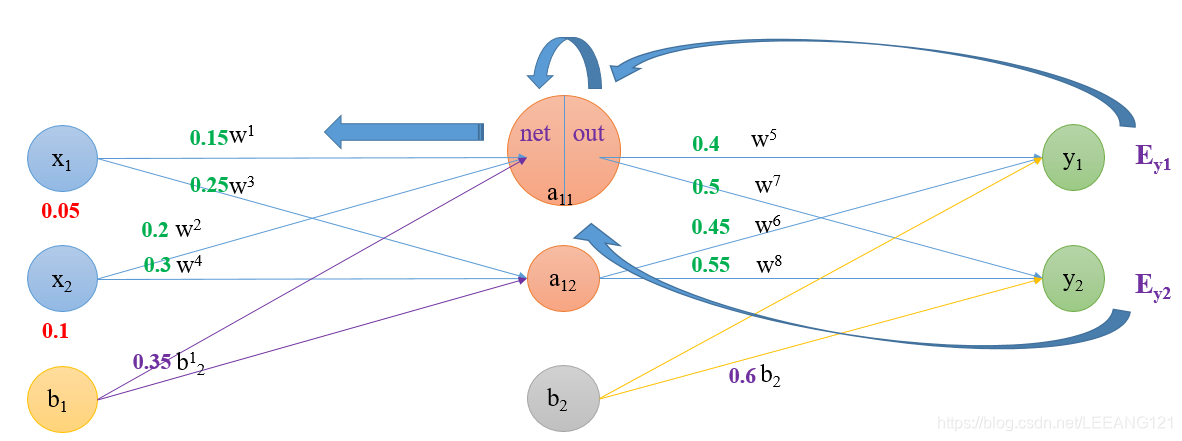
计算
∂
E
y
1
∂
o
u
t
a
11
\frac{\partial E_{y1}}{\partial out_{a11}}
∂outa11∂Ey1:
∂ E y 1 ∂ o u t a 11 = ∂ E y 1 ∂ n e t y 1 ∗ ∂ n e t y 1 ∂ o u t a 11 \frac{\partial E_{y1}}{\partial out_{a11}}=\frac{\partial E_{y1}}{\partial net_{y1}}*\frac{\partial net_{y1}}{\partial out_{a11}} ∂outa11∂Ey1=∂nety1∂Ey1∗∂outa11∂nety1
带入相关数据:
∂ E y 1 ∂ n e t y 1 = ∂ E y 1 ∂ o u t y 1 ∗ ∂ o u t y 1 ∂ n e t a 11 = 0.74136507 ∗ 0.186815602 = 0.138498562 \frac{\partial E_{y1}}{\partial net_{y1}}=\frac{\partial E_{y1}}{\partial out_{y1}}*\frac{\partial out_{y1}}{\partial net_{a11}}=0.74136507*0.186815602=0.138498562 ∂nety1∂Ey1=∂outy1∂Ey1∗∂neta11∂outy1=0.74136507∗0.186815602=0.138498562
n e t y 1 = w 5 ∗ o u t a 11 + w 6 ∗ o u t a 12 + b 2 ∗ 1 net_{y1}=w_{5}*out_{a11}+w_{6}*out_{a12}+b_{2}*1 nety1=w5∗outa11+w6∗outa12+b2∗1
∂ n e t y 1 ∂ o u t a 11 = w 5 = 0.40 \frac{\partial net_{y1}}{\partial out_{a11}}=w_{5}=0.40 ∂outa11∂nety1=w5=0.40
∂ E y 1 ∂ o u t a 11 = ∂ E y 1 ∂ n e t y 1 ∗ ∂ n e t y 1 ∂ o u t a 11 = 0.138498562 ∗ 0.40 = 0.055399425 \frac{\partial E_{y1}}{\partial out_{a11}}=\frac{\partial E_{y1}}{\partial net_{y1}}*\frac{\partial net_{y1}}{\partial out_{a11}}=0.138498562*0.40=0.055399425 ∂outa11∂Ey1=∂nety1∂Ey1∗∂outa11∂nety1=0.138498562∗0.40=0.055399425
同理计算出:
∂ E y 2 ∂ o u t a 11 = − 0.019049119 \frac{\partial E_{y2}}{\partial out_{a11}}=-0.019049119 ∂outa11∂Ey2=−0.019049119
两者相加得到总值:
∂ E t o t a l ∂ o u t a 11 = ∂ E y 1 ∂ o u t a 11 + ∂ E y 2 ∂ o u t a 11 = 0.055399425 + − 0.019049119 = 0.036350306 \frac{\partial E_{total}}{\partial out_{a11}}=\frac{\partial E_{y1}}{\partial out_{a11}}+\frac{\partial E_{y2}}{\partial out_{a11}}=0.055399425+-0.019049119=0.036350306 ∂outa11∂Etotal=∂outa11∂Ey1+∂outa11∂Ey2=0.055399425+−0.019049119=0.036350306
在计算 ∂ o u t a 11 ∂ n e t a 11 \frac{\partial out_{a11}}{\partial net_{a11}} ∂neta11∂outa11:
o u t a 11 = 1 1 + e − n e t a 11 out_{a11}=\frac{1}{1+e^{-net_{a11}}} outa11=1+e−neta111
∂ o u t a 11 ∂ n e t a 11 = o u t a 11 ( 1 − o u t a 11 ) = 0.59326999 ( 1 − 0.59326999 ) = 0.241300709 \frac{\partial out_{a11}}{\partial net_{a11}}=out_{a11}(1-out_{a11})=0.59326999(1-0.59326999)=0.241300709 ∂neta11∂outa11=outa11(1−outa11)=0.59326999(1−0.59326999)=0.241300709
再计算 ∂ n e t a 11 ∂ w 1 \frac{\partial net_{a11}}{\partial w_{1}} ∂w1∂neta11:
n e t a 11 = w 1 ∗ x 1 + w 2 ∗ x 2 + b 1 ∗ 1 net_{a11}=w_{1}*x_{1}+w_{2}*x_{2}+b_{1}*1 neta11=w1∗x1+w2∗x2+b1∗1
∂ n e t a 11 ∂ w 1 = x 1 = 0.05 \frac{\partial net_{a11}}{\partial w_{1}}=x_{1}=0.05 ∂w1∂neta11=x1=0.05
最后三者相乘
∂ E t o t a l ∂ w 1 = ∂ E t o t a l ∂ o u t a 11 ∗ ∂ o u t a 11 ∂ n e t a 11 ∗ ∂ n e t a 11 ∂ w 1 = 0.036350306 + 0.241300709 + 0.05 = 0.000438568 \frac{\partial E_{total}}{\partial w_{1}}=\frac{\partial E_{total}}{\partial out_{a11}}*\frac{\partial out_{a11}}{\partial net_{a11}}*\frac{\partial net_{a11}}{\partial w_{1}}=0.036350306+0.241300709+0.05=0.000438568 ∂w1∂Etotal=∂outa11∂Etotal∗∂neta11∂outa11∗∂w1∂neta11=0.036350306+0.241300709+0.05=0.000438568
更新
w
1
w_{1}
w1的权值如下:
w
1
+
=
w
1
−
η
∗
∂
E
t
o
t
a
l
∂
w
1
=
0.15
−
0.5
∗
0.000438568
=
0.149780716
w_{1}^{+}=w_{1}-\eta *\frac{\partial E_{total}}{\partial w_{1}}=0.15-0.5*0.000438568=0.149780716
w1+=w1−η∗∂w1∂Etotal=0.15−0.5∗0.000438568=0.149780716
同理,更新
w
2
w
3
w
4
w_{2}w_{3}w_{4}
w2w3w4的权值:
w
2
=
0.19956143
w_{2}=0.19956143
w2=0.19956143
w
3
=
0.24975114
w_{3}=0.24975114
w3=0.24975114
w
4
=
0.29950229
w_{4}=0.29950229
w4=0.29950229
这样误差反向传播法就完成了,最后我们再把更新的权值重新计算,不停地迭代,在这个例子中第一次迭代之后,总误差E(total)由0.298371109下降至0.291027924。迭代10000次后,总误差为0.000035085,输出为0.015912196,0.984065734,非常接近预期输出,证明效果还是不错的。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










