高级算法设计与分析 学习笔记14 FFT

​

 本章我们研究多项式乘法。

我们直接乘，时间复杂度是n^2。使用FFT则可以变成nlgn

​编辑

可以看到两个n°的多项式，我们直接乘，每种组合都要试一遍，就会要是n^2遍

​编辑

那么要怎么加速呢？

​编辑

首先多项式可以通过这种方法来表示

记录下n个点，想要原版形式的话就解矩阵方程吧。

​编辑

​编辑

​编辑

不过这种表示法太奇怪了，能不能来经典形式的？

​编辑

​

这里解释一下单位根：

单位根是复数分析中的一个概念，它是指满足以下等式的复数 ωω：

ω^n=1

这里的 n 是一个正整数，表示单位根的阶数。换句话说，单位根是一个复数，当它被提升到 n 次幂时，结果为1。单位根在复平面上的单位圆上均匀分布。

分治法！

Fn矩阵计算起来很简单：

我不明白了！还是看查特吉皮提先生讲的吧。

首先说明一下，我们的目标是把系数多项式转化成点值多项式的形式，而这个过程的核心就是要求多项式的值。多项式的结构已经写好了。

这里解释一下。这里的x=1和-1有什么特别的原因吗？：

也就是说，因为我们现在处理的子问题长度为2，那么二次单位根就是这两个。可以这么理解，原本是四次单位根的（也就是会有i,-i这些牛鬼蛇神），但是分解成子问题的时候A是有x^2来做自变量的，因此牛鬼蛇神没有了，只剩下了1和-1.当然以后遇到更复杂的可能想不明白，就记着看多项式长度就行。

子问题解决了，我们回到一开始的计算：

上面用1，-1的原因在这里再一次体现了。说白了，其实最精髓的是这些取得恰到好处的x（也就是单位根），大大减小了我们的工作量。

现在我们得到了点值形式的多项式，现在来做A(x)B(x) = C(x)的问题很简单了。：

就这样我们强行弄出了2n个点，可以表示C了。

最后通过逆FFT，得到系数多项式。这里再讲讲逆FFT是怎么做的

举个例子：

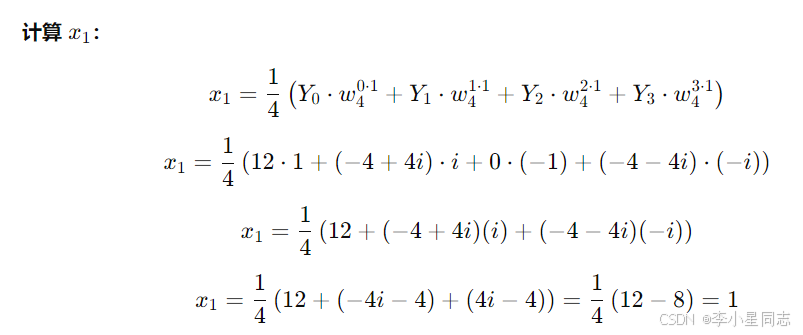
……后面省略两个。

这样，我们本章的内容就学完了。