组合数学（第三抄）鸽巢原理

最新推荐文章于 2024-12-03 22:43:29 发布

-Dong

最新推荐文章于 2024-12-03 22:43:29 发布

阅读量4k

点赞数 1

分类专栏：组合数学

本文链接：https://blog.csdn.net/LJD201724114126/article/details/81562241

版权

组合数学专栏收录该内容

19 篇文章

订阅专栏

以下大部分是搬书的，《组合数学》原书第五版。

以及有些是百度百科，我不生产算法，只是个搬运工，写着仅做方便查阅而已。

如有不妥，请留言。

一，咱首先说说鸽巢原理的简单形式：

如果要把n+1个物体放进n个盒子，那么至少有一个盒子包含两个或更多的物体。

应用1：给定m个整数a1 , a2 , ……，am，存在满足 $0\leq k< l\leqslant m{\color{Blue} }$ 的整数 k 和 l，使得 $_a{k+1}+_a{k+2}+……+_a{l}$ …… $+_a{l}$ 能够被m整除。通俗的地说，就是在序列a1，a2，……，am中存在连续的a，使得这些a的和能够被m整除。

证明：考虑m个和

a1,a1+a2,a1+a2+a3,……,a1+a2+a3+...+am

如果这些和当中的任意一个可被m整除，那么结论就成立。因此，我们可以假设这些和中的每一个除以m都有一个非零余数，余数等于1,2，……，m-1 中的一个数。因为有m个和，而只有m-1个余数，所以必然有两个和除以m有相同的余数。因此，存在整数 k和 l，k<l，使得a1+a2+...+ak 和 a1+a2+...+al除以m有相同的余数r：

a1+a2+...+ak=b*m+r，a1+a2+...+al=c*m+r

二式相减，发现 $_a{k+1}+_a{k+2}+……+_a{l}$ ... $+_a{l}$ =（c-b）*m，从而 $_a{k+1}+_a{k+2}+……+_a{l}$ ... $+_a{l}$ 能够被m整除。

举个例子：设m=7，且整数为 2,4,6,3,5,5,6 。计算上面的和得到 2,6,12,15,20,25,31，这些整数被7除时余数分别为 2,6,5,1,6,4,3。有两个等于6的余数，这意味着结论：6+3+5=14 可被7整除。

题目1：hdu 1808

题目大意：

给你两个整数C和N，再给你N个正数的序列，从中找到若干数，使得其和刚好是 C

的倍数。输出这些数的序号。

我们知道C<=N的，故我们可以用鸽巢原理去做，

思路：

Sum[i]为序列中前 i 项的和。则有两种可能：

1.若有 Sum[i] 是 C 的倍数，则直接输出前 i 项。

2.如果没有任何的 Sum[i] 是 C 的倍数，则计算 ri = Sum[i] % C。根据鸽巢原理，肯

定有 Sum[i] % C == Sum[j] % C，j<i。则第 j +1项到第 i 项数的和即为 C 的倍数。

这题说，要是没答案就输出 “no sweets” ，想想，这有可能吗？

///鸽巢原理，因为c<=n,故可以用鸽巢原理去做，要c>n就不行了
#include<cstdio>
#include<algorithm>
#include<cstring>

using namespace std;

const int maxn=100010;

int num[maxn],sum[maxn],mod[maxn];

int main()
{

    int c,n,right,left;
    while(~scanf("%d%d",&c,&n)&&(c||n))
    {

        memset(mod,-1,sizeof(mod));///存储mod值的下标
        memset(sum,0,sizeof(sum)); ///存储前k项和mod c后的值



        mod[0]=0;///此处是判断前k项和就是c的倍数，特殊处理

        for(int i=1;i<=n;i++)
        {
            scanf("%d",&num[i]);

            sum[i]=(sum[i-1]+num[i])%c;

            if(mod[sum[i]]==-1){
                mod[sum[i]]=i;
            }
            else {
                left=mod[sum[i]];
                right=i;
            }
        }

        for(int i=left+1;i<right;i++)
            printf("%d ",i);
        printf("%d\n",right);


    }
    return 0;
}

题目二：hdu 1205

题解：我们首先计算出总糖果数sum和某一种最大数量的糖果数maxs，

这时就可以分两种情况讨论，1，假设maxs-1<=sum，答案是Yes，反之为No。

为什么呢？我们可以想下，某一种糖果数位maxs，要使得这些相同糖果b不能相邻，那是不是至少需要maxs-1个其它糖果a把这些相同糖果b隔绝掉，所以答案就出来了。

应用2：

从整数1,2,...,200中选出101个整数。证明：在所选的这些整数之间存在两个这样的整数，其中的一个可被另一个整除。

首先要先知道这点：任一整数都可以写成 $2^{k}*a{\color{Red} }$ 的形式，其中k>=0&&a是奇数。

对于1到200之间的一个整数，a是100个数1,3,5，...，199中的一个。因此，在所选的101个整数中存在两个整数，当写成上述形式时这两个数具有相同的a值。令这两个数是2^r*a和2^s*a，如果r<s,那么第二个数就能被第一个数整除。反之亦然。

注意，从1,2，...，200中可以选择100个数，使得其中没有一个能被另一个数整除（比如，这100个整数是101,102，...，119,200）

鸽巢原理加强版：

定理：设q1，q2，...，qn是正整数。如果将 q1+q2+...+(qn)- n+1 个物体放入n个盒子内，那么或者第一个盒子至少含有q1个物体，或者第二个物体至少含有q2个物体，...，或者第n个物体至少含有qn个物体。

证明略，自己看书或者网上。

推论：

设n和r都是正整数。如果把 n(r-1)+1 个物体分配到n个盒子中，那么至少有一个盒子含有r个过更多的物体。

平均原理：

如果n个非负整数 m1,m2,...,mn 的平均数大于 r-1 ，即

$\frac{ m1+m2+..+mn }{n}> r-1$ , 那么至少有一个整数大于或等于 r 。

如果n个非负整数 m1,m2,...,mn 的平均数小于 r-1 ，即

$\frac{ m1+m2+..+mn }{n}<r-1$ , 那么至少有一个整数小于 r 。

接下来我们隆重介绍下鸽巢原理的扩展，

Ramsey定理：在6个（或更多的）人中，或者有三个人，他们中的每两个人都相互认识，或者有3个人，他们中的每两个人都互相不认识。

抽象表示为 K6 -> K3,K3（读作K6箭指K3,K3）。

Kn表示n个对象和这些对象中每两个对象配成的对。

K6->K3,K3 是这样的一个论断：不管用红色和蓝色如何去着色K6的边，总存在一个红K3（原始的6个点中有3个点，它们之间的3条线段均被着成红色）或蓝3（原始的6个点中有3个点，它们之间的3条线段均被着成蓝色），总言之，总存在一个单色三角形。

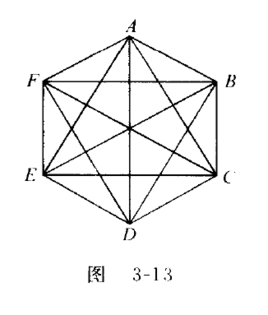
证明如下：首先，把这6个人设为A、B、C、D、E、F六个点。由A点可以引出AB、AC、AD、AE、AF五条线段。设：如果两个人认识，则设这两个人组成的线段为红色；如果两个人不认识，则设这两个人组成的线段为蓝色。

由抽屉原理可知：这五条线段中至少有三条是同色的。不妨设AB、AC、AD为红色。若BC或CD为红色，则结论显然成立。若BC和CD均为蓝色，则若BD为红色，则一定有三个人相互认识；若BD为蓝色，则一定有三个人互相不认识。

定理1：如果m>=2及n>=2是两个整数，则存在正整数p，使得

Kp->Km,Kn。

设Ramsey数r（m,n）是使Kp->Km,Kn成立的最小整数p。

显然r（m,n）=r(n,m)。

对于r（2,n）=n, r(m,2)=m，（m,n>=2）这些数被称为平凡数。

证明下r（2,n）：

r(2,n)<=n，事实上，如果把Kn的边或者着成红色或者着成蓝色，那么，或者Kn的某条边是红色的（因此就得到一个红K2），或者Kn所有的边都是蓝色的（因此就得到了一个蓝Kn）。

相关定理

定理1：R(a,b)=R(b,a), R(a,2)=a

定理2：对任意整数a,b>=2, R(a,b)存在。

定理3：对所有的整数a,b

R(a,b)<=R(a-1,b)+R(a,b-1)

定理4：对所有的整数a和b，a,b>=2，若R(a,b-1)和R(a-1,b)是偶数，则

R(a,b)<=R(a-1,b)+R(a,b-1)-1

定理5对于a,b>=2,有

R(a,b)<=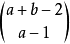

题目：hdu 5917

题意：给你n个点，m条边，然后告诉你选择一个点集S
如果里面有一个子集A，A里面的点都不相连，或者都相连，则这个点集不稳定
求不稳定的个数。

题解：子集A的大小是大于等于3，所以考虑到6个点的图，里面肯定有3个点，互相有边，或者互相没边
所以用ramsey定理优化，6以上都可以直接求。ans = pow(2,n) - C(n,i) i属于[ 0 , 5 ]
剩下3，4，5的情况，直接暴力计算[ 3 , 5 ]的点集里哪些属于合法的即可。

代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;

const int M = 1e2+7;
const LL mod = 1e9+7;

int ncase,n,m,cas=1;
int vis[M][M];
LL fac[M];

void init(){///预处理阶乘
    fac[0]=1;fac[1]=1;
    for (int i=2;i<M;i++)
    {
        fac[i]=fac[i-1]*i%mod;
    }

}

LL quick_pow(LL p,LL k)///快速幂
{
    LL res=1,tp=p;
    if(k<0) return 0;
    while(k){
        if(k&1) res=res*tp%mod;
        tp=tp*tp%mod;
        k>>=1;
    }
    return res;
}
LL C(int n,int m){///费马小定理求逆元+快速幂
    return fac[n]*quick_pow(fac[m],mod-2)%mod*quick_pow(fac[n-m],mod-2)%mod;
}
int judge(int i,int j,int k){///判断三点之间满不满足不稳定点集

    if(vis[i][j]&&vis[i][k]&&vis[j][k]) return 1; ///三点之间相连
    if(!vis[i][j]&&!vis[i][k]&&!vis[j][k]) return 1;///三点之间不互联
    return 0;
}
int judge1(int i,int j,int k,int l){
    if(judge(i,j,k)||judge(i,j,l)||judge(j,k,l)||judge(i,k,l)) return 1;
    ///表示4个点中有三个点为不稳定点集就行,为什么呢？
    ///因为时题目要求的，不稳定点集为3个点。

    return 0;
}
int judge2(int i,int j,int k,int l,int o){
    ///表示5个点中有4个点满足就行

    if(judge1(i,j,k,l)||judge1(i,j,k,o)||judge1(i,j,l,o)||judge1(j,k,l,o)||judge1(i,k,l,o)) return 1;
    return 0;
}
int main(){

    init();
    scanf("%d",&ncase);
    while(ncase--){
        scanf("%d%d",&n,&m);
        memset(vis,false,sizeof(vis));

        for(int i=1;i<=m;i++){
            int u,v;
            scanf("%d%d",&u,&v);
            vis[u][v]=vis[v][u]=1;
        }
        LL ans=0;

        if(n>=6){
            ans=(ans+quick_pow(2,n))%mod;
            ///多项式定理C(n,0)+C(n,1)+...+C(n,n)=2^n
            ///C(n,k)(k>=6)表示，从n个中取k个出来，总存在一个不稳定点集的个数（三点之间互联或三点之间不连）

            for(int i=0;i<6;i++)///减去前5个
                ans=(ans-C(n,i)+mod)%mod;
        }
        if(n>=3){///暴力取3个

            for(int i=1;i<=n;i++)
                for(int j=i+1;j<=n;j++)
                    for(int k=j+1;k<=n;k++)
                        if(judge(i,j,k)) ans=(ans+1)%mod;
        }
        if(n>=4){///暴力取4个

            for(int i=1;i<=n;i++)
                for(int j=i+1;j<=n;j++)
                    for(int k=j+1;k<=n;k++)
                        for(int l=k+1;l<=n;l++)
                            if(judge1(i,j,k,l)) ans=(ans+1)%mod;
        }
        if(n>=5){///暴力取5个

            for(int i=1;i<=n;i++)
                for(int j=i+1;j<=n;j++)
                    for(int k=j+1;k<=n;k++)
                        for(int l=k+1;l<=n;l++)
                            for(int o=l+1;o<=n;o++)
                                if(judge2(i,j,k,l,o)) ans=(ans+1)%mod;
        }
        printf("Case #%d: %lld\n",cas++,ans);
    }
    return 0;
}

第四篇：组合数学（第四抄）

我的标签：做个有情怀的程序员。