组合数学知识点汇总

组合数学

第 1 章 排列、组合、二项式定理

1.2 排列与组合

1.2.1 集合的排列

注：r圆排列数不要和组合数搞混了

1.2.2 集合的组合

1.3 多重集合的排列与组合

1.3.1 多重集合的排列

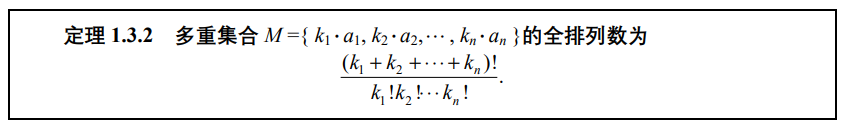
1.3.2 多重集合的组合

注：这里是无限多重集合，2.2.1介绍了如何求任意重集合的r组合数

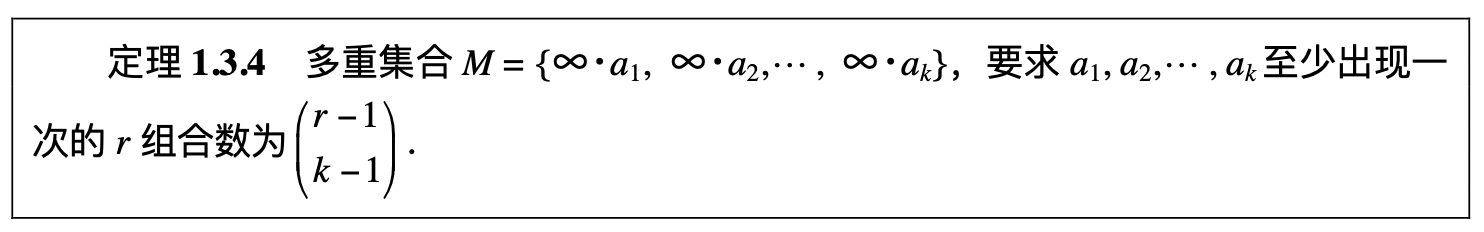
1.4 二项式定理

1.4.1 二项式定理的证明

1.4.2 二项式系数的基本性质

1.4.3 组合恒等式

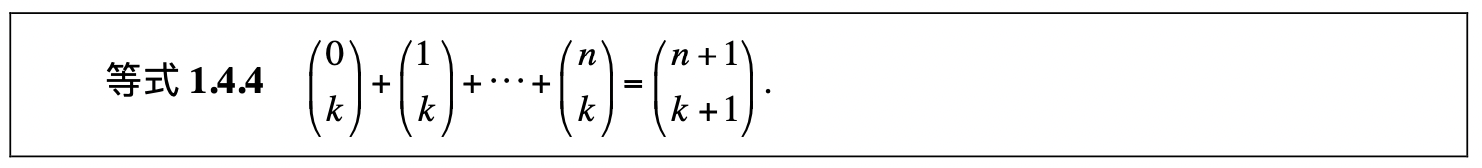
1.4.4 多项式定理

1.5 集合的分划与第 2 类 Stirling 数

1.6 正整数的分拆

1.6.1 有序分拆

1.6.2 无序分拆

1.6.3 分拆的 Ferrers 图

不考

1.7 分配问题*

1.8 习题

第 2 章 容斥原理与鸽巢原理

2.1 容斥原理

2.1.2 容斥原理的 3 个形式

2.1.3 应用举例

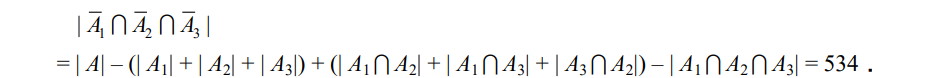
2.2 容斥原理的应用

2.2.1 具有有限重复数的多重集合的 r 组合数

不是很懂

2.2.2 错排问题

集合{1, 2, …, n}的一个错排是该集合的一个满足条件 i ≠ j 的全排列 $i_1{i}_2\dots i_n$，即集合{1, 2, …, n}的没有一个数字在它的自然顺序位置上的全排列。

2.2.3 有禁止模式的排列问题

2.2.4 n 对夫妻问题（ménage）

没看

2.3 Möbim 反演

不考

2.4 鸽 巢 原 理

2.4.2 鸽巢原理的形式

2.5 Ramsey 问题与 Ramsey 数

不考

2.6 习 题

第 3 章 递 推 关 系

3.1 递推关系的建立

3.2 常系数线性齐次递推关系的求解

easy

easy~

3.3 常系数线性非齐次递推关系的求解

3.4 用迭代法求解递推关系

3.5 Fibonacci 数和 Catalan 数

3.6 习 题

第 4 章 生 成 函 数

]

[外链图片转存中…(img-PFFj6NKj-1640185573123)]

[外链图片转存中…(img-ijJKBT0Q-1640185573123)]

[外链图片转存中…(img-rD1hlauk-1640185573123)]

3.4 用迭代法求解递推关系

3.5 Fibonacci 数和 Catalan 数

3.6 习 题

第 4 章 生 成 函 数