【c++/数据结构】红黑树-RBTree

最新推荐文章于 2024-05-14 19:44:49 发布

LLZK_

最新推荐文章于 2024-05-14 19:44:49 发布

阅读量1.2k

点赞数 1

分类专栏： c/c++ 数据结构 c++/数据结构文章标签：红黑树旋转操作红黑树插入调整算法 RBTree 数据结构

本文链接：https://blog.csdn.net/LLZK_/article/details/52972163

版权

红黑树是一种近似平衡的二叉搜索树，保证最长路径不超过最短路径的两倍。插入操作可能导致不平衡，需要通过颜色调整和旋转操作恢复平衡。文章详细介绍了插入情况1、2、3的处理方式，包括颜色变化和旋转操作，确保路径上黑色节点数量不变。

摘要由CSDN通过智能技术生成

什么叫红黑树？

同AVL树一样，红黑树也是近似平衡的二叉搜索树，与AVL树不同的是红黑树没有了平衡因子，但增加了一个枚举变量，来标明结点的颜（RED or BLACK）。因为红黑树可以保证它的最长路劲不超过它最短路径的两倍，所以它近似平衡。

红黑树具有以下几点性质：
1. 每个结点都必须具有一种颜色（RED or BLACK）。
2. 根结点为黑色。
3. 如果一个结点为红色，那么它的两个孩子结点均为黑色（没有连续的红结点）。
4. 对于每个结点，该结点到其所有后代叶子结点的路径上，黑色结点的数量相同。
5. 每个空结点（NIL结点）都当作一个黑色结点。

下图为一棵简单的红黑树：
这里写图片描述

如何去创建并维护一棵红黑树？

红黑树的难点与AVL树相同，插入一个结点并不难，难点在于插入一个结点后，很容易破坏这棵树的平衡，我们就需要做一些调整工作让这棵树恢复平衡。
那么什么时候需要我们做调整工作呢？看上面红黑树性质第三点，一棵红黑树需要满足没有连续的红结点。
需要调整的两种情况：
1. 当我们对一个红结点下插入一个红结点时，出现了连续的红结点。调整。
2. 调整需要改变结点的颜色，当我们把一个黑结点变为红结点，而恰好这个结点的父亲是一个红结点。又出现了连续的红结点。继续调整。

同时，性质第4点也很重要，对于每个结点，该结点到其所有后代叶子结点的路径上，黑色结点的数量相同。当我们对一棵子树进行调整，这棵子树也可能拥有一棵兄弟子树，所以我们不能改变当前子树上黑色节点的数量，即路径上黑结点的数量不能改变。
总结下来，调整方案就是：遇到连续红结点就调整，调整的同时要保证路径上黑色节点的数量不变。

PS：①在下面的讲解中会改变结点的颜色，当我们遇到连续的红结点并进行调整时，我们并不知道这个红结点怎么来的，可能是新插入的，也可能是之前的调整由黑结点变过来的。②叔叔结点（uncle）。③a、b、c、d、e均为子树，若一个为空，则都为空，此时cur为新插入结点。若不为空，则都不为空，此时cur为被调整改变的结点。注意这个三个概念，会帮助我们理解下面的讲解。

插入情况1：

当前结点cur为红，父亲结点parent为红，gparent为黑，叔叔结点uncle存在且为红。
①
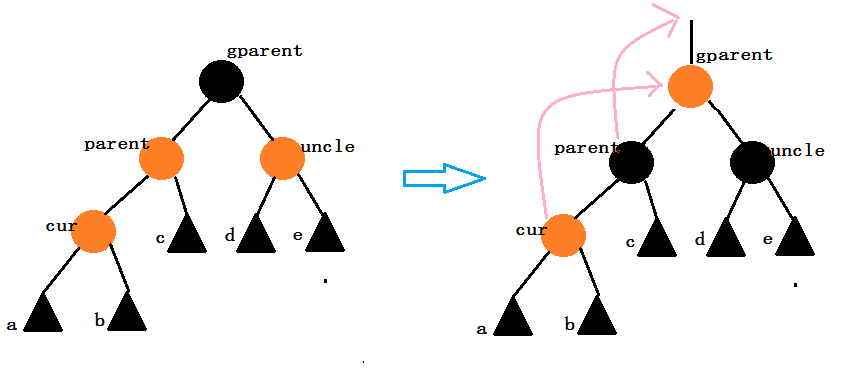
这里写图片描述
②

这种情况我们只需要改变结点颜色，不需要挪动结点位置。
颜色调整：将parent与叔叔结点uncle的颜色变为黑色，将gparent的颜色变为红色。
继续向上调整：令cur = gparent，parent = gparent->_parent。继续向上调整。

代码

uncle->_col = parent->_col = BLACK;
Gparent->_col = RED;// Gparent 可能为子树，保证黑色节点数量不变

//继续向上调整
cur = Gparent;
parent = cur->_parent;

插入情况2：

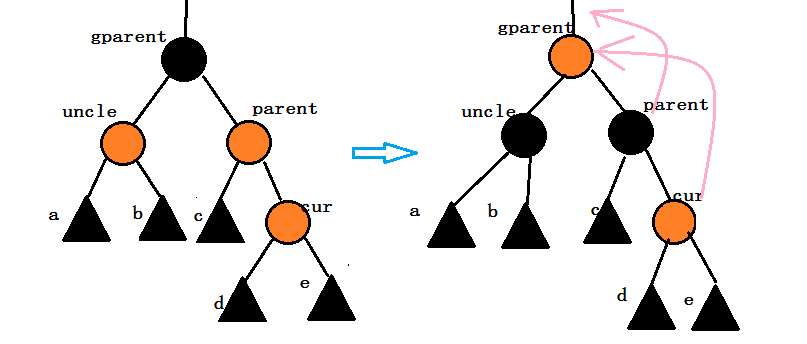
当前结点cur为红色，parent为红色，gparent为红色，叔叔结点uncle不存在或者为黑。(ps：当uncle结点不存在时，所有子树都不存在，cur为新插入结点，当uncle存在且为黑时，cur为被调整改变的结点。以下我们以uncle存在且为黑为例。)

这个情况又可分为两种小情况：
① parent为gparent的左孩子，cur为parent的左孩子。
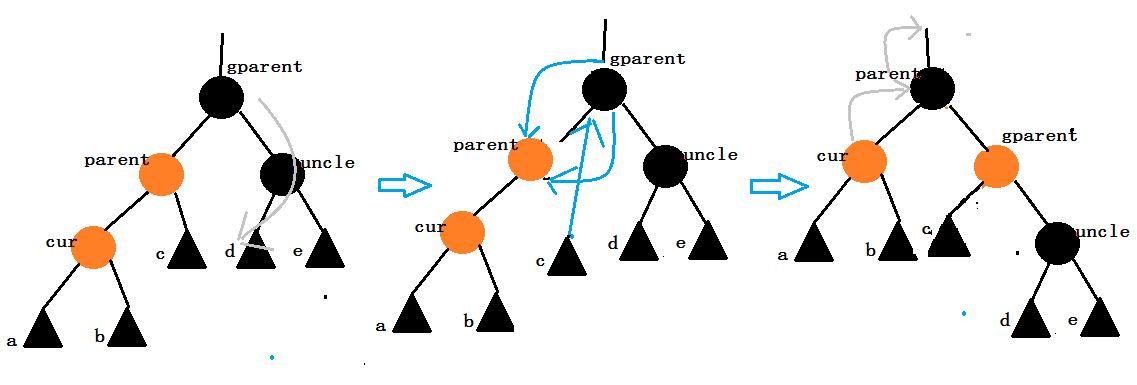
这里写图片描述
这种情况需要对gparent进行右单旋操作，看过之前我写的AVL树讲解的朋友们相信已经对旋转操作不再陌生了，这里我再讲一下。
旋转操作：将parent的右子树变成gparent的左子树，将gparent以及其子树变成parent的右子树。将gparent的父亲结点指向parent。
颜色调整：将parent的颜色变成黑色，将gparent的颜色变成红色。
继续向上调整：令cur = parnet， parent = parent->_parnet.

代码：

void RotateR(Node* parent)
{
    Node* SubL = parent->_left;
    Node* SubLR = SubL->_right;
    parent->_left = SubLR;

    if (SubLR)
    {
        SubLR->_parent = parent;
    }

    Node* ppNode = parent->_parent;

    SubL->_right = parent;
    parent->_parent = SubL;

    if (ppNode)
    {
        if (ppNode->_left == parent)
            ppNode->_left = SubL;
        else
            ppNode->_right = SubL;
        SubL->_parent = ppNode;
    }
    else
    {
        SubL->_parent = NULL;
        _root = SubL;
    }
}

② parent为gparent的右孩子，cur为parent的右孩子。
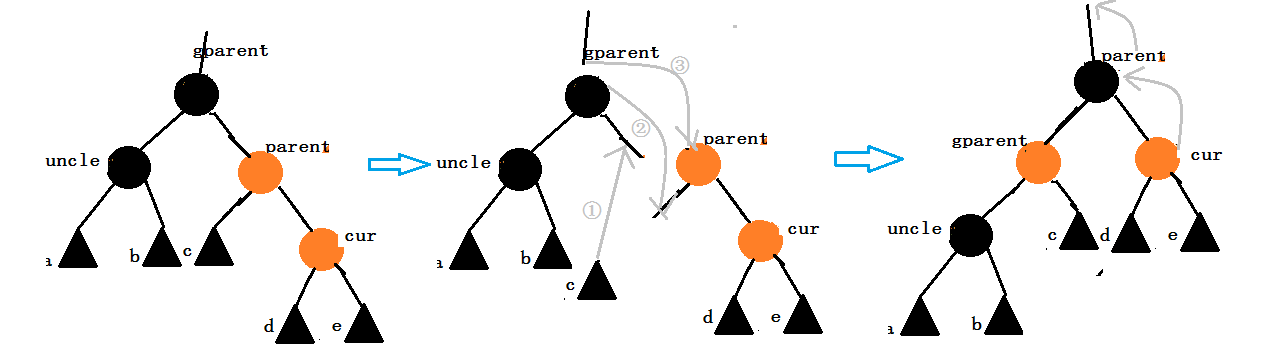
这里写图片描述
这种情况需要对gparent进行左单旋操作。
旋转操作：将parent 的左子树变为gparent的右子树，将gparent以及其子树变成parent的左子树，将gparnet的父亲结点指向parent。
颜色调整：将parent变为黑色，将gparent变为红色。
继续向上调整：令cur = parent，parent = parent->_parent。