决策树（Decision Tree）

决策树算法是一种基于决策的预测算法，顾名思义，每一个决策相当于一棵树的枝干，而每个枝干都会导向一个决策结果。

决策树其实可以分为分类树和回归树，分类树是指输出每个样本的类别，而回归树是指输出数值结果，这里我们只讨论分类树。

在应用中，决策树通常是基于一套规则去将数据分门别类。在一个数据集中，决策树算法会利用每一个样本的属性变量，并确定哪一个属性是最重要的，然后给出一系列决策去最优地将数据划分成多个子集。

创建一个决策树的过程是递归的，对于一个数据集Ｓ，运用决策树的流程如下：

　　１、如果Ｓ中的所有样本都归属于同一个类别或者Ｓ非常小，那么决策树就只有一个节点，并且这个节点被决策为那个最多的类别，结束划分子集；
　　２、如果Ｓ很大并且样本归属的类别不止一个，那么需要找到一套最优的规则去将样本分类；
　　３、对于划分好的子集，重复进行上述第１、２步。

最常见的决策树是在游戏“猜谜语”中，例如下面一段对话就是一个很好的例子：
　　
　　Ａ：打一动物。
　　Ｂ：它有超过两条腿吗？
　　Ａ：没有。
　　Ｂ：它会下蛋吗？
　　Ａ：会。
　　Ｂ：它美味吗？
　　Ａ：是。
　　Ｂ：它会打鸣吗？
　　Ａ：会。
　　Ｂ：它是公鸡吗？
　　Ａ：是。

显而易见，这个决策树的流程就是：

决策树的应用场景很多，并且它是很容易理解的，决策的过程对外也是透明的，而不像其他的例如神经网络分类器，看起来似乎是一个暗箱。决策树很容易处理一系列数值属性（如几条腿）和类别属性（如是否美味），甚至可以处理属性丢失的数据情形。

如何创建一个最优的决策树呢？要回答这个问题，我们得首先明白怎么去划分子集，划分子集的最直接缘由就是最大可能性地将数据划分，而从数学上去理解的话就是使得信息熵最小。

好比打字谜游戏，提出一个好的问题能够迅速地找到谜底。为了构建一个决策树，我们需要去确定如何提问以及如何安排这些问题的顺序。每一个问题都会包含一部分可能性，而每个答案都会去对数据进行划分可能性。

熵在物理中是指混乱程度，在这里的含义是包含信息量的多少，信息量就是不确定性或者可能性。例如“明天是星期三”所包含的信息量非常小，因为这个是确定的；而“明天北京下雨的概率是2/5”所包含的信息量较大，因为它给出了可能性。

设想我们有一个数据集，每一个样本都有一个确定的类别标签。如果所有样本都同属于某一个标签，那么此时的不确定性就没有了，也就是我们所说的熵很低；而如果所有样本所属的标签均匀分布，贯穿所有，那么此时就有了很多不确定性，我们认为此时的熵很高。

数学上，如果一个样本被预测为属于类别C_i的概率为P_i，那么可以定义熵的公式为：
H(S)=-P_1*log(P_1)-...-P_n*log(P_n)

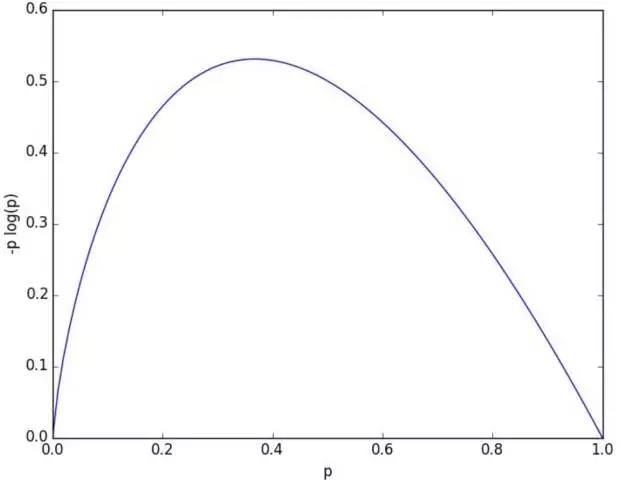
H(S)中的每一项都是非负的，因此最终结果也是非负的，为了使得H(S)最大化，我们可以作出-P*log(P)的图像，来看看Ｐ的大小如何影响-P*log(P)的值。

从图像可以看出，当Ｐ接近于０或者１时，-P*log(P)的值最小，即熵最低。而Ｐ＝０或Ｐ＝１恰好对应概率中的确定事件，即某个事件一定发生或一定不发生；当Ｐ处在０和１之间时，熵相对较高。

在决策树中，每当我们提出一个问题时，如果答案对我们划分数据的类别的确定性较大，那么这种划分的熵就很小；反之，如果答案对我们划分数据的类别的不确定性仍然较大，那么这种划分的熵就很大。

数学上，如果把一个大数据集划分成S_1,...,S_m,并且每部分所占总数据集的比例为q_1,...,q_m，那么我们计算出划分的总加权熵为：
H=q_1*H(S_1)+...+q_m*H(S_m)

接下来我们会根据划分熵来构建一个决策树。例如现在有一个关于14个应聘者简历的数据集，我们需要根据简历来筛选应聘者。简历有四个属性，分别是水平、语言、社交活跃、博士学位，为了便于分析，我们对每个属性的取值较少。预测的结果只有两种情况：是否招聘。我们可以根据前面提到的决策树贪婪流程去将应聘者分类。

既然有四个属性用于分类，那么我们第一步要做的就是找到那个使得划分熵最小的划分属性。

对于【水平】属性而言，其中初级占5/14，中级占4/14，高级占5/14；每个初级被招聘的概率为2/5，每个中级被招聘的概率为4/4，每个高级被招聘的概率为2/5，因此对于【水平】属性的划分熵为：H(水平)=5/14 *(-2/5 *log(2/5))+4/14 *(-1 *log(1))+5/14 *(-2/5 *log(2/5))=0.1137

对于【语言】属性而言，其中Java占3/14，Python占7/14，R占4/14；每个Java被招聘的概率为1/3，每个Python被招聘的概率为5/7，每个Ｒ被招聘的概率为3/4，因此对于【语言】属性的划分熵为：H(语言)=3/14*(-1/3*log(1/3))+7/14*(-5/7*log(5/7))+4/14*(-3/4*log(3/4))=0.0777+0.1202+0.0616=0.2595

对于【社交活跃】属性而言，其中是占7/14，否占7/14；每个是被招聘的概率为6/7，每个否被招聘的概率为3/7，因此对于【社交活跃】属性的划分熵为：H(社交活跃)=7/14*(-6/7*log(6/7))+7/14*(-3/7*log(3/7))=0.0661+0.1816=0.2477

对于【博士学位】属性而言，其中是占6/14，否占8/14；每个是被招聘的概率为3/6，每个否被招聘的概率为6/8，因此对于【博士学位】属性的划分熵为：H(博士学位)=6/14*(-3/6*log(3/6))+8/14*(-6/8*log(6/8))=0.1485+0.1233=0.2718

因此，就第一步的划分熵而言，H(水平)<H(社交活跃)<H(语言)<H(博士学位)，因此，决策树第一步按照划分熵最小原则，取水平作为第一步划分依据。党我们把数据集划分为初级、中级、高级三个子集时，我们可以接着对它们的语言、社交活跃、博士学位计算划分熵，然后再确定每个子集的最小划分熵。这里就不多解释了，计算步骤同上。

根据划分熵最小原理，我们就能一步步得出一个筛选简历的决策树系统。当然实际中，我们要把数据集分为训练集和测试集，根据测试误差去优化决策树模型。

决策树的优点是很容易理解，决策过程透明，并且代码易写，而且将属性之间的非线性关系变得更加直观，预测速度较快。

决策树的缺点是不稳定，受数据的噪音影响较大，并且决策的边界分明且平行。如果想要决策边界不那么分明，Ensemble-Lerning或最近邻算法是个不错的选择（K-最近邻算法的应用）；如果想要决策边界并非平行的，支持向量机或逻辑回归是个不错的选择。

对于训练数据，如果我们的决策树模型拟合地很精细，那么很容易导致过拟合了