【数据结构】中的计数排序(CountSort)

计数排序的概念：

      1.计数排序的原理：设被排序的数组为A,排序后存储到B，C为临时数组。所谓计数，首先是通过一个数组C[i]计算大小等于i的元素个数，此过程只需要一次循环遍历就可以；在此基础上，计算小于或者等于i的元素个数，也是一重循环就完成。下一步是关键：逆序循环，从length[A]到1，将A[i]放到B中第C[A[i]]个位置上。原理是：C[A[i]]表示小于等于a[i]的元素个数，正好是A[i]排序后应该在的位置。而且从length[A]到1逆序循环，可以保证相同元素间的相对顺序不变，这也是计数排序稳定性的体现。在数组A有附件属性的时候，稳定性是非常重要的。

     2.计数排序的前提及适用范围:A中的元素不能大于k,而且元素要作为数组的下标，所以元素应该为非负整数。而且如果A中有很大的元素，不能够分配足够大的空间。所以计数排序有很大局限性，其主要适用于元素个数多，但是普遍不太大而且总小于k的情况，这种情况下使用计数排序可以获得很高的效率。

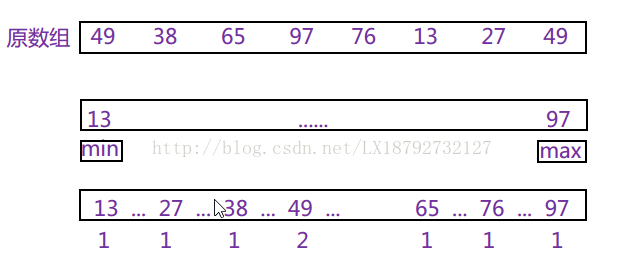
计数排序算法的基本思想是对于给定的输入序列中的每一个元素x，确定该序列中值小于x的元素的个数。一旦有了这个信息，就可以将x直接存放到最终的输出序列的正确位置上。例如，如果输入序列中只有17个元素的值小于x的值，则x可以直接存放在输出序列的第18个位置上。

如下图所示：

实现计数排序的代码：

#include<iostream>
using namespace std;
#include<assert.h>
#pragma once

void CountSort(int *a, size_t n)
{
	assert(a);
	int max = a[0];
	int min = a[0];
	for (size_t i = 0; i < n; ++i)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
		if (a[i] < min)
		{
			min = a[i];
		}
	}
	int range = max - min + 1;
	int *Counts = new int[range];
	memset(Counts, 0, sizeof(size_t)*range);

	for (size_t i = 0; i < n; ++i)
	{
		Counts[a[i] - min]++;
	}
	size_t j = 0;

	for (size_t i = 0; i < n; ++i)
	{
		while (Counts[i]--)
		{
			a[j++] = i + min;
		}
	}
	delete[] Counts;
}
void printArray(int *a, size_t n)
{
	for (size_t i = 0; i < n; i++)
	{
		cout << a[i] << " ";
	}
	cout << endl;
}
int main()
{
	int arr[] = { 1, 3, 5, 7, 0, 2, 9, 4, 6, 2 };
	//int arr[] = { 4, 38, 65, 97, 76, 13, 27, 49 };
	int n = sizeof(arr) / sizeof(arr[0]);
	cout << "进行计数排序前：";
	printArray(arr, n);
	CountSort(arr, n);
	cout << "进行计数排序后：";
	printArray(arr, n);
	system("pause");
	return 0;
}

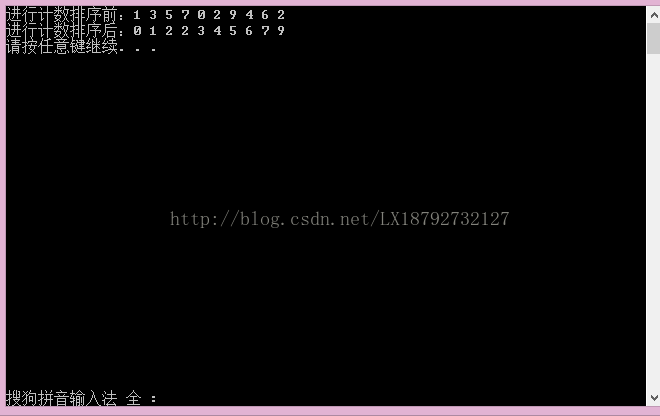
运行的结果：