
这题样例理解了模拟就行,不要想太复杂
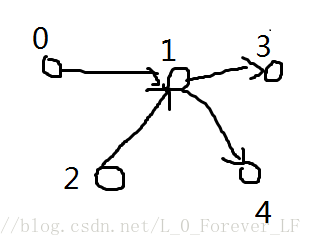
样例给出了
0−>1−>3,2−>1−>3,2−>1−>4
三条边,但是构造出的图还应有
0−>1−>4
,所以无解
然后可以得出一个结论,对于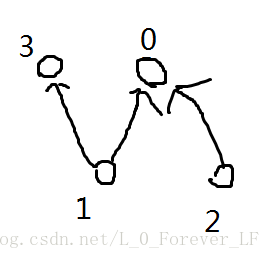
code:
#include<set>
#include<map>
#include<deque>
#include<queue>
#include<stack>
#include<cmath>
#include<ctime>
#include<bitset>
#include<string>
#include<vector>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<climits>
#include<complex>
#include<iostream>
#include<algorithm>
#define ll long long
using namespace std;
const int maxm = 210000;
const int maxn = 310;
struct edge
{
int y,nex;
edge(){}
edge(int _y,int _nex){y=_y;nex=_nex;}
}a[maxm]; int len,fir[maxn];
int u[maxn][maxn],ul[maxn],o[maxn];
int n,m;
void ins(int x,int y)
{
len++;
a[len].y=y;
a[len].nex=fir[x]; fir[x]=len;
}
bool v[maxn];
int glen;
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
memset(fir,0,sizeof fir); len=0;
memset(o,0,sizeof o);
memset(ul,0,sizeof ul);
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int x,y; scanf("%d%d",&x,&y); x++; y++;
ins(x,y); u[y][++ul[y]]=x;
o[x]++;
}
bool flag=true;
for(int i=1;i<=n;i++)
{
if(ul[i]>1)
{
memset(v,false,sizeof v);
int x=u[i][1];
glen=o[x];
for(int k=fir[x];k;k=a[k].nex)
v[a[k].y]=true;
for(int j=2;j<=ul[i];j++)
{
x=u[i][j];
if(o[x]!=glen) {flag=false; break;}
for(int k=fir[x];k;k=a[k].nex)
if(!v[a[k].y]) {flag=false; break;}
if(!flag) break;
}
}
if(!flag) break;
}
if(flag) printf("Yes\n");
else printf("No\n");
}
return 0;
}























 550
550

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








