稀疏矩阵的特点
M*N矩阵,矩阵中有效值的个数远远小于无效值的个数,并且这些数据的分布没有规律。
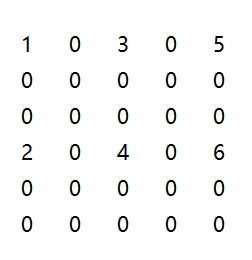
例如下面的矩阵
稀疏矩阵的压缩存储
压缩矩阵值存储极少数的有效数据。使用三元组来存储每一个数据,三元组数据按照矩阵中的位置,以行优先顺序依次存放。
则上述矩阵的存储结构为
三元组结构
//三元组的定义
template<class T>
struct Triple
{
public:
//默认无参构造函数
Triple()
{}
//构造函数
Triple(const T& d,size_t row=0,size_t col=0)
:_value(d)
,_row(row)
,_col(col)
{}
public:
T _value;//数据域
size_t _row;//行
size_t _col;//列
};稀疏矩阵的压缩
template<class T>
class SparseMatrix
{
public:
//无参构造函数
SparseMatrix()
{}
SparseMatrix(const T* a, size_t row, size_t col, const T& invalid);
void Display();//打印
SparseMatrix<T> Transport();//列转置
SparseMatrix<T> FastTransport();//快速转置
private:
vector<Triple<T>> _a;//三元组类型的顺序表
size_t _rowSize;//行数
size_t _colSize;//列数
T _invalid;//非法值
};
//矩阵的压缩
template<class T>
SparseMatrix<T>::SparseMatrix(const T* a, size_t row, size_t col, const T& invalid)
:_rowSize(row)
, _colSize(col)
, _invalid(invalid)
{
//行遍历
for (size_t i = 0; i < row; i++)
{
//列遍历
for (size_t j = 0; j < col; j++)
{
if (a[i*col + j] != invalid)
{
_a.push_back(Triple<T>(a[i*col + j], i, j));
//不能通过数组创建,但是可以通过数组形式访问
}
}
}
}转置
将原矩阵的行、列互换,也就是将[row][col]和[col][row]位置上的数据对换。
列转置
算法思想:
采用按照被转置矩阵三元组表A的序列(即转置后三元组表B的行序)递增的顺序进行转置,并以此送入转置后矩阵的算远足表B中,这样一来,转置后矩阵的三元组表B恰好是以“行序为主序的”.
实现代码
//列转置
template<class T>
SparseMatrix<T> SparseMatrix<T>::Transport()
{
SparseMatrix<T> result;
//行列size互换
result._rowSize = _colSize;
result._colSize = _rowSize;
result._invalid = _invalid;
//按照列扫描
for (size_t j = 0; j < _colSize; j++)
{
//在三元组数组中找到相同列的元素
for (size_t index = 0; index < _a.size(); index++)
{
if (_a[index]._col == j)
{
result._a.push_back(Triple<T>(_a[index]._value, _a[index]._col, _a[index]._row));
//按照列优先的顺序存到压缩数组中
}
}
}
return result;
}算法分析:
算法的时间主要消耗在双重循环中,其时间复杂度为O(_colSize*_a.size)。
一次定位快速转置
算法思想:
在列转置中算法的时间浪费主要在双重循环中,要改善算法的性能,必须去掉双重循环,使得整个转置过程通过一次循环来完成。
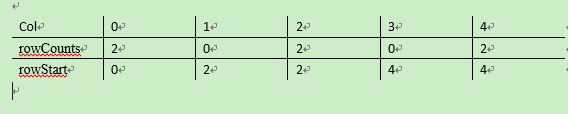
为了能使得被转置的三元组表A中元素一次定位到三元组表B中,需要预先计算一下数据:
1)rowCounts,三元组表A中每一列有效值的个数,即转置后矩阵三元组表B中每一行有效值的个数。
2)rowStart,三元组表B中每一行有效值的起始位置。
rowStart[col]=rowStart[col-1]+rowCounts[col-1]
上述矩阵的两个数组为:
代码实现:
//快速转置
template<class T>
SparseMatrix<T> SparseMatrix<T>::FastTransport()
{
assert(_a.size() < 0);
SparseMatrix<T> result;
//行列size互换
result._rowSize = _colSize;
result._colSize = _rowSize;
result._invalid = _invalid;
//建立rowCounts和rowStart
int* rowCounts = new int[_colSize];
int* rowStart = new int[_colSize];
memset(rowCounts, 0, sizeof(int)*_colSize);//初始化为0
memset(rowStart, 0, sizeof(int)*_colSize);//初始化为0
result._a.resize(_a.size());//复制顺序表_a,容量相同,但是数据不同。
//初始化
for (size_t i = 0; i < _colSize; i++)
{
rowCounts[_a[i]._col]++;
}
rowStart[0] = 0;
for (size_t i = 1; i < _colSize; i++)
{
rowStart[i] = rowCounts[i - 1] + rowStart[i - 1];
}
//快速转置
size_t index = 0;
Triple<T> tmp;
while (index < _a.size())
{
int row = _a[index]._col;//行数
int rowIndex = rowStart[row];//当前行的起始位置
//交换行和列
tmp._value = _a[index]._value;
tmp._row = _a[index]._col;
tmp._col = _a[index]._row;
result._a[rowIndex] = tmp;
rowStart[row]++;
index++;
}
delete[] rowCounts;
delete[] rowStart;
return result;
}算法分析:
一次定位快速转置算法时间主要浪费在3个并列的循环中,分别执行了_colSize,_col_Size,_a.size()次,总的时间复杂度为O(_colSize+_a.size())。远远小于O(_colSize*_a.size)。









![Image [2].png wKiom1cTnn_SDYj9AAAczW2rlyw473.png](http://s3.51cto.com/wyfs02/M00/7F/1B/wKiom1cTnn_SDYj9AAAczW2rlyw473.png)














 121
121

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








