KDY-C++-CSP-二轮模拟题（2）-----ZHX补题报告

1.比赛情况

T1 下棋	T2 汪洋	T3 删数	T4 平分糖果	总分
100pts(AC)	0pts(WA)	0pts(NP)	90pts(TLE)	190

                                赛后AK

2.赛中概况

第一题难度跟昨天差不多，用的是结构体排序，15分钟就A了，比较顺利。

然后做的第四题，第四题开始没大仔细读，编完后调试调出了十几个bug，改完之后又发现思路不对，又重新写（其实没啥难度，主要是思维），然后耗时30分钟左右编完（蒟蒻的自己）。

第二题也是非常的 水 ，我用的dfs 写了一大串最后只能输出0。正解是用前缀和做的，代码挺容易理解的。第三题直接没思路，没怎么做。

3.题目分析

T1 下棋

赛中情况：AC

1.1 问题描述

Meowowco 最近沉迷下棋。

众所周知，棋盘上一局有 𝑛n 个玩家一起游戏。

我们的棋子称为”英雄”，英雄分为11、22、33星。11 个 33 星英雄可以由 33 个 22 星英雄合成，11 个 22 星英雄可以由 33 个 11 星英雄合成。

现在给出每名玩家的英雄阵容，我们定义阵容强度为 18𝑥+3𝑦+𝑧18x+3y+z，其中 𝑥x 为 33 星英雄个数，𝑦y 为两星英雄个数，𝑧z 为一星英雄个数，其中可以用低星英雄合成高星英雄后再计算阵容强度。

根据玩家的阵容强度，将玩家序号进行排序，并按阵容强度从大到小的顺序输出玩家的序号（若阵容强度相同，则把玩家序号（第𝑖i个输入的玩家序号为𝑖i）小的排在前面）。

1.2 输入格式

从文件chess.in中读取数据。

第一行输入一个整数 𝑛n (1≤𝑛≤1000001≤n≤100000)，表示有𝑛n名玩家参加游戏。

接下来𝑛n行，每行包含三个整数，代表玩家 𝑖i 的一星、二星、三星英雄的数量。

1.3 输出格式

输出到文件chess.out中。

将玩家序号进行排序，并按阵容强度顺序输出玩家的序号（若阵容强度相同，则按玩家序号排序）。

1.4 输入样例1

9

2 3 1

1 3 3

0 0 4

1 4 3

4 1 4

1 4 1

0 1 4

0 1 4

2 3 2

1.5 输出样例1

5 4 7 8 2 3 9 6 1

1.6 输入样例2

2

1 2 0

1 2 2

1.7 输出样例2

2 1

1.8 数据描述

保证所有数据点均满足 1≤𝑛≤105​​，0≤𝑥,𝑦,𝑧≤109​​。

分析

求出转化后的阵容强度和序号即可（三年OI一场空，不开long long见祖宗）

AC码 ：

#include<bits/stdc++.h>
using namespace std;
const int N=500500;
struct qq{
	long long x,y,z;
	long long id,sum;
}a[N];
bool cmp(qq f,qq l){
	if(f.sum!=l.sum){
		return f.sum>l.sum;
	}else{
		return f.id<l.id;
	}
}
int main(){
	freopen("chess.in","r",stdin);
	freopen("chess.out","w",stdout);
	long long n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i].z>>a[i].y>>a[i].x;
		if(a[i].z>=3){
			a[i].y+=(a[i].z/3);
			a[i].z%=3;
		}if(a[i].y>=3){
			a[i].x+=(a[i].y/3);
			a[i].y%=3;
		}a[i].id=i;
		a[i].sum=a[i].x*18+a[i].y*3+a[i].z*1;
	}sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++){
		cout<<a[i].id<<" ";
	}
	return 0;
}

T2 汪洋

2.1 问题描述

Meowowco 连夜坐飞机去参加上海国家会展中心的 BilibiliWorld 2023，可是到现场时，已经是一片汪洋。。。

就算是这样，Meowowco 也不算白来一趟，因为场馆里还有许多可爱的 coser，她可以和这些 coser 一起合影，然后发说说羡慕她那可怜的队友。

场馆可以看成一张由 n×nn×n 个格子构成的矩阵。场馆内的格子可能被水淹没，Meowowco 趟水走过去可能会影响心情，因此这些格子上的值为 负数。但是另外的一些格子上站着可爱的 coser，如果 Meowowco 可以与那些 coser 合影，那么她就会变得开心，因此这些格子的值为 正数。

Meowowco 最开始的心情为 100100 点，她在逛 BW 的过程中：

如果走到值为正数的格子，说明可以和可爱的 coser 拍照，因此会增加心情。

如果走到值为负数的格子，说明 Meowowco 需要趟水，因此心情值会下降。

Meowowco 从 (1,1)(1,1) 点向右出发，即朝 (1,2)(1,2) 点出发，她每次移动只能移动到 一个相邻的格子，并且她需要按照下面的路线逛一圈：

沿着上一步的方向继续移动

进行顺时针 9090 度转向，(注意不可以在同一个格子内连续转向)

不再逛那些逛过的格子（除了起点）

其中转向指的是：如果上一步向右走，那么转向之后则为向下走；如果上一步向左走，那么转向之后则为向上走……

那么逛完 BW 之后，肯定是要从 (1,1)(1,1) 点离开然后回家的，那么问题来了，Meowowco 离开时心情值最大是多少。

2.2 输入格式

从文件BigWater.in中读取数据。

第一行输入一个整数 nn，表示地图的大小。

第二到 N+1N+1 行，每行包含 nn 个整数 aija​ij​​，表示每个格子的值。

保证 (1,1)(1,1) 点为 00。

2.3 输出格式

输出到文件BigWater.out中。

输出一个整数，表示 Meowowco 最大的心情值。

2.4 输入样例1

1. 5
2. 0 -3 8 -2 3
3. 3 -1 -3 -10 -6
4. 9 -9 -6 10 -7
5. -2 -4 -9 6 -10
6. -1 8 -7 10 -5

2.5 输出样例1

1. 129

2.6 输入样例2

1. 5
2. 0 5 2 2 -7
3. 10 7 -5 7 1
4. 4 -1 -5 4 -6
5. 3 -2 3 4 0
6. -6 -1 -8 9 -6

2.7 输出样例2

1. 142

2.8 数据描述

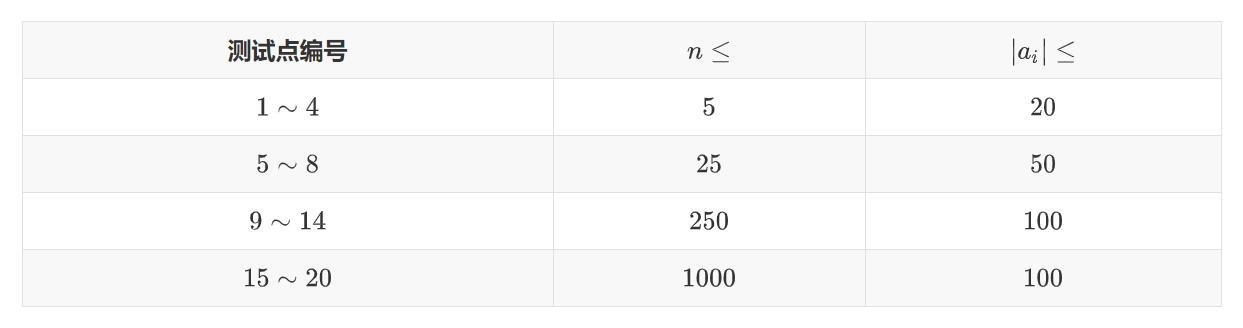
保证所有数据点均满足 1≤n≤1031≤n≤10​3​​，∣ai∣≤100∣a​i​​∣≤100。

分析：

利用前缀和的方法，在输入过程中 把地图分成一个个矩形，计算矩形内的数字总和（sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]）。分别枚举轮廓上的数字总和（sum[i][j]-sum[i-1][j-1]+sum[1][j]+sum[i][1]-sum[1][1]-a[1][j]-a[i][1]），选出最大值。

AC码:

#include<bits/stdc++.h>
using namespace std;
int sum[1019][1045]={0},a[1045][1019];
int main(){
	
	int n,maxx=0;
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			cin>>a[i][j];
			sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];
		}
	}for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			maxx=max(maxx,sum[i][j]-sum[i-1][j-1]+sum[1][j]+sum[i][1]-sum[1][1]-a[1][j]-a[i][1]);
		}
	}cout<<100+maxx;
	return 0;
} 

T3 删数

赛中情况  WA 0pts

3.1 问题描述

有一个集合，初始状态里面有数字 11、22、33、44、55、……、1145141919810114514​1919810​​，你可以理解为很多正整数。

现在给你一个长度为 nn 数组 a(1≤ai≤109)a(1≤a​i​​≤10​9​​)，每次操作将当前集合中第 a1a​1​​ 小、第 a2a​2​​ 小、……、第 ana​n​​ 小的数同时移除。

现在有 qq 次询问，每次询问包含一个整数 xx，查询从初始状态到删除 xx 需要操作多少次。若无法删除，输出 0。

3.2 输入格式

从文件delnum.in中读取数据。

第一行包含两个正整数 n(1≤n≤105)n(1≤n≤10​5​​)，表示数组大小。

接下来一行包含 nn 个正整数 a1a​1​​，a2a​2​​，……，ana​n​​，含义如题目描述所述。

接下来一行包含一个正整数 qq，表示查询次数。

接下来 qq 行，每行包含一个正整数 xx。

数据保证 a1<a2<.....<an≤109a​1​​<a​2​​<.....<a​n​​≤10​9​​

3.3 输出格式

输出到文件delnum.out中。

对于每次询问，输出占一行，包含一个整数，表示删除 xx 需要操作多少次。若无法删除，输出 0。

3.4 输入样例

1. 5
2. 1 2 3 4 5
3. 1
4. 100

3.5 输出样例

1. 20

3.6 输入样例

1. 5
2. 1 3 9 14 20
3. 5
4. 114
5. 514
6. 1919
7. 810
8. 233

3.7 输出样例

1. 27
2. 107
3. 388
4. 159
5. 45

3.8 数据描述

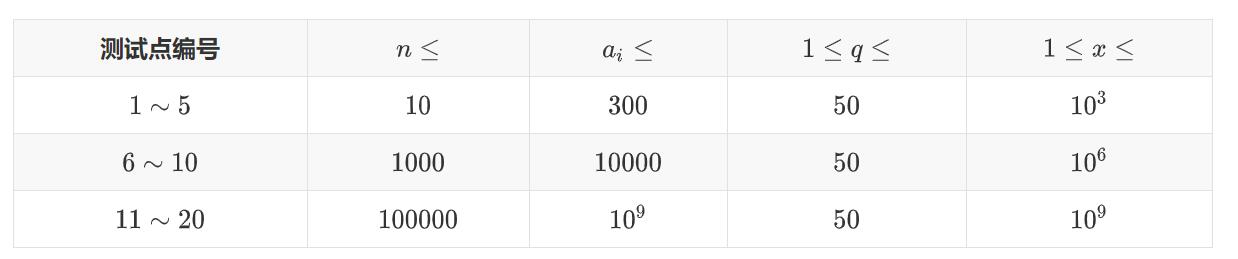
保证所有数据点均满足 1≤n≤1051≤n≤10​5​​，1≤ai≤1091≤a​i​​≤10​9​​，1≤q≤501≤q≤50，1≤x≤1091≤x≤10​9​​。

 简单分析 ：

   简简单单     思维题。

找找规律就能A。

AC码：

#include<bits/stdc++.h>
using namespace std;
int n,q,a[114514],x;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}cin>>q;
	while(q--){
		cin>>x;
		int sum=0,f=0,ans=0;
		for(int i=n;i>0;i--){
			if(a[i]<=x){
				ans+=(x-a[i])/i;
				x=a[i]+(x-a[i])%i;
				if(x>a[i]){
					x-=i;
					ans++;
				}
			}if(x==a[i]){
				cout<<ans+1<<endl;
				f=1;
				break;
			}
		}if(!f)cout<<"0\n";
	}
	return 0;
} 

 T4 平分糖果

4.1 问题描述

小可的妈妈给了小可很多的糖果，已经糖果都有美味程度，美味程度用1~6的整数表示。

有一天达达来小可家做客，小可要把糖果分给达达，现在已知了美味程度为 i 的糖果有 a[i] 个，请问小可能不能把糖果平分成美味程度之和相同的两部分。

4.2 输入格式

多组输入，每行输入6个数字，表示美味程度为 i 的糖果有 a[i] 个。

以输入一行6个0作为终止条件。

4.3 输出格式

对于每组输入，第一行输出为： Collection #k: ，k为第几组输入。

第二行输出为：如果可以平均分，则输出Can be divided.，否则输出Can't be divided. 。

4.4 输入样例

1. 1 0 1 2 0 0
2. 1 0 0 0 1 1
3. 0 0 0 0 0 0

4.5 输出样例

1. Collection #1:
2. Can't be divided.
4. Collection #2:
5. Can be divided.

4.6 数据描述

20%的数据：糖果总数不超过100

100%的数据：糖果总数不超过 20000

分析：

确定平分a[1]的值求2，3，4，5，6。满足==t表示能平分。

于是就有了：

#include<bits/stdc++.h>
using namespace std;
const int N=100500;
int main(){
	freopen("candy.in","r",stdin);
	freopen("candy.out","w",stdout);
	int p=0;
	while(++p){
		int a[11];
		int sum=0,t;
		bool flag=true,fflag=false;
		for(int i=1;i<=6;i++){
			cin>>a[i];
			sum+=(a[i]*i);
			if(a[i]!=0)flag=false;
		}if(flag==true)break;
		cout<<"Collection #"<<p<<":"<<endl;
		if(sum%2)cout<<"Can't be divided.\n\n";
		else{
			t=sum/2;
			for(int i=0;i<=a[1]&&t>=i;i++){
				for(int j=0;j<=a[2]&&t>=2*j+i;j++){
					for(int k=0;k<=a[3]&&t>=3*k+i+j*2;k++){
						for(int l=0;l<=a[4]&&t>=4*l+i+j*2+k*3;l++){
							for(int m=0;m<=a[5]&&t>=5*m+i+j*2+k*3+l*4;m++){
								for(int n=0;n<=a[6]&&t>=n*6+i+j*2+k*3+l*4+m*5;n++){
									if(i+j*2+k*3+l*4+m*5+n*6==t){
										fflag=true;
										break;
									}
								}if(fflag==true)break;
							}if(fflag==true)break;
						}if(fflag==true)break;
					}if(fflag==true)break;
				}if(fflag==true)break;
			}if(fflag==true)cout<<"Can be divided.\n\n";
			else cout<<"Can't be divided.\n\n";
		}
	}
	return 0;
}

    别抄，是错的     

 算下来，时间复杂度约等于O(n^6)!!

但也顺走了90pts。

AC分析：

   煎蛋    的多重背包

二维，一维存a[i],二维存max

AC码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5;
int n,q,x,dp[10][2*N],a[10];
int main(){
	//freopen("candy.in","r",stdin);
	//freopen("candy.out","w",stdout);
	int cnt=0;
	while(++cnt){
		int m=0;
		for(int i=1;i<=6;i++){
			cin>>a[i];
			m+=a[i]*i;
		}if(!m)break;
		dp[0][0]=1;
		for(int i=1;i<=6;i++){
			for(int k=0;k<=a[i];k++){
				for(int j=k*i;j<=m/2+1;j++){
					dp[i][j]=dp[i][j] | dp[i-1][j-k*i];
				}
			}
		}cout<<"Collection #"<<cnt<<":\n";
		if(m%2==0&&dp[6][m/2]==1)cout<<"Can be divided.\n\n";
		else cout<<"Can't be divided.\n\n";
	}
	return 0;
}

AKIOI