强化学习医学案例——脓毒症人工智能治疗决策

脓毒症是全世界第三大死因，也是医院1-3级死亡的主要原因，但是最好的治疗方法。战略仍然不确定。特别是，有证据表明目前静脉输液的做法而血管加压剂是次优的，在1,4-6比例的患者中可能会引起伤害。解决这个连续的决策问题，我们开发了一种强化学习剂，人工智能临床医师，它提取了内隐从大量患者数据中获得的知识，超过了临床医生的生活经验的许多倍通过分析大量（大部分是次优的）治疗决定来优化治疗。我们证明了人工智能临床医师选择的治疗平均可靠，且高于人类临床医师。在一个独立的大型验证队列中，临床医师实际剂量与人工智能决定相匹配的患者死亡率最低。我们的模型为脓毒症提供个性化和临床可解释的治疗决策，可以改善患者的预后。

脓毒症是指严重感染导致危及生命的急性器官功能障碍。脓毒症患者静脉输液和血管加压剂的管理是一项关键的临床挑战，也是一项重要的研究重点。除了一般的指导方针，如“幸存的脓毒症运动”，目前还没有工具来个性化治疗脓毒症，并协助临床医生在实时和患者层面做出决定。因此，脓毒症治疗的临床变异性是极端的，一致的证据表明，不理想的决定导致较差的结果。

我们开发了人工智能临床医师，一个使用强化学习的计算模型，它能够动态地为重症监护室（ICU）的成年脓毒症患者提供最佳治疗建议。强化学习是一类人工智能工具，其中虚拟代理从试验和错误中学习一组优化的规则——一种最大化预期回报的策略。同样，临床医生的目标是做出治疗决定，以最大限度地提高患者获得良好结果的可能性。强化学习具有许多有益于医学决策的特性。利用强化学习的模型的内在设计可以处理稀疏的奖励信号，这使得它们非常适合于克服与患者对医疗干预反应的异质性和治疗效果的延迟适应症相关的复杂性。重要的是，这些算法能够从次优训练示例中推断出最优决策。强化学习在过去已经成功地应用于医疗问题，如糖尿病和重症监护室的机械通气。

人工智能临床医师建立在两个不重叠的大型重症监护室数据库上，该数据库包含从美国成人患者常规收集的数据。重症监护医疗信息集市第三版（MIMIC-III）用于模型开发，EICU研究所数据库（ERI）用于模型测试。在这两个数据集中，我们包括符合国际共识的脓毒症3标准的成年患者。排除不合格病例后，我们分别从一所三级教学医院的5个独立ICU中纳入17083例（88.4%符合条件的脓毒症患者），从128所不同医院中纳入79073例（73.6%符合条件的脓毒症患者），这些医院分别来自Mimic-III ERI（SUP初步图1）。患者人口统计和临床特征见表1和补充表1。

在这两个数据集中，我们提取了一组48个变量，包括人口统计学、艾力克斯豪斯预吸收状态、生命体征、实验室值、收到的液体和血管加压剂（补充表2）。患者的数据被编码为具有4小时时间步骤的多维离散时间序列，对于每个患者，我们包括在估计的脓毒症发作时间周围进行的72小时测量。每4小时内静脉输液总量和最大剂量的血管加压剂定义了感兴趣的药物治疗。该模型旨在优化患者死亡率，因此奖励与生存率和死亡惩罚相关。

采用马尔可夫决策过程（MDP）对患者环境和轨迹进行建模。模型的各个元素是使用来自训练集的患者数据时间序列定义的（模拟-III的80%随机样本；图1）。我们部署了人工智能临床医师来解决MDP并预测治疗策略的结果。首先，我们通过分析所有处方并计算每个治疗方案的平均回报率来评估临床医师的实际治疗，在我们的模型中，每个治疗方案的平均回报率可以取-100到+100的值。然后，使用策略迭代法求解MDP，确定最大回报的治疗，即模拟III组患者的预期90-D生存率。以下简称“人工智能政策”。

                           

使用另一项策略（临床医师策略）产生的患者轨迹评估新人工智能政策的绩效被称为策略外评估。在不部署新策略的情况下获得可靠的绩效评估至关重要，因为执行糟糕的策略会对患者造成危险。因此，我们实施了一种高置信度政策评估（hcope）方法（加权重要性抽样（wis）），并使用自举估计法来估计Mimic-III 20%验证集（图2b和补充图1）中政策值的真实分布。我们使用500种不同的训练数据聚类解决方案建立了500种不同的模型，选择的最终模型最大化了人工智能策略的95%置信下限。图2a表明，如果建立了足够的模型，这个界限始终超过临床医师政策的95%置信上限。该模型选择方法最大限度地提高了新人工智能策略的理论统计安全性。然后在独立的ERI数据集上测试所选的人工智能策略。通过绘制临床医师政策的回归与患者90天死亡率之间的关系（图2c），证实了良好的模型校准。在图2d中，我们显示了幸存者和非幸存者的平均回报。

图2最佳人工智能策略和模型校准的选择。A，在构建500个模型期间，最佳人工智能策略的95%下限（lb）和最高价值临床医师策略的95%上限（ub）的演变。在仅有几个模型之后，在可接受的风险范围内，人工智能策略的价值高于临床医生的治疗。n=13666名患者在Mimic-III开发数据集中，n=3417名患者在Mimic-III测试集中，n=79073名患者在ERI测试集中。b.模拟III试验组中500个模型（每个箱线图中n=500个模型）临床医生实际治疗的估计值、人工智能策略、随机策略和零药物策略的分布。选择的人工智能策略最大化95%的置信下限。c，模拟III训练组（n=13666例）临床医师治疗的恢复与患者90-D死亡率之间的关系。行动的返回被分为100个分桶，并计算每个分桶中观察到的平均死亡率（原始的蓝线，平滑的红线）。蓝色阴影区域代表低回报的S.E.M.治疗与高死亡率相关，而高回报治疗导致更好的生存率。d，模拟三训练集中幸存者（n=11031）和非幸存者（n=2635）的平均回报率。C和D由2000次重新采样的训练数据中的引导生成。

 

图3a显示了临床医师政策和人工智能政策的估计值在ERI队列中所选最终模型中的分布。使用2000次重新取样的引导法，临床医师策略和人工智能策略的中值分别估计为56.9（四分位距，54.7–58.8）和84.5（四分位距，84.3–87.7）。

图3b，c表示根据和临床医生人工智能政策的治疗剂量分布。平均而言，人工智能临床医师建议比临床医师的实际治疗有较低的剂量的静脉输液和较高剂量的血管加压剂。ERI患者接受血管加压药物的时间比例仅为17%，但如果遵循人工智能临床医师的建议，这一比例将达到30%。我们通过分析实际给药剂量与人工智能临床医师建议的剂量一致或不同时的患者死亡率进一步验证了该模型。58%的时间，患者在0.02μg/kg体重/min（μg/kg/min）或10%（以较小者为准）的范围内接受非常接近建议剂量的血管加压剂。对于液体，患者接受建议剂量约36%的时间，在10毫升/小时或10%之内。这些患者接受的剂量与人工智能临床医生推荐的剂量相似，死亡率最低。当实际给药剂量与建议剂量不同时，临床医生会以相同比例给药，并减少75%的加压时间。两种治疗中的一种比人工策略多或少的治疗与剂量依赖性的死亡率增加相关。图3d，e描述了与患者水平的平均剂量间隙的关联。接受太少血管加压剂的患者的中位剂量不足为0.13μg/kg/min（四分位间距，0.04–0.27μg/kg/min）。

使用随机森林分类模型，我们通过估计模型参数对预测两种药物的使用的相对重要性，对模型表示和可解释性有了一些了解（补充图2）。这证实了人工智能临床医师提出的决定是临床上可解释的，主要依赖于合理的临床和生物学参数。在这里，我们演示了强化学习如何应用于解决复杂的医学问题，并提出了针对脓毒症的个性化和临床可解释的治疗策略。在一个独立的队列中，接受人工智能临床医师建议的治疗的患者死亡率最低。

当临床医生的实际治疗与人工智能临床医生的建议政策不同时，是最常见的给药太少的血管加压剂。早期使用低剂量的血管加压剂可能在脓毒症中起作用；这可能会避免摄入过量的液体，这与不良结果有关。我们的结果支持这一策略，但重要的是允许对每个患者进行个性化治疗。我们设想这个系统将被实时使用，从不同的数据流中获得的患者数据被输入到与我们的算法相匹配的电子健康记录软件中，这将建议采取行动。医生总是需要对治疗策略作出主观的临床判断，但是计算模型可以提供关于最佳决策的额外见解，避免以短期复苏目标为目标，而是遵循长期生存的轨迹。我们开发的强化学习方法对所用数据不可知，原则上可以应用于任何数据丰富的临床环境和许多医疗干预。在未来，很可能随着“OMIC”技术的发展，这些附加信息将被添加到人工智能临床医师中，以改进状态定义并指导选定患者组的更多治疗。

然而，我们的研究也有局限性。尽管我们使用的数据集很大，包括常规收集的临床数据，但由于数据记录质量差或数据丢失，一些站点和患者必须排除在外。由于两个数据集之间的差异，使用了略有不同的脓毒症3标准实施，并在ERI中使用了医院死亡率而不是90-D死亡率。显然，这项工作需要在临床试验中使用实时数据和决策进行前瞻性评估，并在不同的医疗环境中进行测试，但脓毒症死亡率仅降低一小部分，将代表每年挽救数万条生命。世界在过去的10-15年里，试图开发新的治疗方法来降低脓毒症死亡率的尝试都没有成功。因此，使用计算机决策支持系统更好地指导治疗和改善结果是一种非常需要的方法。

 

ICU论文要点

1、数据分布及处理

     从这两个数据集中，我们提取了一组48个变量，包括人口统计学、艾力克斯豪斯预吸收状态、生命体征、实验室值、接受的液体和血管加压剂以及液体平衡（补充表2）。

       对患者的数据进行编码。作为具有4小时时间步长的多维离散时间序列。在4小时时间步内多次测量的数据变量被取平均值（例如心率）或总和（例如尿量）。使用频率直方图方法和单变量统计方法（Tukey方法）检查所有特征的异常值和误差。在可能的情况下纠正了错误（例如，将温度从华氏度转换为摄氏度）。

       缺失值最近邻插补法插补

2、建立计算模型。

     疾病过程可以被表述为部分可观察的MDP。使用MDP来近似患者的轨迹并模拟决策过程。MDP由元组s、a、t、r、γ定义，其中：

T（S′，S，A），过渡矩阵，包含action A使得状态S在时间T+1时变为状态S’的概率，描述了系统的动力学。

状态空间是由病人数据的k-means++聚类构建的，从而产生750个相互排斥的病人状态。我们使用贝叶斯和阿卡克信息准则来确定最佳簇数（补充图3e）。我们选择了高值k来确保高粒度模型，同时避免使用过大的状态空间（>1000），这将导致非常稀疏的状态（补充图3a）。两种吸收状态被添加到状态空间，对应于患者的死亡和出院。为了进一步评估我们国家汇总的有效性，我们使用了国际疾病分类代码在各国的分布，并证明过去的病史和诊断在一定程度上被封装在我们选定的国家定义中（补充图3b）。

在进行聚类之前，考虑到数据的均值和方差不相等，对正态分布数据进行了标准化，对对数正态分布变量进行了标准化之前的对数变换，并将二进制数据集中在零上。采用分位数-分位数图和频率直方图等可视化方法对各变量的正态性进行检验。

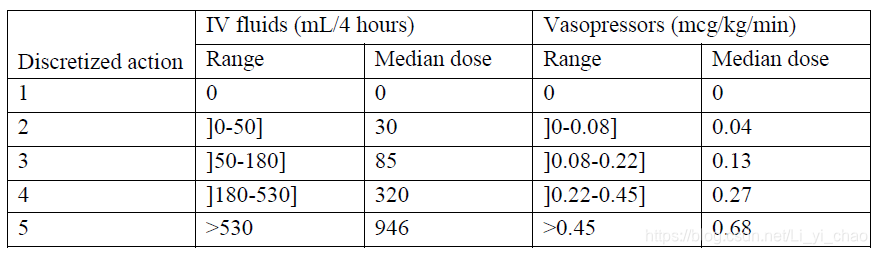
一个关键的挑战是静脉输液和血管加压剂的管理。因此，我们将重点放在每4小时内静脉输液总量和最大血管加压剂剂量的医疗决策上。静脉输液包括滴注和背景下的晶体、胶体和血液制品，如前所述，这些都是按张力标准化的。血管加压素包括去甲肾上腺素、肾上腺素、血管加压素、多巴胺和苯肾上腺素，必要时使用先前公布的剂量对应物37将其转化为去甲肾上腺素当量。为了确定作用空间，每种治疗的剂量被表示为五种可能的选择之一，选择1是“不给药”，剩余的非无效剂量被分为四个四分位数（补充表3）。两种治疗方法的结合产生了25种可能的离散作用。我们将建议剂量表示为与建议作用相匹配的每个剂量箱的中位数。

A：将750个健康状态映射到低维投影。每个点代表一个簇形心，其大小和颜色分别对应于该记录的数量和平均死亡率。PC：主要成分。在死亡率中可以看到自发梯度。这表明状态成员确实与死亡率有关。

B.以100个最常用的国际疾病分类（ICD）代码作为替代，获取模型的临床概念和既往病史。我们测量了在所有状态下有多少患者具有给定的ICD代码，并显示了患者状态之间的累积和，从具有给定代码的患者数量最多的状态开始。黑色虚线显示了各州患者的累计总数，各州按降序排列。这是我们应该得到的理论分布，如果ICD代码被随机分配到集群（给定ICD代码的比例在所有状态都应该是全局相等的）。与随机分布的代码相比，大多数患者的状态较少。例如，ICD编码为“天然冠状动脉冠状动脉粥样硬化”的患者中有50%只在23个州发现。如果代码在美国随机分布，这个数字将是79。

C-D，马尔可夫性质的验证。我们在500次试验中，通过观察一种药剂在遵循过渡矩阵时在给定状态下保持多长时间，来测量每种状态下的预期寿命。以一种状态下的预期寿命为例，具有拟合的指数衰减函数。在本例中，数据与拟合函数之间的相关系数r2为0.99。d，模型750个状态下预期寿命与指数衰减函数相关系数的分布。高中位数相关系数0.97（四分位间距0.1）证实大多数州的预期寿命确实是无记忆的。

e.选择模型中的簇数。贝叶斯信息准则（BIC）、阿卡克信息准则（AIC）和簇内平方和是簇数的函数。AIC的最小值为2000左右，BIC的最小值为400。

 

连续状态和动作的序列称为患者的轨迹。在我们的模型中，我们使用医院死亡率或90-D死亡率作为系统定义的惩罚和奖励的唯一定义因素。当一个病人存活下来时，在每个病人的轨迹末端释放一个正的奖励（一个+100的“奖励”）；如果病人死亡，则释放一个负的奖励（一个-100的“惩罚”）。

我们通过计算在模拟III训练数据集中观察到的每个转换的次数并将转换计数转换为可能的矩阵来估计转换矩阵t（s′，s，a）。在高风险环境中（执行错误的策略可能导致危害），将操作空间限制为已知选项是提高模型安全性的明智选择。我们限制了从临床医生经常观察到的动作中选择的一组动作，排除了少于5次的转变。因此，由此产生的人工智能策略建议临床医生在所有选择（相对频繁）中最好的治疗方法。

马尔可夫模型依赖马尔可夫性质，即转换（给定状态和动作）是无记忆的。在马尔可夫链中离开状态的概率保持不变，不管代理处于状态多长时间。因此，保持状态的概率遵循指数衰减38。我们测量了每个状态的经验状态持久性概率，发现数据与几乎所有状态的指数衰减分布之间具有很高的拟合优度（补充图3）。

衰减因子γ定义了强化学习代理的范围，即与当前状态下的奖励相比，对未来奖励的重要性。它可以取0到1之间的值。我们选择的γ值为0.99，这意味着我们对晚期死亡的重视程度几乎与早期死亡的重视程度相当。

 

###欢迎加入全网音频视频课程共享群群，和各领域大佬一起讨论学习知识####

（若群二维码过期，可先加个人微信再拉进群）