LC振荡器电路原理分析

Lincoln_Space

已于 2023-05-30 16:17:30 修改

阅读量8.6k

点赞数 7

文章标签：学习方法硬件工程

于 2023-05-30 15:57:47 首次发布

本文链接：https://blog.csdn.net/Lincoln_Space/article/details/130918271

版权

链接1：高频课程设计_LC振荡器_克拉泼 - 百度文库 (baidu.com)

链接3：https://www.cnblogs.com/xiaobaibai2021/p/15716934.html

模拟电路-p417~418

链接4：山东大学高频电子线路实验三正弦波振荡器实验详解-腾讯云开发者社区-腾讯云

正弦波振荡器背景：

概述

正弦波振荡电路是在没有外加输入信号的情况下，依靠电路自激振荡而产生正弦波输出电压的电路。广泛地应用于两侧、遥控、通讯、自动控制、热处理和超声波电焊等加工设备之中，也作为模拟电子电路的测试信号。下面介绍一下LC正弦波振荡电路的工作原理，并通过multisim软件进行仿真验证。

LC正弦波振荡电路的工作原理

正弦波振荡电路需由以下四个部分组成：

放大电路：保证电路能够有从起振到动态平衡的过程，使电路获得一定幅值的输出量，实现能量的控制；
选频网络：确定电路的振荡频率，使电路产生单一频率的振荡，即确保电路产生正弦波振荡。
正反馈网络：引入正反馈，使放大电路的输入信号等于反馈信号；
稳幅环节：也就是非线性环节，作用是使输出信号幅值稳定。

一般以1MHz振荡频率为界，低于1MHz的振荡频率，使用RC正弦波振荡电路，高于1MHz的振荡频率，使用LC正弦波振荡电路：

图1 LC选频电路

信号频率较低时，电容阻抗很大，网络呈感性；信号频率较高时，电感的感性很大，网络呈容性；当f=f0时，网络呈纯阻性，且阻抗无穷大。此时电路产生谐振，相位差为0。

电路导纳：

$Y=\frac{R}{R^{2}+(\omega L)^{2}} + j\left [ \omega C-\frac{\omega L}{R^{2}+(\omega L)^{2}} \right ]$

虚部为0， $Q=\frac{\omega_{0 }L}{R}\gg 1$ 时：

$\omega _{0}\approx \frac{1}{\sqrt{LC}}$

电容反馈式振荡电路

也称之为电容三点式电路。将晶体管的三个电极，分别与三个电抗性原件相连接，形成三个接点。

图2 电容三点式电路

当LC电路的Q值远大于1时:

$f_{0}\approx \frac{1}{2\pi \sqrt{LC_{x}}}$

其中Cx为C1与C2的并联电容。反馈系数：

$\left | \dot{F} \right |=\left | \frac{\dot{U_{f}}}{\dot{U_{0}}} \right |\approx \frac{C_{1}}{C_{2}}$

电压放大倍数：

$\left | \dot{A_{u}} \right |=\left | \frac{\dot{U_{0}}}{\dot{U_{i}}} \right |= \beta \frac{{R}'_{L}}{r_{be}}$

其中：

${R}'_{L}= R_{c}\parallel \frac{R_{i}}{\left | \dot{F} \right |^{2}}$

反馈系数与C1/C2成正比，增大C1/C2，则反馈系数增大，利于电路起振，但是会使R‘L减小，不利于起振。

图3 电容三点式电路仿真图

调节C2值，观察起振速度、幅值及频率。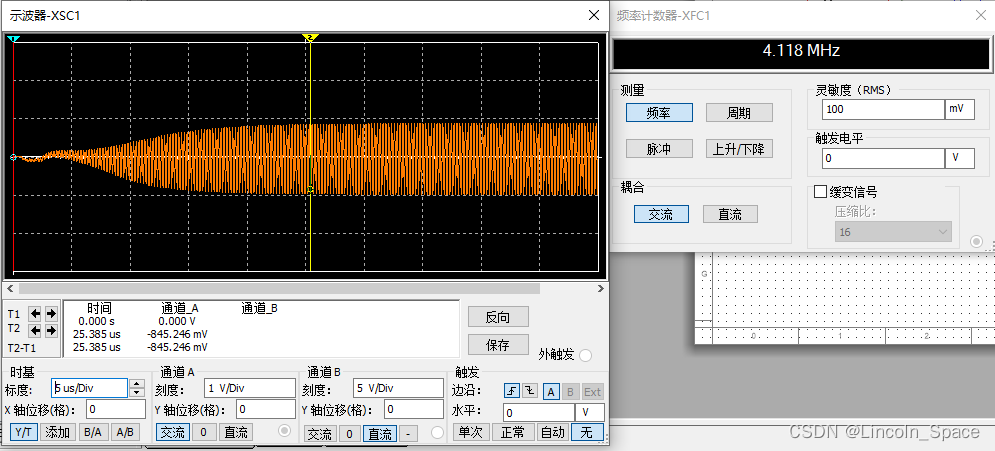

图4 C2为0.2nF时，起振频率为4.12MHz，幅值为0.8V

图5 C2为0.4nF时，起振频率为3.36MHz，幅值为1.46V

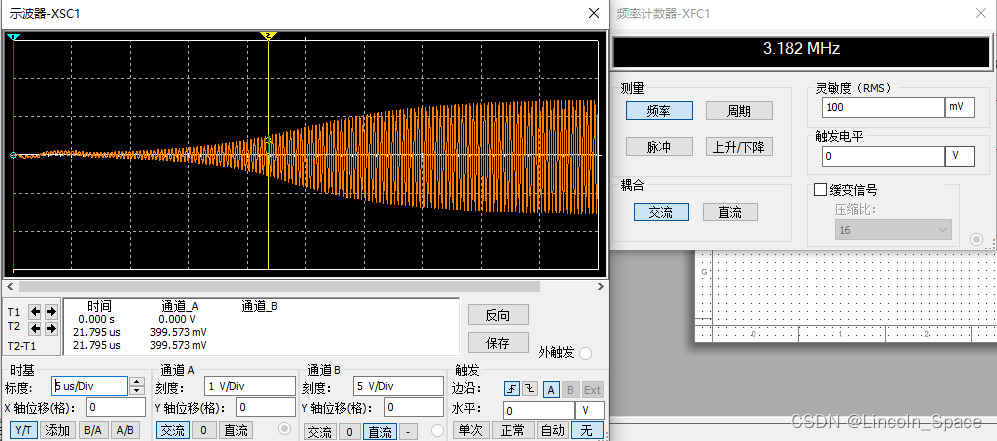
图6 C2为0.5nF时，起振频率为3.18MHz，幅值为1.46V

为了调节f0，需减小C1、C2和L值，但是减小到一定程度，晶体管结间电容将影响振荡频率。因此可以在L所在之路串联一个小的电容C，且C<<C1，C2。总电容≈C，电路振荡频率：

$f_{0}\approx \frac{1}{2\pi \sqrt{LC_{}}}$

振荡频率与C1、C2无关，也几乎与结间电容和杂散电容无关。电路图如下：

图7 改进型克拉波电路

即为改进型克拉波电路。该电路反馈系数取决于C1与C2的比值，谐振频率取决于C与L。因此，改变振荡频率可不影响反馈系数，振荡幅值比较稳定，但是C不能太小，否则会导致停振。

图7 改进型克拉波电路仿真图

石英晶体谐振器

链接4：串/并联谐振电路的仿真分析-电子发烧友网

石英晶振具有非常稳定的固有频率。对于振荡频率的稳定性要求高的电路，应选用石英晶体作为选频网络。

石英晶体等效电路见下图。不振动时，等效为一个平板电容C0，称为静态电容。晶体内部振动时，机械振动的惯性等效为电感L，晶体由于压电效应带来的厚度变化带等效为电容Cs，晶体振动会产生热损耗等效为电阻R。

支路阻抗：

$Z=R+j\left ( \omega L-\frac{1}{\omega C} \right )$

$\left | Z \right |=\sqrt{R^{2}+\left ( \omega L-\frac{1}{\omega C} \right )^{2}}$

当等效电路中L、R、C支路产生串联谐振时，该支路呈纯阻性，等效电阻为R，谐振频率：

$fs=\frac{1}{2\pi \sqrt{LC}}$

整个网络的电抗等于R并联C0的容抗，因R<<wC0，因此近似认为石英晶体呈纯阻性，等效电阻为R。

当f<fs时，C0与C电抗较大，石英晶体呈现容性。

当f=fs时，C0电抗较小，石英晶体呈现纯阻性。

当fs<f<fp时，支路呈感性，石英晶体呈现感性。

当f=fp时，支路呈感性上升，与C0产生并联谐振，石英晶体呈现纯阻性，谐振频率：

$fp=\frac{1}{2\pi \sqrt{L\frac{CC0}{C+C0}}}=fs\sqrt{1+\frac{C}{C0}}$

其中C0远大于C，因此fp≈fs。

当f＞fp时，电抗主要取决于C0，石英晶体呈容性。

图8 石英晶振的等效电路图HC-49/U_5MHz对应的Rs\Cs\Ls\C0参数

图9 等效电路图（上）及晶振电路（下）阻抗分析

根据石英晶体的特性，因此石英晶体可以工作在两种状态，一种为串联谐振，石英晶体工作在fs附近，表现为纯阻态；一种为并联谐振，石英晶体工作在fp附近，表现为电感。

并联谐振电路

图10 并联谐振

LC振荡电路图11 振荡结果

总结

本文使用multisim分析了LC振荡器三点电容式振荡电路及优化后的电容式振荡电路，分析了通过改变电容调节反馈系数进而实现调频的结果。同时，简单介绍了石英晶振的工作原理，并使用仿真了石英晶振的并联谐振电路。在仿真过程中发现即使按照书本进行参数设置也不容易起振：1.可以增加一个开关，开关启动瞬间会产生一些扰动，产生不同频段的信号，从而起振。2.如果增加开关无法解决，可以试着调节静态工作点来让电路完成起振。