A. Modular Exponentiation

The following problem is well-known: given integers n and m, calculate

,

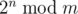where 2n = 2·2·...·2 (n factors), and  denotes the remainder of division of x by y.

You are asked to solve the "reverse" problem. Given integers n and m, calculate

.

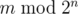Input

The first line contains a single integer n (1 ≤ n ≤ 108).

The second line contains a single integer m (1 ≤ m ≤ 108).

Output

Output a single integer — the value of .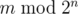

Examples

input

4
42

output

10

input

1
58

output

0

input

98765432
23456789

output

23456789

Note

In the first example, the remainder of division of 42 by 24 = 16 is equal to 10.

In the second example, 58 is divisible by 21 = 2 without remainder, and the answer is 0.

m%2n

2^n太大了，我们是不可能全部算出来的。m范围是固定的，也就是说当n达到一定值时，2^n一定大于m了。所以直接输出m即可。我们就是30，n大于30是，2n就很大了，直接输出m，否则慢慢算