二手车价格预测

目录

前言

题目：

一、数据探索（EDA）

1.读取数据、缺失值可视化

二、数据清洗

三、特征工程

1.构建时间特征

2.匿名特征交叉

 3.平均数编码

四、建模调参

五、模型融合

二、下面这个是另外参考的代码，与上面不同

总结

1、二手车预测价格赛题是一个典型的回归问题，要求参赛者根据给定的数据集预测二手车的零售交易价格。

2、数据集通常包括车辆的基本信息、交易时间信息和价格信息等变量，其中可能包含匿名特征。

3、在比赛中，参赛者需要选择合适的机器学习算法或模型，并进行训练和调优，以提高模型的预测准确性。

4、常用的回归算法包括线性回归、逻辑回归、多项式回归、逐步回归、岭回归、套索回归、弹性网络回归等。

5、此外，参赛者还需要进行数据预处理，包括数据清洗、特征工程、缺失值处理等，以确保数据的质量和可用性。

6、同时，对数据进行探索性分析，如可视化、特征相关性分析等，有助于更好地理解数据和选择合适的模型。

7、最终，模型的预测结果将根据平均绝对误差（MAE）等指标进行评估，MAE 值越小，拟合得越好。

---

前言

赛题属于回归类型，相比于前两次的保险反欺诈及贷款违约预测，本次比赛学到了很多特征工程、模型调参及模型融合的处理，收货颇丰

数据预处理：对数据进行清洗、预处理和特征工程，以确保数据的质量和可用性。这可能包括删除无关列、处理异常值、填充缺失值、进行特征转换等操作。

模型选择与训练：选择适合的机器学习模型，并使用训练集对其进行训练。常见的模型包括决策树、随机森林、神经网络等。

模型评估与调优：使用测试集对训练好的模型进行评估，并根据评估结果对模型进行调优。这可能涉及调整模型的参数、选择合适的特征、进行特征工程等。

预测与提交：使用训练好的模型对测试集进行预测，并将预测结果提交给比赛平台。

在天池比赛中，参赛者可以使用各种机器学习算法和技术，如决策树、随机森林、神经网络等，来构建预测模型。同时，参赛者还需要注意数据的合法性、合理性和异常值处理，以提高模型的准确性和可靠性

题目：

预测二手车的交易价格为任务，该数据来自某交易平台的二手车交易记录，总数据量超过40w，包含31列变量信息，其中15列为匿名变量。为了保证比赛的公平性，将会从中抽取15万条作为训练集，5万条作为测试集A，5万条作为测试集B，同时会对name、model、brand和regionCode等信息进行脱敏。

一、数据探索（EDA）

1.读取数据、缺失值可视化

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
df = pd.read_csv('/train.csv', sep=' ')
# 缺失值可视化
missing = df.isnull().sum()/len(df)
missing = missing[missing > 0]
missing.sort_values(inplace=True) #排个序
missing.plot.bar()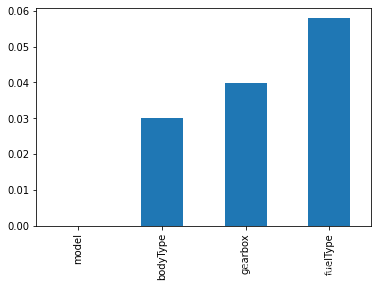

df.describe().T

目标变量price， 75%以下的数据与最大值相差较大，数据呈现一个偏态分布（也可以可视化，会更加直观），这也是后续要进行对数转换的原因。

# 分离数值变量与分类变量
Nu_feature = list(df.select_dtypes(exclude=['object']).columns)  # 数值变量
Ca_feature = list(df.select_dtypes(include=['object']).columns)
plt.figure(figsize=(30,25))
i=1
for col in Nu_feature:
    ax=plt.subplot(6,5,i)
    ax=sns.kdeplot(df[col],color='red')
    ax=sns.kdeplot(test[col],color='cyan')
    ax.set_xlabel(col)
    ax.set_ylabel('Frequency')
    ax=ax.legend(['train','test'])
    i+=1
plt.show()

与目标变量相关性比较高的特征有regDate、kilometer、v_0、v_3、v_8、v_12，这个不难理解，注册日期越早，行驶公里数越多，车价相对会越低。品牌和车型与目标变量的相关性较低这点比较意外。

二、数据清洗

# 众数填充缺失值
df['notRepairedDamage']=df['notRepairedDamage'].replace('-',0.0)
df['fuelType'] = df['fuelType'].fillna(0)
df['gearbox'] = df['gearbox'].fillna(0)
df['bodyType'] = df['bodyType'].fillna(0)
df['model'] = df['model'].fillna(0)
# 截断异常值
df['power'][df['power']>600] = 600
df['power'][df['power']<1] = 1
df['v_13'][df['v_13']>6] = 6
df['v_14'][df['v_14']>4] = 4
# 目标变量进行对数变换服从正态分布
df['price'] = np.log1p(df['price'])

 大部分模型是以数据正态分布为前提，目标变量如果偏态严重，会影响模型预测效果，所以才会进行对数正态化

三、特征工程

特征工程我参考了很多大神的方法，自己也尝试了很多组合在模型上运行，最终确定了这些特征，

毕竟模型都差不多，特征能够对提分有比较显著的效果，更多特征的构建可以参考：

零基础入门数据挖掘系列之「特征工程」-天池技术圈-天池技术讨论区

1.构建时间特征

from datetime import datetime
def date_process(x):
    year = int(str(x)[:4])
    month = int(str(x)[4:6])
    day = int(str(x)[6:8])
    if month < 1:
        month = 1
    date = datetime(year, month, day)
    return date
df['regDate'] = df['regDate'].apply(date_process)
df['creatDate'] = df['creatDate'].apply(date_process)
df['regDate_year'] = df['regDate'].dt.year
df['regDate_month'] = df['regDate'].dt.month
df['regDate_day'] = df['regDate'].dt.day
df['creatDate_year'] = df['creatDate'].dt.year
df['creatDate_month'] = df['creatDate'].dt.month
df['creatDate_day'] = df['creatDate'].dt.day
df['car_age_day'] = (df['creatDate'] - df['regDate']).dt.days#二手车使用天数
df['car_age_year'] = round(df['car_age_day'] / 365, 1)#二手车使用年数

2.匿名特征交叉

num_cols = [0,2,3,6,8,10,12,14]
for index, value in enumerate(num_cols):
    for j in num_cols[index+1:]:
        df['new'+str(value)+'*'+str(j)]=df['v_'+str(value)]*df['v_'+str(j)]
        df['new'+str(value)+'+'+str(j)]=df['v_'+str(value)]+df['v_'+str(j)]
        df['new'+str(value)+'-'+str(j)]=df['v_'+str(value)]-df['v_'+str(j)]
 
num_cols1 = [3,5,1,11]
for index, value in enumerate(num_cols1):
    for j in num_cols1[index+1:]:
        df['new'+str(value)+'-'+str(j)]=df['v_'+str(value)]-df['v_'+str(j)]
 
for i in range(15):
    df['new'+str(i)+'*year']=df['v_'+str(i)] * df['car_age_year']

 3.平均数编码

X=df.drop(columns=['price','SaleID','seller','offerType', 'name','creatDate','regionCode'])
Y=df['price']
 
import Meancoder   # 平均数编码
class_list = ['model','brand','power','v_0','v_3','v_8','v_12']
MeanEnocodeFeature = class_list   # 声明需要平均数编码的特征
ME = Meancoder.MeanEncoder(MeanEnocodeFeature,target_type='regression') # 声明平均数编码的类
X = ME.fit_transform(X,Y)   # 对训练数据集的X和y进行拟合

四、建模调参

from catboost import CatBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.metrics import  mean_squared_error
# 划分训练及测试集
x_train,x_test,y_train,y_test = train_test_split( X, Y,test_size=0.3,random_state=1)
# 模型训练
clf=CatBoostRegressor(
            loss_function="MAE",
            eval_metric= 'MAE',
            task_type="CPU",
            od_type="Iter",   #过拟合检查类型
            random_seed=2022)  # learning_rate、iterations、depth可以自己尝试
# 5折交叉  test是测试集B，已经经过清洗及特征工程，方法与训练集一致
result = []
mean_score = 0
n_folds=5
kf = KFold(n_splits=n_folds ,shuffle=True,random_state=2022)
for train_index, test_index in kf.split(X):
    x_train = X.iloc[train_index]
    y_train = Y.iloc[train_index]
    x_test = X.iloc[test_index]
    y_test = Y.iloc[test_index]
    clf.fit(x_train,y_train)
    y_pred=clf.predict(x_test)
    print('验证集MAE:{}'.format(mean_absolute_error(np.expm1(y_test),np.expm1(y_pred))))
    mean_score += mean_absolute_error(np.expm1(y_test),np.expm1(y_pred))/ n_folds
    y_pred_final = clf.predict(test)
    y_pred_test=np.expm1(y_pred_final)
    result.append(y_pred_test)
# 模型评估
print('mean 验证集MAE:{}'.format(mean_score))
cat_pre=sum(result)/n_folds
ret=pd.DataFrame(cat_pre,columns=['price'])
ret.to_csv('/预测.csv')

经过交叉验证取平均值可以将线上分数提高10到15，由于price前期做了对数变换，在预测时需要还原。

五、模型融合

from lightgbm.sklearn import LGBMRegressor
gbm = LGBMRegressor() # 参数可以去论坛参考
# 由于模型不支持object类型的处理，所以需要转化
X['notRepairedDamage'] = X['notRepairedDamage'].astype('float64')
test['notRepairedDamage'] = test['notRepairedDamage'].astype('float64')
result1 = []
mean_score1 = 0
n_folds=5
kf = KFold(n_splits=n_folds ,shuffle=True,random_state=2022)
for train_index, test_index in kf.split(X):
    x_train = X.iloc[train_index]
    y_train = Y.iloc[train_index]
    x_test = X.iloc[test_index]
    y_test = Y.iloc[test_index]
    gbm.fit(x_train,y_train)
    y_pred1=gbm.predict(x_test)
    print('验证集MAE:{}'.format(mean_absolute_error(np.expm1(y_test),np.expm1(y_pred1))))
    mean_score1 += mean_absolute_error(np.expm1(y_test),np.expm1(y_pred1))/ n_folds
    y_pred_final1 = gbm.predict((test),num_iteration=gbm.best_iteration_)
    y_pred_test1=np.expm1(y_pred_final1)
    result1.append(y_pred_test1)
# 模型评估
print('mean 验证集MAE:{}'.format(mean_score1))
cat_pre1=sum(result1)/n_folds
 
#加权融合
sub_Weighted = (1-mean_score1/(mean_score1+mean_score))*cat_pre1+(1-mean_score/(mean_score1+mean_score))*cat_pre

二、下面这个是另外参考的代码，与上面不同

##基础工具
import numpy as np
import pandas as pd
import warnings
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns 
from scipy.special import jn
from IPython.display import display,clear_output
import time
 
#忽略警告信息
warnings.filterwarnings('ignore')
 
##模型预测的
from sklearn import linear_model
from sklearn import preprocessing
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor,GradientBoostingRegressor
 
##数据降维处理的
from sklearn.decomposition import PCA,FastICA,FactorAnalysis,SparsePCA
 
import lightgbm as lgb
import xgboost as xgb
 
##参数搜索和评价的
from sklearn.model_selection import GridSearchCV,cross_val_score,StratifiedKFold,train_test_split
from sklearn.metrics import mean_squared_error,mean_absolute_error
 
#Step2:数据读取
 
##通过pandas对于数据进行读取
Train_data=pd.read_csv('used_car_train_20200313.csv',sep=' ')
TestB_data=pd.read_csv('used_car_testB_20200421.csv',sep=' ')
 
##输出数据的大小信息
#print('Train data shape:',Train_data.shape)
#print('TestB data shape:',TestB_data.shape)
 
##通过.head()简要浏览读取数据的形式(默认前5行)
Train_data.head()
 
##通过.info()简要可以看到对应一些数据列名以及NAN缺失信息
Train_data.info()
 
##通过.columns查看列名
Train_data.columns
 
##通过.describe()可以查看数值特征列的一些统计信息
Train_data.describe()
 
#Step3:特征与标签构建
 
#1)提取数值类型特征列名
numerical_cols=Train_data.select_dtypes(exclude='object').columns
categorical_cols=Train_data.select_dtypes(include='object').columns
 
#2)构建训练和测试样本
##选择特征列
feature_cols=[col for col in numerical_cols if col not in ['SaleID','name','regDate','creatDate','price','model','brand','regionCode','seller']]
feature_cols=[col for col in feature_cols if 'Type' not in col]
 
##提取特征列、标签列构造训练样本和测试样本
X_data=Train_data[feature_cols]
Y_data=Train_data['price']
 
X_test=TestB_data[feature_cols]
 
print('X train shape:',X_data.shape)
print('X test shape:',X_test.shape)
 
##定义了一个统计函数，方便后续信息统计
def Sta_inf(data):
    print('_min:',np.min(data))
    print('_max:',np.max(data))
    print('_mean:',np.mean(data))
    print('_ptp:',np.ptp(data)) #轴方向上的最大值与最小值之差
    print('_std:',np.std(data))
    print('_var:',np.var(data))
 
#3)统计标签的基本分布信息
print('Sta of label:')
Sta_inf(Y_data)
 
##绘制标签的统计图，查看标签分布
#plt.hist(Y_data)
#plt.show()
#plt.close()
 
#4)缺省值用-1填补
X_data=X_data.fillna(-1)
X_test=X_test.fillna(-1)
 
#Step4:模型训练与预测
 
#1)利用xgb进行五折交叉验证查看模型的参数效果
##xgb-Model
xgr=xgb.XGBRegressor(n_estimators=120,learning_rate=0.1,gamma=0,subsample=0.8,\
    colsample_bytree=0.9,max_depth=7) #,objective='reg:squarederror'
 
scores_train=[]
scores=[]
 
##5折交叉验证方式
sk=StratifiedKFold(n_splits=5,shuffle=True,random_state=0)
for train_ind,val_ind in sk.split(X_data,Y_data):
    train_x=X_data.iloc[train_ind].values
    train_y=Y_data.iloc[train_ind]
    val_x=X_data.iloc[val_ind].values
    val_y=Y_data.iloc[val_ind]
 
    xgr.fit(train_x,train_y)
    pred_train_xgb=xgr.predict(train_x)
    pred_xgb=xgr.predict(val_x)
 
    score_train=mean_absolute_error(train_y,pred_train_xgb)
    scores_train.append(score_train)
    score=mean_absolute_error(val_y,pred_xgb)
    scores.append(score)
 
print('Train mean:',np.mean(score_train))
print('Val mean:',np.mean(scores))
 
#2)定义xgb和lgb模型函数
def build_model_xgb(x_train,y_train):
    model=xgb.XGBRegressor(n_estimators=150,learning_rate=0.1,gamma=0,subsample=0.8,\
        colsample_bytree=0.9,max_depth=7) #,objective='reg:squarederror'
    model.fit(x_train,y_train)
    return model
 
def build_model_lgb(x_train,y_train):
    estimator=lgb.LGBMRegressor(num_leaves=127,n_estimators=150)
    param_grid={
        'learning_rate':[0.01, 0.05, 0.1, 0.2],
    } 
    gbm=GridSearchCV(estimator,param_grid)
    gbm.fit(x_train,y_train)
    return gbm
 
#3)切分数据集（Train，Val）进行模型训练，评价和预测
 
##Split data with val
x_train,x_val,y_train,y_val=train_test_split(X_data,Y_data,test_size=0.3)
print('Train lgb...')
model_lgb=build_model_lgb(x_train,y_train)
val_lgb=model_lgb.predict(x_val)
MAE_lgb=mean_absolute_error(y_val,val_lgb)
print('MAE of val with lgb:',MAE_lgb)
 
print('Predict lgb...')
model_lgb_pre=build_model_lgb(X_data,Y_data)
subB_lgb=model_lgb_pre.predict(X_test)
print('Sta of Predict lgb:')
Sta_inf(subB_lgb)
 
print('Train xgb...')
model_xgb=build_model_xgb(x_train,y_train)
val_xgb=model_xgb.predict(x_val)
MAE_xgb=mean_absolute_error(y_val,val_xgb)
print('MAE of val with xgb:',MAE_xgb)
 
print('Predict xgb...')
model_xgb_pre=build_model_xgb(X_data,Y_data)
subB_xgb=model_xgb_pre.predict(X_test)
print('Sta of Predict xgb:')
Sta_inf(subB_xgb)
 
#4)进行两模型的结果加权融合
 
##这里我们采取了简单的加权融合的方式
val_Weighted=(1-MAE_lgb/(MAE_lgb+MAE_xgb))*val_lgb+(1-MAE_xgb/(MAE_xgb+MAE_lgb))*val_xgb
val_Weighted[val_Weighted<0]=10 #由于我们发现预测的最小值有负数，而真实情况下，price为负是不存在的，由此我们进行对应的后修正
print('MAE of val with Weighted ensemble:',mean_absolute_error(y_val,val_Weighted))
 
sub_Weighted=(1-MAE_lgb/(MAE_lgb+MAE_xgb))*subB_lgb+(1-MAE_xgb/(MAE_xgb+MAE_lgb))*subB_xgb
 
##查看预测值的统计进行
plt.hist(Y_data)
plt.show()
plt.close()
 
#5)输出结果
sub=pd.DataFrame()
sub['SaleID']=TestB_data.SaleID
sub['price']=sub_Weighted
sub.to_csv('sub_weighted.csv',index=False)
 
sub.head()

总结

1、二手车预测价格赛题是一个典型的回归问题，要求参赛者根据给定的数据集预测二手车的零售交易价格。

2、数据集通常包括车辆的基本信息、交易时间信息和价格信息等变量，其中可能包含匿名特征。

3、在比赛中，参赛者需要选择合适的机器学习算法或模型，并进行训练和调优，以提高模型的预测准确性。

4、常用的回归算法包括线性回归、逻辑回归、多项式回归、逐步回归、岭回归、套索回归、弹性网络回归等。

5、此外，参赛者还需要进行数据预处理，包括数据清洗、特征工程、缺失值处理等，以确保数据的质量和可用性。

6、同时，对数据进行探索性分析，如可视化、特征相关性分析等，有助于更好地理解数据和选择合适的模型。

7、最终，模型的预测结果将根据平均绝对误差（MAE）等指标进行评估，MAE 值越小，拟合得越好。