Wirtinger derivative: 对复标量求导
Wirtinger derivative: 令
z
=
x
+
j
y
z=x+jy
z=x+jy，则
f
(
z
)
f(z)
f(z) 对
z
z
z 和
z
z
z 的共轭
z
∗
z^*
z∗ 求导结果为
∂
∂
z
=
1
2
(
∂
∂
x
−
i
∂
∂
y
)
\frac{\partial}{\partial z}=\frac{1}{2}\left(\frac{\partial}{\partial x}-i\frac{\partial}{\partial y} \right)
∂z∂=21(∂x∂−i∂y∂)
∂ ∂ z ∗ = 1 2 ( ∂ ∂ x + i ∂ ∂ y ) \frac{\partial}{\partial z^*}=\frac{1}{2}\left(\frac{\partial}{\partial x}+i\frac{\partial}{\partial y} \right) ∂z∗∂=21(∂x∂+i∂y∂)
套用这个公式, 我们有
d
z
d
z
=
1
,
d
z
∗
d
z
=
0
\frac{d z}{d z}=1,~~\frac{d z^*}{d z}=0
dzdz=1, dzdz∗=0
d z 2 d z = 2 z , d z ∗ z d z = z ∗ \frac{d z^2}{d z}=2z,~~\frac{d z^*z}{d z}=z^* dzdz2=2z, dzdz∗z=z∗
Note – 但是这个公式应该有前提是导数存在，因为我们知道，根据定义
d
z
d
z
∗
\frac{d z}{d z^*}
dz∗dz
不存在，但是套公式仍然可以得到
d z d z ∗ = 0 \frac{d z}{d z^*}=0 dz∗dz=0
对于复数向量和矩阵求导，实际操作可以直接查手册，接下来的两节里我们给出两份参考资料。我在实际操作过程中感觉他们已经足够涵盖所有的求导形式了。
复数向量求导参考1
本节来自 https://wenku.baidu.com/view/811c8703e87101f69e319558#
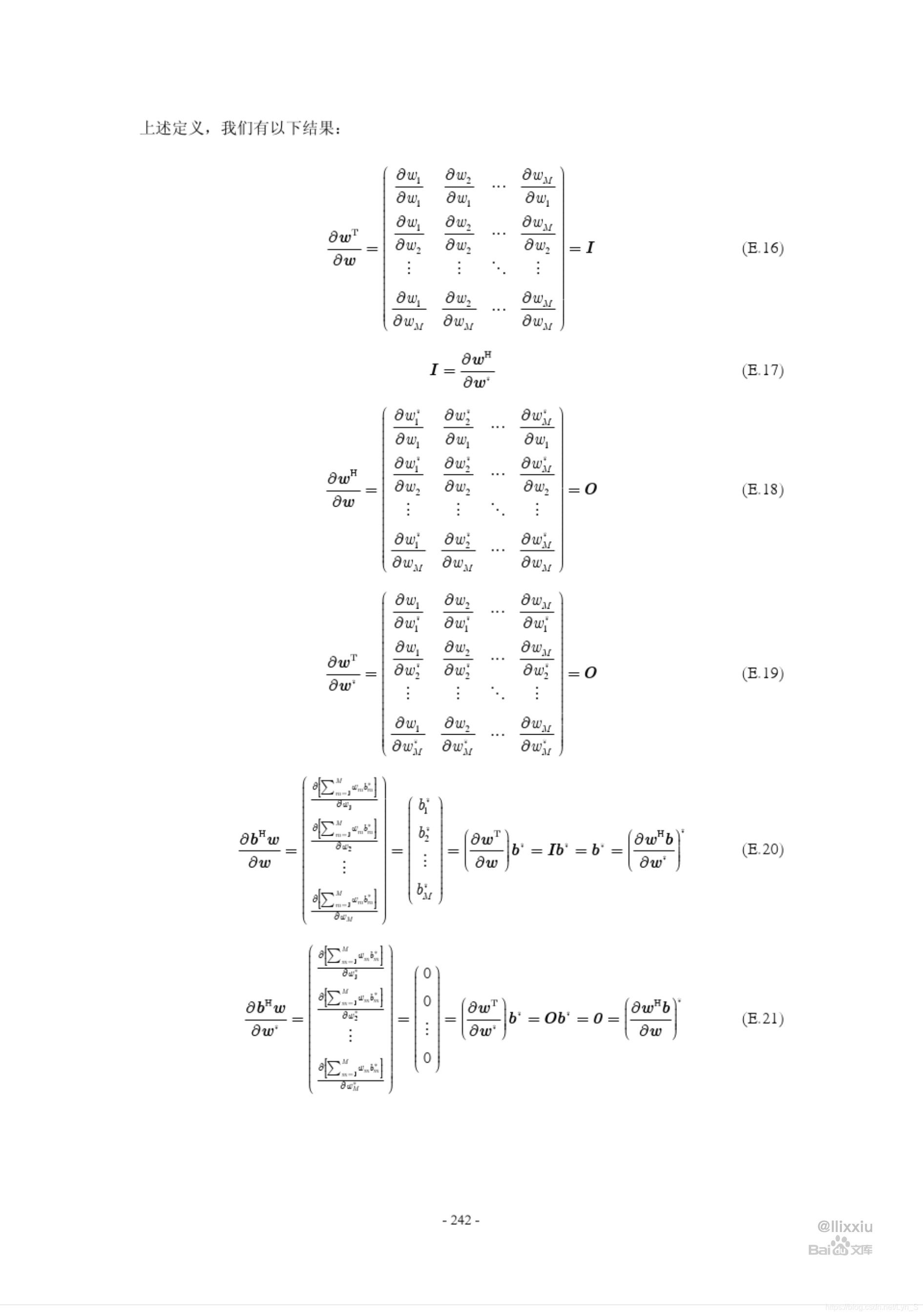
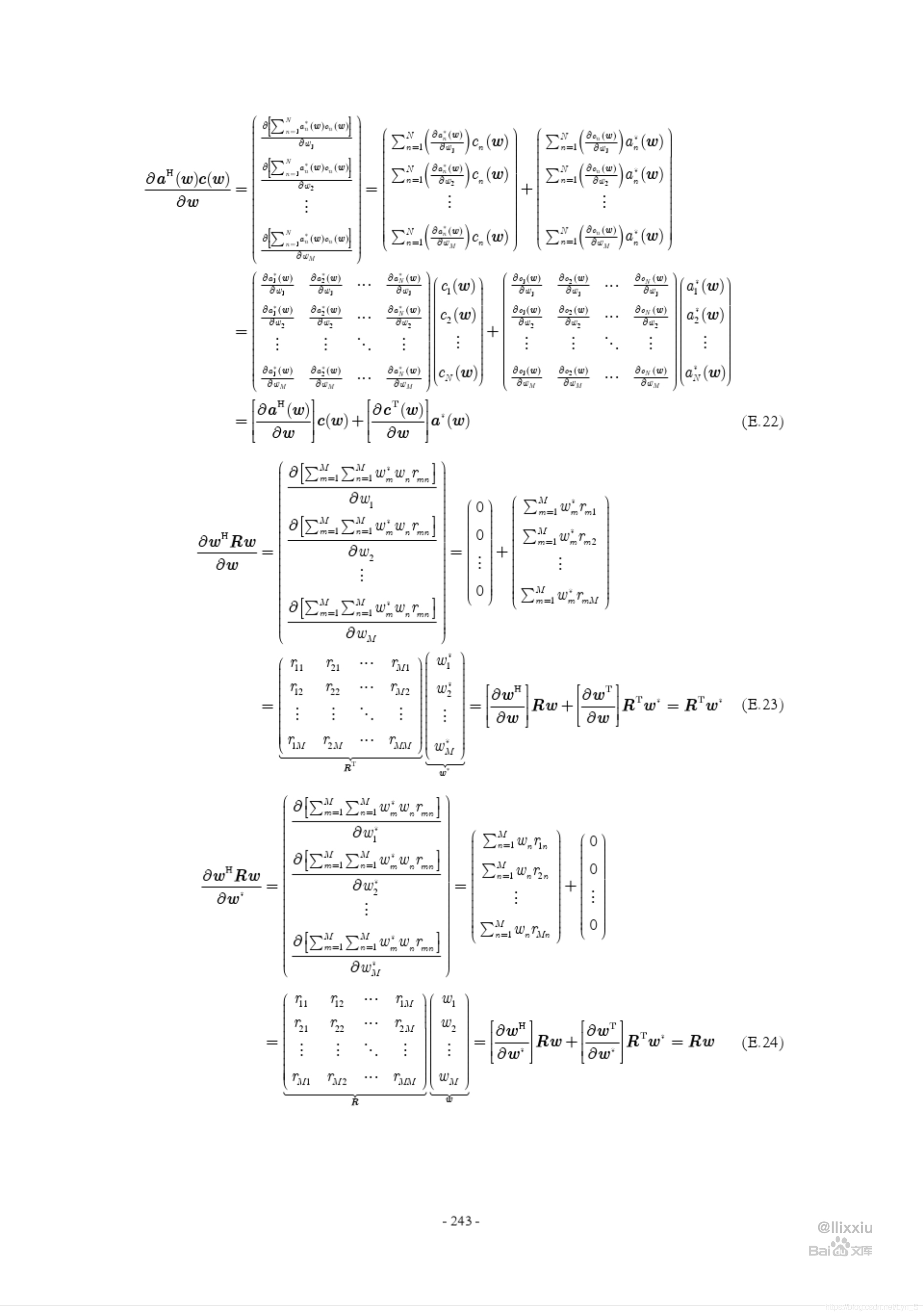
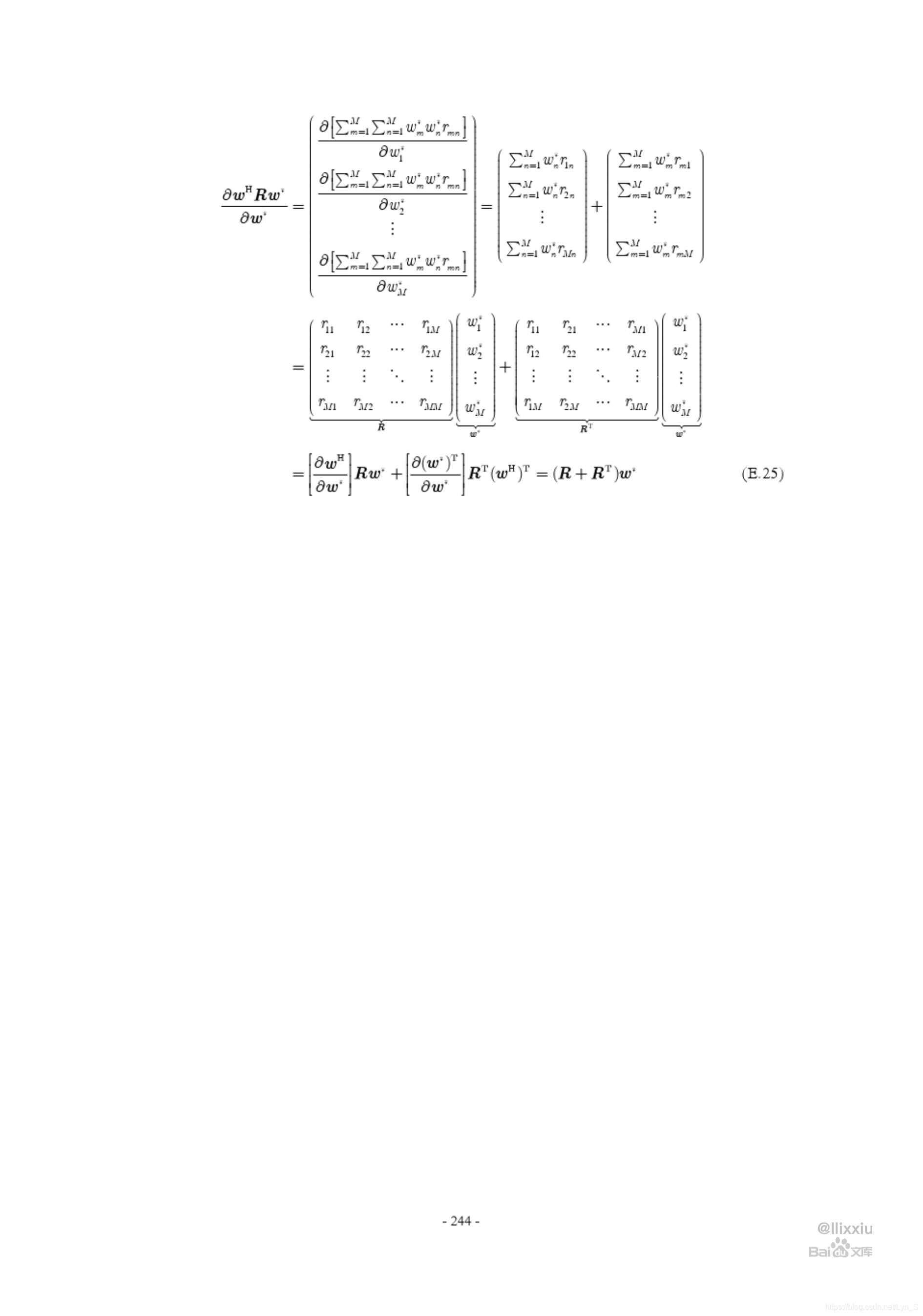
复数向量求导参考2
本节来自 https://www.zhihu.com/question/43657719/answer/96307949
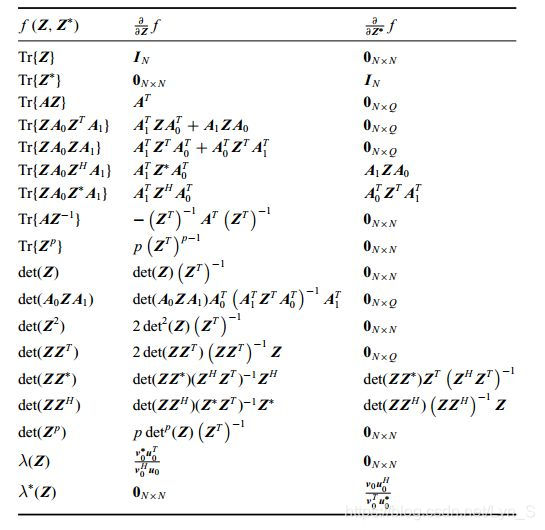
406
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
