一个信息可视化Demo的设计(三):算法设计
作者:愤怒的小狐狸 撰写日期:2012-02-22 ~ 2011-02-28
博客链接: http://blog.csdn.net/MONKEY_D_MENG
此为系列博文,前续请看:
第二部分:《一个信息可视化Demo的设计(二):Index & Search》
一、背景和废话若干
信息可视化一个简单概括性的说法即是将信息、数据、资源等能够通过可视化的手段和方式,直观地呈现给用户,帮助用户梳理其中的知识以及内在关联,必要时提供所见即所得(WYSIWYG)的交互方式。从一个产品设计的角度来考虑的话,好的信息可视化工具必然给用户带来一种自然而然的交互体验,甚至是用户根本没意识到某种交互行为的存在,也即是用户潜意识里面一直在念叨:交互行为不就应该是这样的吗?
作为一个信息可视化的Demo,最终前端的落脚点还是要依托于某种图形化的展示技术来实现。我们的方案是基于Silverlight,当然并不是说我们不可以选用其他的前端技术。正如之前所述,微软一般还是会用自己公司的产品,即便是和我搭档的小伙会用Flex,而我俩都不会Silverlight。插一句题外话,在来实习之前,我还是认为微软的大型在线服务系统如Bing会采用UNIX环境部署,后来得知是基于Win Server,这使我大吃一惊,看来Win Server性能应该还是不错的,虽然我没用过,见笑了各位~
Silverlight提供了交互能力强大且丰富的可视化控件,因此我们有了图形显示、交互的落地技术。然而,同时又有新问题摆在了我们面前,即如何合理地布局一棵树,使得树形结构的渲染简洁而又不失优雅。其实,早在我们刚刚接触这个项目的时候,我还对此不屑一顾,我认为这个项目真是太简单了,说白了不就是把描述Tree的文件载入,把Tree的结构还原,再用Silverlight显示出来嘛。后来,真正做的时候却是问题接踵而来,就比如现在的Tree的布局问题,猛的一看觉得简单的不得了,再仔细一想发现很难一下解决,再到后来看了几个Li给我的老外做的Demo之后,哥彻底清楚过来,如果要想实现的特别NB,还是很难驾驭的。其中,简单一点的Space Tree的Demo链接:http://www.cs.umd.edu/hcil/spacetree/,还有一些比较绚的渲染效果如FishEye Tree、Circular Treemap等,链接:http://www.randelshofer.ch/treeviz/。看完这些Demo你会觉得专业和非专业还是有蛮大差别,是我肯定是想不出这么多、这么绚的效果,而且交互作为黑NB~
对自己有了重新的定位后,我们开始选择最简单的原型设计,即输入一个树,把它完整地在页面上显示出来,使得节点与节点之间的排列布局井然有序简洁优雅而又层次结构关联逻辑清晰可见(- -|||)。那,这应该如何做到呢?说到底还是算法设计问题。
不搞不知道,一搞吓一跳,其实这个问题在几十年前,也就是70年代时候就有NB人物已经解决过了,而且解决的很好。其中比较著名的有Knuth提出的“Optimum binary search trees”,学计算机都知道这人是谁,不用多说。后来,找到一篇论文“Tidy Drawings of Trees”里面介绍了几种方法,感觉比较简单且易于实现,在此做个总结。
二、朴素的树形结构显示算法
首先来看一个朴素的树形结构显示算法,对于任一节点而言,至多存在一个前驱父节点,而根节点root的父节点为NULL,同等高度的节点应处于同一水平线层次。因此,一种朴素方法即是按照节点的高度进行平行绘制,高度可以表征节点的Y轴坐标,计算和获取每个节点高度是首要解决的问题,但在论文中该算法中先假设已经得到了这个值。
算法的基本思路在于将具有相同高度节点的Y轴坐标设置为一样的,即设为高度值,使它们处于同一水平线,剩下的只需要调整它们的X坐标,使得下一个节点的X坐标与上一节点之间存在一定的距离即可,思想是很简单的。
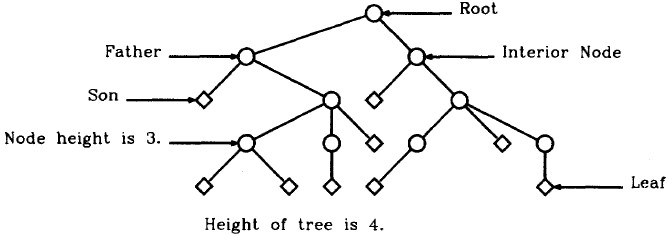
输入:定义良好的树形结构的root、最大高度max_height。
输出:每个节点的坐标(x, y),假设每个节点的高度是已经知道。
算法伪码描述:
//节点数据结构
type node
data; //节点数据
father: branch; //父节点
children_num: integer; //子节点数目
children: array[1..children_num] of branch; //子节点数组
height: integer; //节点高度
x, y: integer; //X、Y轴坐标
status: 0..children_num; //处理子节点数目
end;
//变量定义
var next_x: array[0..max_height] of integer;
current: branch;
i: integer;
begin
//初始化每个高度的X轴首位置为1
for i = 0 to max_height do
next_x[i] = 1;
end for;
//初始化root处理的子节点数目为0
root.status = 0;
current = root;
//结束条件为root的父节点为NULL
while current != NULL do
//首先处理current节点本身
if current.status == 0 then
//X坐标记录在next_x中,用于使同一层次两个节点之间保持间隔
current.x = next_x[current.height];
//Y坐标直接使用节点高度
current.y = 2 * current.height + 1;
//同一层两个节点之间间隔为2
next_x[current.height] = next_x[current.height] + 2;
//初始化所有子节点
for i = 1 to current.children_num do
current.children[i].status = 0;
end for;
//设置current节点已经被处理过
current.status = 1;
//子节点尚未完全处理完
else if 1 <= current.status && current.status <= current.children_num then
current.status = current.status + 1;
current = current.children[current.status - 1];
//子节点处理则回溯到父节点
else current = current.father;
end if;
end while;
end;其实,我并不明白为什么要假设节点的高度是已知的,而事实上我们并不需要提前知道节点的高度,而是可以在计算节点高度的过程中计算节点的(X、Y)坐标值,这一点借助于队列,利用层次遍历的思想很容易就实现了,子节点高度=父节点高度+1嘛,那样给出伪码比论文中给出的还要简单些,其伪码描述如下所示。
输入:定义良好的树形结构的root。
输出:每个节点的坐标(x, y)。
算法伪码描述:
//节点数据结构
type node
data; //节点数据
father: branch; //父节点
children_num: integer; //子节点数目
children: array[1..children_num] of branch; //子节点数组
height: integer; //节点高度
x, y: integer; //X、Y轴坐标
end;
//变量定义
var next_x: array[0..N] of integer;
current: branch;
i: integer;
N: integer;
q: Queue;
begin
//初始化每个高度的X轴首位置为1,N通常取一个较大的数,必须大于树形结构最大高度
for i = 0 to N do
next_x[i] = 1;
end for;
//初始化root的高度为0
root.height = 0;
//将root装入队列
q.push(root);
//如果队列不为空s
while !q.empty() do
//从队列中弹出节点
current = q.pop();
//设置弹出节点的X、Y轴坐标
current.x = next_x[current.height];
current.y = 2 * current.height + 1;
//同一层两个节点之间间隔为2
next_x[current.height] = next_x[current.height] + 2;
//对弹出节点的所有子节点进行处理
for i = 0 to children_num do
//子节点的高度为父节点+1
current.children[i].height = current.height + 1;
//将子节点装入队列
q.push(current.children[i]);
end for;
end while;
end; 按照朴素的树形结构显示算法得绘制的图形如下所示,当然,整体而言还算是比较整齐与简洁,但存在的问题是父子继承关系的连线不太美观与优雅,特别是当某一层次上节点过多时,布局看上去总是不那么Happy,这也是这种方法使用的局限所在。
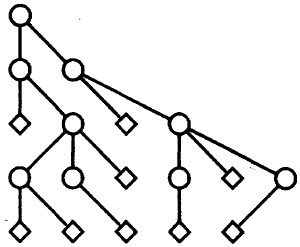
三、二叉树显示算法
二叉树是应用非常广泛的特殊树形结构,其严格意义上并不属于“树”,因为其有明确的左右孩子节点之分,而对于树而言其所有的孩子节点均是平等的。Knuth利用中序遍历的思想,设计了一种二叉树图形渲染算法,基本思路:中序遍历,从而依次确定左孩子、父节点和右孩子节点的坐标。
输入:定义良好的树形结构的root。
输出:每个节点的坐标(x, y),假设每个节点的高度是已经知道。
算法伪码描述:
//节点数据结构
type node
data; //节点数据
father: branch; //父节点
left_son, right_son: branch; //左右孩子节点
height: integer; //节点高度
x, y: integer; //X、Y轴坐标
status: (first_visit, left_visit, right_visit); //遍历的访问模式
end;
//变量定义
var current: branch;
next: integer;
begin
//初始化节点的X坐标
next = 1;
current = root;
current = first_visit;
//存在未处理的二叉树节点
while current != NULL do
//对current的访问情况进行分析
switch current.status
//初次访问模式
case first_visit:
//设定下次访问模式为左访问
current.status = left_visit;
//中序遍历
if current.left_son != NULL then
current = current.left_son;
current.status = first_visit;
end if;
break;
//走到当前子树的最左端,即可确定该节点的X坐标
case left_visit:
current.x = next;
current.y = 2 * current.height + 1;
//计算下一个节点X坐标
++next;
//左边为空,设置右访问模式
current.status = right_visit;
if current.right_son != NULL then
current = current.right_son;
current.status = first_visit;
end if;
break;
//表明右孩子为空,则回溯到父节点
case right_visit:
current = current.father;
break;
end case;
end switch;
end while;
end;Kunth大神的这个算法很是简洁,只需一次中序遍历即确定了所有节点的X坐标,他是使用了一种非递归的方式书写了算法,当然递归的算法描述更为简单:
输入:定义良好的树形结构的root。
输出:每个节点的坐标(x, y),假设每个节点的高度是已经知道。
算法伪码描述:
//变量定义
var current: branch;
next: integer;
//定义中序遍历函数
function in_order(current)
if current != NULL then
in_order(current.left_son);
//计算该节点X坐标
current.x = next++;
current.y = 2 * current.height + 1;
in_order(current.right_son);
end if;
end function;
begin
in_order(root);
end;这种算法存在一个问题,即节点的布局过于分散化,因为所有节点的X坐标都是按照中序遍历的方式叠加上去的,而不存在某些节点具备相同的X坐标值,特别是对于节点之间next间隔设置较大的情况,二叉树的布局就显得不那么美观,如下图所示。

四、整洁二叉树显示算法
根据上述算法存在的问题,我们对节点的布局进行了一些调整和修正,优化了上述的算法使得二叉树节点能够更为紧凑的显示,在节点node的数据节点定义中引入了一个修正器变量,用于美化调整节点渲染布局。
输入:定义良好的树形结构的root。
输出:每个节点的坐标(x, y),假设每个节点的高度是已经知道。
算法伪码描述:
//节点数据结构
type node
data; //节点数据
father: branch; //父节点
left_son, right_son: branch; //左右孩子节点
height: integer; //节点高度
x, y: integer; //X、Y轴坐标
status: (first_visit, left_visit, right_visit); //遍历的访问模式
modifier: integer; //修正器
end;
//变量定义
var modifier: array[0 .. max_height] of integer;
next_pos: array[0 .. max_height] of integer;
i : integer;
place: integer;
h : integer;
is_leaf: boolean;
modifier_sum: integer;
begin
//初始化节点在每层的起始位置为1,且无修正值
for i = 0 to max_height do
modifier[i] = 0;
next_pos[i] = 1;
end for;
current = root;
current.status = first_visit;
while current != NULL do
switch current.staus
//向左孩子遍历
case first_visit:
current.status = left_visit;
if current.left_son != NULL then
current = current.left_son;
current.status = first_visit;
end if
break;
//向右孩子遍历
case left_visit:
current.status = right_visit;
if current.right_son != NULL then
current = current.right_son;
current.status = first_visit;
end if;
break;
//计算该节点位置以及修正值,每层的第一个节点位置均从1开始计
case right_visit:
h = current.height;
is_leaf = (current.left_son == NULL && current.right_son == NULL);
//place是根据子节点计算父节点位置
if is_left then
place = next_pos[h];
else if current.left_son == NULL then
place = current.right_son.x – 1;
else if current.right_son == NULL then
place = current.left_son.x + 1;
else
place = (current.left_son.x + current.right_son.x) / 2;
end if;
//因为每层第一个节点的起始位置都是1,所以需要修正
//计算修正值,即该节点应该往右移动多少距离
modifier[h] = max(modifier[h], next_pos[h] - place);
if is_leaf then
current.x = place;
else
current.x = place + modifier[h];
end if;
//该层次下一节点位置比上一节点向右移动2
next_pos[h] = current.x + 2;
//记录该节点的修正值,代表向右移动的距离
current.modifier = modifier[h];
current = current.father;
break;
end case;
end switch;
end while;
//根据计算得到各节点的X坐标和修正值计算最终的节点位置
current = root;
current.status = first_visit;
modifier_sum = 0;
while current != NULL do
switch current.status
case first_visit:
//父节点记录的修正值,将导致其所有的子节点X坐标向右偏移
current.x = current.x + modifier_sum;
modifier_sum += current.modifier;
current.y = 2 * current.height + 1;
current.status = left_visit;
if current.left_son != NULL then
current = current.left_son;
current.status = first_visit;
end if;
break;
case left_visit:
current.status = right_visit;
if current.right_son != NULL then
current = current.right_son;
current.status = first_visit;
end if;
break;
case right_visit:
//当这个节点所有的子树全部处理完成之后,其修正值则需要复位
//从而不会影响其它子树的向右的偏向量
modifier_sum -= current.modifier;
current = current.father;
end switch;
end while;
end;上述算法先是确定了各节点的X坐标,同时设定了同一层次当中两个相邻节点之间距离为2,由于每一层第一个节点初始X坐标均从1开始,则需要对每个节点设定一个向右移动的修正值,以此形成一棵比较紧凑美观的二叉树。此过程当中,只需要父节点记录整体子树向右需要的偏移量即可,其所有子节点均会按照父节点的修正值完成对应的位移,从而计算出正确的X坐标。下图展示了该算法的具体执行过程,当然这个算法整体读起来还是有那么点绕,不过多看几遍就能懂了,是不是很巧妙啊~
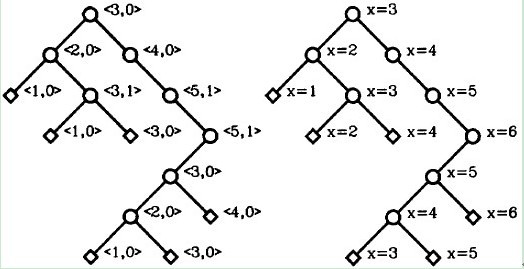
五、表达式查询Search算法设计
我们一般所接触的搜索引擎都是基于关键字的,因为它是一个面向大众的通用搜索平台,而在这个Demo当中,我们却是切合了非常垂直的业务需求,即可以根据任意多个不同的条件短语对信息进行Search,对于表达式的Search操作自然而然提上日程。在博文《一个信息可视化Demo的设计(二):Index & Search》中,已经对Search部分设计进行了简要介绍,本文只要讲解Search表达式的解析,从而能够形成上文中所述的各种Query对象。为简要说明,现在只描述表达式计算算法思想和技巧,参照了数据结构教材里面的内容。
任何一个表达式都是由操作数、运算符和界限符组成的,其中操作数可以是常数也可以是变量或表达式,运算符可以是算术运算符、关系运算符和逻辑运算符等,基本界限符则可以是左右括弧和表达式结束符等。那么一个表达式可以形式化表示为:
Exp(表达式) = D1(操作数) OP(运算符) D2(操作数)则会存在三种表示形式:
OP D1 D2为表达式的前缀表示法
D1 OP D2为表达式的中缀表示法
D1 D2 OP为表达式的后缀表示法
已知表达式Exp = a * b + (c – d / e) * f
前缀表达式:+ * a b * - c / d e f
中缀表达式:a * b + c – d / e * f
后缀表达式:a b * c d e / - f * +
在不同的表示法中,操作数之间的相对次序不变,但运算符之间的相对次序不同。其中,因中缀表达式丢失了原表达式中的括弧信息致使运算的次序不确定,而无法使用,前缀表达式和后缀表达式中都包含了确定的运算顺序。前缀表达式的运算规则为:连续出现的两个操作数和在它们之前且紧靠它们的运算符构成一个最小表达式;后缀表达式的运算规则为:每个运算符和在它之前出现且紧靠它的两个操作数构成一个最小表达式,且运算符在后缀表达式中出现的顺序恰为表达式的运算顺序。可见从后缀式很容易求得表达式的值,只要自左至右的顺序扫描后缀表达式,在扫描的过程中,凡是遇到运算符即作运算,与它对应的操作数应该是在它之前刚刚扫描到的两个操作数。为了识别刚刚扫描过的两个操作数,自然需要一个栈,以实现操作数后出现先运算的规则。算法中以字符串表示算术表达式,表达式尾添加“#”字符作为结束标志。
为了便于简单说明,现在限定操作数以单字母字符作为变量名,自左至右依次识别字符串中的字符,若为字母,则入栈;否则从栈中依次退出第二操作数和第一操作数,并作相应的运算,operate(d1, op, d2)返回d1和d2进行op运算的结果。算法中opMember(char ch)为自定义的返回bool型值的函数,若ch是运算符,则返回True,否则返回False。对于后缀式求得表达式值的算法可概括如下:
//本函数返回由后缀式suffix表示的表达式的运算结果
double evaluation(char suffix[])
{
ch = *suffix++;
initStack(S);
while (ch != ‘#’)
{
//非运算符入操作数栈
if (! opMember(ch)) push(S, ch);
else
{
//两个操作数出栈
pop(S, b); pop(S, a);
//作相应的运算,并将运算结果入栈
push(S, operate(a, ch, b));
}
ch = *suffix++;
}
pop(S, result);
result result;
}现在所剩下的问题即是如何将表达式转换成后缀式了,分析原表达式和后缀式中相应运算符所在不同位置可见,原表达式的运算符在后缀式中出现的位置取决于它本身和后一个运算符之间的优先关系。按照算术运算的规则:(1)先乘除、后加减;(2)从左算到右;(3)先括弧内、后括弧外。因此,可为运算符设置优先数如下:
运算符 # ( + - ) / ^(乘幂)
优先数 -1 0 1 1 2 2 3
当然还有一些比如&&、||等,我们可以自己添加,上述是比较常见的。若当前运算符的优先数小于在它之后的运算符,则暂不送往后缀式,否则它在后缀式中领先于在它后的运算符。换句话说,在后缀式中,优先数高的运算符领先于优先数低的运算符。因此,从原表达式求得后缀式的规则为:
(1)设立运算符栈;
(2)设表达式的结束符为#,预设运算符栈的栈底为#;
(3)若当前字符是操作数,则直接发送给后缀式;
(4)若当前字符为运算符且优先数大于栈顶运算符,则进栈;否则退出栈顶运算符发送给后缀式;
(5)若当前字符是结束符,则自栈顶至栈底依次将栈中所有运算符发送给后缀式;
(6)“(”对它之前的运算符起隔离作用,则若当前运算符为“(”时进栈;
(7)“)”可视为自相应左括弧开始的表达式的结束符,则从栈顶起依次退出栈顶运算符发送给后缀式直至栈顶字符为“)”为止。
//从合法的表达式字符串exp求得其相应的后缀式字符串suffix
void transform(char suffix[], char exp[])
{
//预设运算符栈的栈底元素为#
initStack(S); push(S, ‘#’);
p = exp; ch = *p; k = 0;
while(!stackEmpty(S))
{
//操作数直接发送给后缀式
if (!opMember(ch)) suffix[k++] = ch;
else
{
switch(ch)
{
//左括弧一律入栈
case ‘(’: push(S, ch); break;
case ‘)’: pop(S, c);
while(c != ‘(’)
{ suffix[k++] = c; pop(S, c); }
break;
default:
//precede(a, b)判断运算符的优先程度,当a的优先数>=b的优先数时,返回1;否则返回0
while(getTop(S, c) && precede(c, ch))
{ suffix[k++] = c; pop(S, c); }
if (ch != ‘#’) push(S, ch);
break;
}
}
if (ch != ‘#’) ch = *++p;
}
suffix[k] = ‘\0’;
}当然上述代码对于我们这个Demo还并不是完全适用,我们只是借鉴了这样的处理后缀式的思想,从而把一个Search的表达式语句转化为了Query对象,具体怎样转换,只是在算法的处理细节上有所改变和调整,这块不再描述。
写到这算是把MSRA/STC实习的Demo做了一个整体回顾,从第一篇博文讲架构设计,第二篇博文讲Index & Search,再到这篇博文讲算法设计,虽然不是每个细节都涉及到了,但也差不多了。本来打算把我们做Sliverlight那个平台组件MVC框架也用一个篇幅介绍一下的,但是考虑到现在要面临工作了,可能也很难抽时间去整理了,那咱就有空再说吧~哈哈~





















 3390
3390

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








