P1002 [NOIP2002 普及组] 过河卒

 

题目描述

棋盘上 AA 点有一个过河卒，需要走到目标 BB 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 CC 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，AA 点 (0,0)(0,0)、BB 点 (n,m)(n,m)，同样马的位置坐标是需要给出的。

 

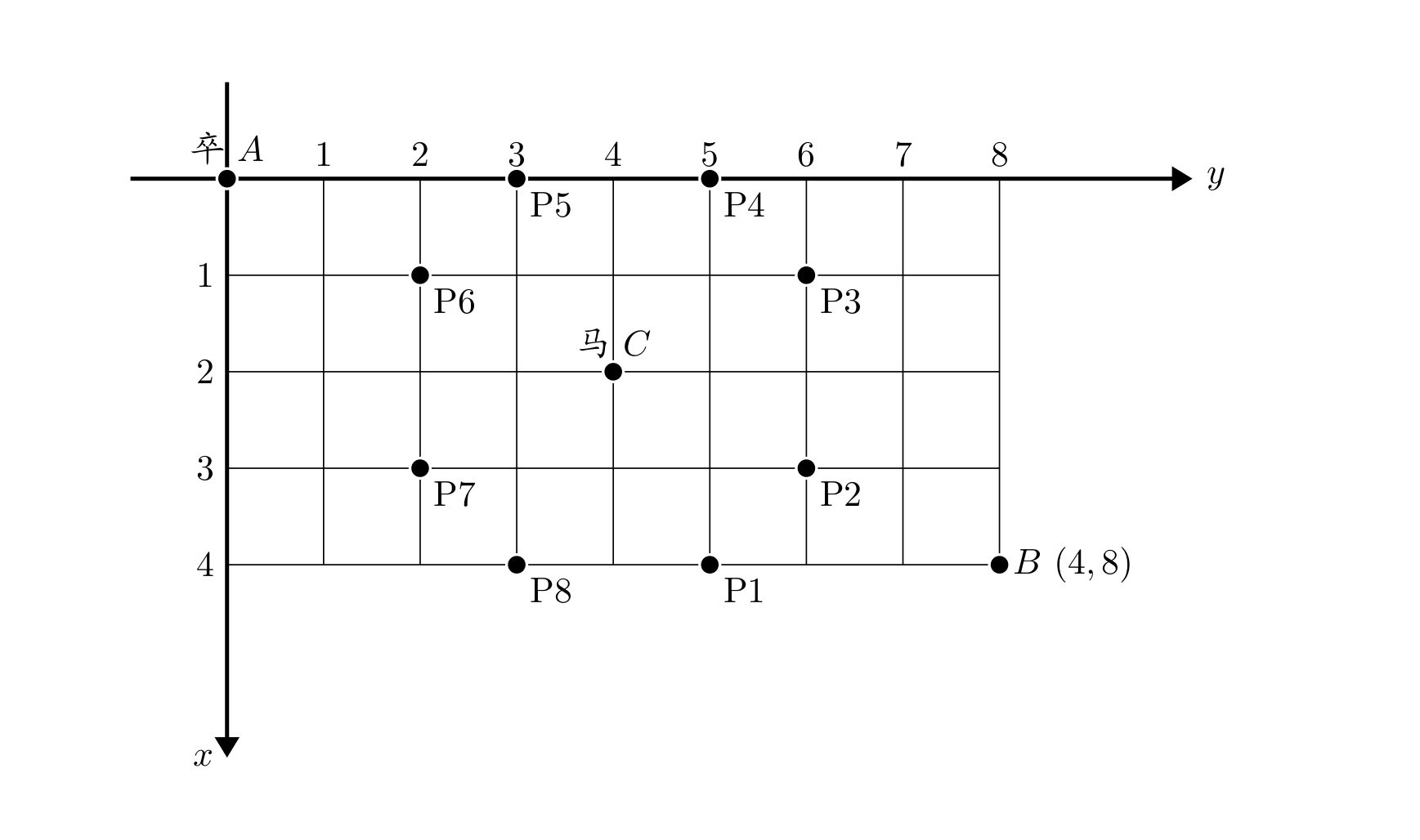
现在要求你计算出卒从 AA 点能够到达 BB 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 BB 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

答案

注意到兵只能向下或者向右移动，所以当前节点的路径条数等于由正上方节点的路径数加上左方节点的路径数相加，如果该点在马的范围内，则直接置为0

//
// Created by skywircL on 1/10/25.
//
#include <cstring>
#include <iostream>
#include <stdio.h>
#include <algorithm> // 需要包含 algorithm 头文件>
#include <cctype>
#include <string>

using namespace std;

void toLowerCase(string &str) {
    transform(str.begin(), str.end(), str.begin(), ::tolower);
}

int num[21][21];
long long dp[21][21];

int main() {
    int m, n, p, q;
    cin >> m >> n >> p >> q;
    if (p - 1 >= 0) {
        num[p - 1][q + 2] = -1;
        if (q - 2 >= 0) {
            num[p - 1][q - 2] = -1;
        }
    }
    if (p - 2 >= 0) {
        num[p - 2][q + 1] = -1;
        if (q - 1 >= 0) {
            num[p - 2][q - 1] = -1;
        }
    }
    if (q - 1 >= 0) {
        num[p + 2][q - 1] = -1;
    }
    if (q - 2 >= 0) {
        num[p + 1][q - 2] = -1;
    }

    num[p][q] = -1;
    num[p + 1][q + 2] = -1;
    num[p + 2][q + 1] = -1;
    dp[0][0] =1;
    for (int i = 0; i <= m; i++) {
        for (int j = 0; j <= n; ++j) {
            if (i == 0) {
                if (j!=0){
                    if (num[i][j]!= -1){
                        dp[i][j]=dp[i][j-1];
                    }else{
                        dp[i][j]=0;
                    }

                }
            }
            if (j == 0) {
                if (i!=0){
                    if (num[i][j]!= -1){
                        dp[i][j]=dp[i-1][j];
                    }else{
                        dp[i][j]=0;
                    }
                }
            }
            if (i!=0&&j!=0){
                if (num[i][j]!=-1){
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                }else {
                    dp[i][j] =0;
                }
            }
            }

    }
    cout<<dp[m][n];

    return 0;
}