费氏搜寻法

说明

二分搜寻法每次搜寻时，都会将搜寻区间分为一半，所以其搜寻时间为O(log(2)n)，log(2)表示

以2为底的log值，这边要介绍的费氏搜寻，其利用费氏数列作为间隔来搜寻下一个数，所以区

间收敛的速度更快，搜寻时间为O(logn)。

解法

费氏搜寻使用费氏数列来决定下一个数的搜寻位置，所以必须先制作费氏数列，这在之前有提

过；费氏搜寻会先透过公式计算求出第一个要搜寻数的位置，以及其代表的费氏数，以搜寻对

象10个数字来说，第一个费氏数经计算后一定是F5，而第一个要搜寻的位置有两个可能，例如

若在下面的数列搜寻的话（为了计算方便，通常会将索引0订作无限小的数，而数列由索引1

开始）：

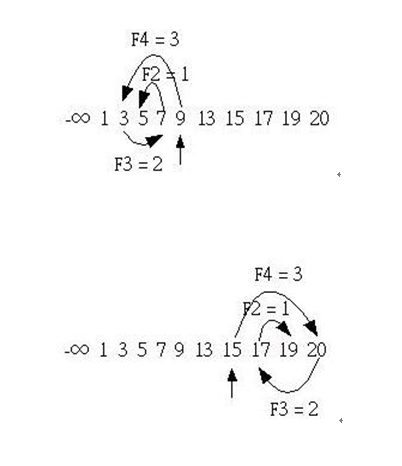
-infin; 1 3 5 7 9 13 15 17 19 20

如果要搜寻5的话，则由索引F5 = 5开始搜寻，接下来如果数列中的数小于指定搜寻值时，就往

左找，大于时就向右，每次找的间隔是F4、F3、F2来寻找，当费氏数为0时还没找到，就表示

寻找失败，如下所示：

由于第一个搜寻值索引F5 = 5处的值小于19，所以此时必须对齐数列右方，也就是将第一个搜

寻值的索引改为F5+2 = 7，然后如同上述的方式进行搜寻，如下所示：

至于第一个搜寻值是如何找到的？我们可以由以下这个公式来求得，其中n为搜寻对象的个数：

Fx + m = n

Fx <= n

也就是说Fx必须找到不大于n的费氏数，以10个搜寻对象来说：

Fx + m = 10

取Fx = 8, m = 2，所以我们可以对照费氏数列得x = 6，然而第一个数的可能位置之一并不是F6，

而是第x-1的费氏数，也就是F5 = 5。

如果数列number在索引5处的值小于指定的搜寻值，则第一个搜寻位置就是索引5的位置，如果

大于指定的搜寻值，则第一个搜寻位置必须加上m，也就是F5 + m = 5 + 2 = 7，也就是索引7的

位置，其实加上m的原因，是为了要让下一个搜寻值刚好是数列的最后一个位置。

费氏搜寻看来难懂，但只要掌握Fx + m = n这个公式，自己找几个实例算一次，很容易就可以理

解；费氏搜寻除了收敛快速之外，由于其本身只会使用到加法与减法，在运算上也可以加快。

 

#include <stdio.h>
#include <stdlib.h>
#define MAX 15
#define SWAP(x,y) {int t; t = x; x = y; y = t;}

void createfib(void);//建立费氏数列
int findx(int, int);// 找x值
int fibsearch(int[], int); // 费氏搜寻
int Fib[MAX] = {-999};
int main(void)
{
    int number[MAX] = {0,2,6,15,23,36,47,55,61,79,83,90,108,120,250};
    int i, find;
    printf("数列：");
    for(i = 0; i < MAX; i++)
        printf("%d ", number[i]);
    printf("\n输入寻找对象：");
    scanf("%d", &find);
    if((i = fibsearch(number, find)) >= 0)
        printf("找到数字索引 %d ", i);
    else
        printf("\n找不到指定数");
    printf("\n");
    return 0;
}
// 建立费氏数列
void createfib(void)
    {
    int i;
    Fib[0] = 0;
    Fib[1] = 1;
    for(i = 2; i < MAX; i++)
        Fib[i] = Fib[i-1] + Fib[i-2];
}
// 找 x 值
int findx(int n, int find)
{
    int i = 0;
    while(Fib[i] <= n)
        i++;
    i--;
    return i;
}
// 费式搜寻
int fibsearch(int number[], int find)
{
    int i, x, m;
    createfib();
    x = findx(MAX+1,find);
    m = MAX - Fib[x];
    printf("\nx = %d, m = %d, Fib[x] = %d\n\n",
    x, m, Fib[x]);
    x--;
    i = x;
    if(number[i] < find)
        i += m;
    while(Fib[x] > 0)
    {
        if(number[i] < find)
            i += Fib[--x];
        else if(number[i] > find)
            i -= Fib[--x];
        else
            return i;
    }
    return -1;
}

//之上系列参考算法大全