Leetcode杨辉三角Ⅱ算法与分析

@Leetcode杨辉三角Ⅱ

趁热打铁，前两天刚刚接触了dp求杨辉三角的小白笔者，今天为大家带来详细的求一行杨辉三角的分析。请看题干：

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

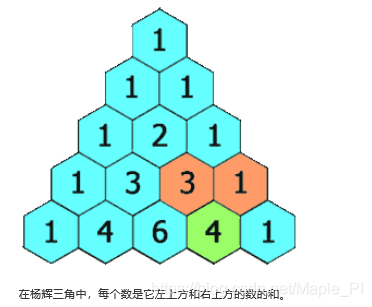
示例:

输入: 3
输出: [1,3,3,1]

所谓一行杨辉三角，顾名思义，就是知道行数，求那一行的解，当然，你大可以把之前的整个二维数组中的最后一部分取出来做为答案交上去，但同时开辟二维vector和一维vector、求出整个三角再要最后一行的做法，未免有点杀鸡用牛刀了，那么若不这么解决，这个问题应该如何考虑呢？请看代码：

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> ans;
        for(int i=0;i<=rowIndex;i++){
            ans.push_back(1);
            for(int j=i-1;j>0;j--){
                ans[j]=ans[j]+ans[j-1];
            }
        }
        return ans;
    }
};

代码短短，但思路十分精彩。笔者太菜，这份代码自然不是笔者亲创，但笔者在此可以对这份代码做一个详细的讲解，相信花了十几分钟认真分析才看出个所以然的coder必然不占少数。

一维可变长数组即可完成本算法，核心思路有二，其一仍然是大家所熟知的杨辉三角的铁则之一——每一个数都是上方两数的和，而另一个神来之笔则是每次判断之时push_back的这个1，那么他到底神奇在哪呢，请听分析：

无论这个rowIndex的值是几，我们会发现，每过一层，可变长数组就会自动＋1，那么第0层和第一层的问题就很好解决了，因为内层循环根本没有执行（不满足j>0),所以当I为1的时候，数组中已经存入了两个1了。

这里要注意一点，这个方法之所以简单，是因为他没有存储得到答案行之前行的数据，但是之前又一定会得到，所以我们要取那一行只需加一个特判条件就能取出来了。

这时候外层循环i来到了2，我们看到，现在数组里有了三个1，内层循环需要执行一次，是将第I-1个位置的数值改为他和他之前一个位置的数值之和，就是这样。


那么现在外层循环来到了I=3，第4个1已经进去了，内层循环需要执行两次，从I-1也就是2号位置开始执行与其前一个数的加和的操作，就像这样：


第二次内层循环则是1号位置：

如此下来，我们会发现，从最后开始加起的数组，每次更新必定会满足杨辉三角的条件，而每次添加的1刚好解决了最右边的1的问题，最左边的1不会经历内循环，故无论是rowIndex值为多少，该算法都能成功执行。

代码虽小，方法确实精妙，大佬们确实牛逼，笔者受教了，原来杨辉三角还有这么多的秘密，也希望大家有所收获哦。