数据结构与算法的关系
个人理解:
数据结构与算法相当于是烹饪食物的整个过程。
数据结构对世界进行了数据化的描述,让现实世界中的人、事、物都抽象出来了,这相当于烹饪过程中的收集食材的过程。
而相应的,算法则是相当于烹饪手法,对食材的各种加工方式,煎、炸、烤等。最终将食材制作成一道道美味的佳肴。
之所以说: 程序 = 数据结构 + 算法
是因为程序的执行者是计算机,而如果计算机获取了需要进行处理的数据内容(数据结构)和对其相应的处理方法(算法)
就能够让计算机完整地实现某项功能了,这便是程序为计算机所带来的功能性。算法的定义
算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或多个操作。
算法相较于数据来说是一种更为抽象的事物,它是一种类似于对经验方法的描述。
是对解决问题的特定方法的描述
它在计算机里的实体表现便是指令序列
这种指令序列中的每一条指令都表示一个或多个操作

指令:(又称机器指令)是指示计算机执行某种操作的命令,是计算机运行的最小功能单位。
为了解决某个或者某类问题,需要把指令表示成一定的操作序列,操作序列包括一组操作,每一个操作都完成特定的功能,这样就组成了一个算法。
算法的特性
算法具有五个基本特性:输入、输出、有穷性、确定性和可行性。
算法本质上是一种描述方法,其具有的性质应该是一种方法能否解决特定问题的前提保证。
输入/输出,是宏观视角来看的,一个方法需要有启动数据和使用这个方法所希望得到的结果。
有穷性其实也是保证这个方法能够输出令人满意的结果。
确定性是建立在能否正确解决特定问题上的前提。
可行性是保证算法实际有效。算法设计的要求
对算法的要求是其具有:正确性、可读性、健壮性、时间效率高和存储量低。
正确性:算法至少应该具有输入、输出和加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。
“正确”的层次:
1.算法程序没有错误
2.算法程序对于合法的输入数据能够产生满足要求的输出结果
3.算法程序对于非法输入能够得到满足规格说明的结果
4.算法程序对于精心选择的,甚至刁难的测试数据都有满足要求的输出结果
为保证相对“正确”和节省开发算法所耗费的精力,一般情况下,我们把层次3作为
一个算法是否正确的标准。
3.算法程序对于非法输入能够得到满足规格说明的结果。可读性: 设计算法需要便于阅读、理解和交流
健壮性:当输入数据不合法时,算法也能做出相关处理,而不是产生异常或莫名其妙的结果。
这要求我们在设计算法时需要考虑对数据的合法性判断。
时间效率高和存储量低:设计算法应该尽量满足时间效率高和存储量低的需求。
算法效率的度量方法
事前统计方法:这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低。
缺点:
- 必须事先编写好程序,需要大量时间和精力
- 时间的比较依赖计算机硬件和软件等环境因素
- 算法的测试数据设计困难
事后分析估算方法:在计算机程序编制前,依据统计方法对算法进行估算。
决定计算机运行时间的因素:
1.算法所采取的策略、方法
2.编译产生的代码质量
3.问题的输入规模
4.机器执行指令的速度
第一条,“算法所采取的策略、方法”是算法好坏的根本。
所以我们可以得出:
一个程序的运行时间,依赖于算法的好坏和问题的输入规模。
总结
测定运行时间最可靠的方法就是计算对运行时间有消耗的基本操作的执行次数。运行时间与这个计数成正比。为此我们不关心编写程序所用的程序设计语言是什么,也不关心这些程序将跑在怎样的计算机中,我们只关心它所实现的算法,这样不计那些循环索引的递增和循环终止条件、变量声明、打印结果等操作,最终,在分析程序的运行时间是,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。
算法的时间复杂度
算法时间复杂度定义:
在进行算法分析时,语句总的执行次数T(n)是关于问题规模 n 的函数,进而分析T(n) 随 n 的变化情况而确定 T(n) 的数量级。算法的时间复杂度,也就是算法的时间量度,记作:T(n) = O(f(n))。它表示问题规模 n 的增大,算法执行时间的增长率和f(n) 的增长率相同,称作算法的渐进时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的某个函数。
一般情况下,随着n的增大,T(n)增长最慢的算法为最优算法。
推导大O阶:
1.用常数1取代运行时间中的所有加法常数
2.在修改后的运行次数函数中,只保留最高阶
3.如果最高阶项存在且不是1,则去除与这个项相乘的常数,得到的结果就是大O阶
常数阶 O(1)
在算法中指令的执行次数都是恒定的,不会随着n的增大而发生变化。
线性阶 O(n)
线性阶的循环结构会比较复杂,我们要分析算法的复杂度,关键就是要分析循环结构的运行情况。
int i;
for(i = 0;i < n; i++)
{
/*时间复杂度为O(1) 的程序步骤序列*/
}对数阶 O(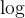 n)
n)
int count = 1;
while(count < n)
{
count = count * 2;
/*时间复杂度为O(1) 的程序步骤*/
}在这里设算法中基本操作执行的次数为 x,所以可以得到 n,因此可以得到
所以这个时间复杂度为O(),注意,这里的底数系数将会变成1.
平方阶O(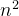 )
)
循环嵌套时一般会出现这样的复杂度
int i,j;
for(i = 0;i < n;i++)
{
for(j = 0; j < n; j++)
{
/*复杂度为O(1)的程序步骤序列*/
}
}在这里每个外层循环一次时,其中内层都要运行n次,而外层总共需要循环n次,所以整体的循环次数就是n * n = .
故嵌套循环的时间复杂度为:O()
想起了一件趣事,前几天在分流班级面试的时候(因为大家都玩了一个暑假再回来,也没对这个面试有足够重视,最后整体情况一言难尽)那个面试的老师问了我一个问题:冒泡排序的时间复杂度是多少?
然后我当时脑子一懵,然后就随便说了一下:O(n)吧。当时我回答完了之后,那位面试的老师嘴角露出笑容,跟我点点头。我看到他这样的表情之后我就以为我的回答是令他满意的,然后就不管了,最后直到面试完后,偷偷拿手机搜索了一下。原来冒泡排序的时间复杂度是O()。
所以我至今都不知道为什么那位老师为什么要露出这样的笑容。
几个思考问题:
int i ,j;
for(i = 0;i < n ; i++)
{
for(j = i; j < n; j++)
{
/*时间复杂度为O(1)的程序步骤序列*/
}
}先把i在不同取值时,每层程序运行的次数。
i = 0 内循环执行了n次
i = 1 内循环执行了n-1次
i = 2 内循环执行了n-2次
...
i = n-1 内循环执行了1次
所以总的执行次数:
我们再利用推导大O阶的方法。第一条,没有加法常数不考虑;第二条,只保留最高项,所以保留;第三条,去除这个相乘的常数,最终可以得到这段代码的时间复杂度为O(
)。
对于方法调用的时间复杂度分析:
int i ,j;
for(i = 0; i < n; i++)
{
function(i);
}
//调用函数
void function(int count)
{
print(count);
}在这里可以先分析主函数中,程序步骤序列的时间复杂度,即代码中function函数的时间复杂度。显然function的时间复杂度为O(1),这样就变成和上方带有循环的代码段相同了,所以整体的时间复杂度为O(n)。
再进行更复杂的思考,把上面的function函数内容进行修改:
void function(int count)
{
int j;
for(j = count;j < n; j++)
{
/*时间复杂度为 O(1)的程序步骤序列*/
}
}同样的,先对函数进行分析,这里的function函数的时间复杂度应该是O(n),这相当于讲一个循环嵌套在另一个循环里面,所以整体的时间复杂度为O()。
下面是一段更复杂的代码
void function(int count)
{
print(count);
}n++; //执行次数为1
function(n); //执行次数为n
int i,j;
for(i = 0;i < n; i++) //执行次数为n*n
{
function(i);
}
for(i = 0;i < n; i++) //执行次数为n(n+1)/2
{
for(j = 0;j < n; j++)
{
//时间复杂度为O(1)的程序步骤序列
}
}它的执行次数,所以这段代码的时间复杂度应该是O(
)。
常见的时间复杂度
| 执行次数函数 | 阶 | 非正式术语 |
|---|---|---|
| O(1) | 常数阶 | |
| O( | 线性阶 | |
| O( | 平方阶 | |
| O( | 对数阶 | |
| O( | ||
| O( | 立方阶 | |
| O( | 指数阶 |

对算法的分析,一般在没有特殊说明的情况下,都是指最坏的时间复杂度。
空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式为:
S(n) = O(f(n))
n为问题规模,f(n) 为语句关于n所占内存空间的函数























 2489
2489

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








