提要:视频版BV1zpPRenEFq附程序链接
我们现在以左下角的转盘为例。
这个转盘的六个奖项的分值和每个奖项的概率我分别将其设为s和p
| i | p(i) | s(i) |
| 0 | 2% | 8888 |
| 1 | 6% | 0 |
| 2 | 8% | 3288 |
| 3 | 15% | 2688 |
| 4 | 19% | 0 |
| 5 | 50% | 1288 |
一般来说,我们可以通过计算数学期望的方式来进行估计一次能赚多少积分
也就是:
![]()
即:

算出的结果就是:1488积分/局
但是你别忘了,玩一局我想我们需要的结果是一个币平均下来能抵多少积分
这个转盘需要300游园币,打一局气球只需要30游园币
简单除一下就是:
左下角转盘:4.96积分/币,打气球:6.5333…积分/币
显然是打气球更高
……是吗?
我们回过头来审视一下这个公式:

你能看出来这公式藏着40次保底吗?
我翻来覆去也看不出来,字里行间没一句和40沾边
但是我们能确定的是,抽40次是至少中大奖一次的
而大奖和积分有关的转盘只有这一个,我想我们不能不考虑这个保底
毕竟原公式就是一个马尔科夫链
除了赛尔号的策划,应该没什么古神会把这玩意做进关卡里面吧(心虚)
我仍然用这个转盘为例,现在我们要算上保底的40次,应该对这个公式进行调整
这是在不考虑保底的情况下,转一次的期望积分:

我们换一个角度思考:保底40次的意思是什么呢?
不是疯狂星期4V我50(恼)
而是40次内中奖的概率为1
“40次内中奖”这个事件可以拆成40个子事件:都是第𝑖i次中奖
每一个子事件所对应的数学期望都不一样
更何况我们还要进一步计算每一游园币能抵多少积分的期望
首先我们来看一个简单的:第一次中头等奖的概率毋庸置疑就是0.02
那么第二次中头等奖的概率呢?只要第一次不中且第二次中就好了,是0.98乘以0.02
那么第五次中头等奖的概率呢?只要前四次不中且第五次中就好了,是0.98的四次方再乘以0.02
一般地,第i次中头等奖的概率就是![]()
不过要注意,第40次和第41次分别是什么?不是直接i=40,41往里代,第40次的概率是1,第41次的概率在这里没有研究的意义
![]()
![]()
现在,我们来算第𝑖i次中头等奖的数学期望
因为第i次中头等奖要求我们前i-1次必定不中头等奖
那么,前𝑖−1次的期望得分不能带头等奖那p(0)的概率玩,每一局的期望得分应为

不过,因为第𝑖i次才中奖,那么前𝑖−1i-1次抽中其他奖项的概率要大那么一点
因为我们已经知道那0.02的地方是不可能的了,就相当于前𝑖−1次是在其余5个地方选择,那么期望调整为  这边可以用面积法来理解,原来的总面积是1,现在的总面积是1-p(0),而每一块的面积仍然是 p(j)
这边可以用面积法来理解,原来的总面积是1,现在的总面积是1-p(0),而每一块的面积仍然是 p(j)

考虑到还要上机编码计算方便,我这里把左下角视作第三个转盘
300就变为一个数组的元素:cost(2)
同样的,p(i)s(i)要作为第三个的东西,要变成二维数组p(2,j)s(2,j)

在前i-1次都不中的前提下,第i次中头等奖的概率是1,同等的,也需要花费cost(2)才能进行第i次
那么只需要在上一个公式前面加一个第i次就可以了

别忘了这是i次一共的结果,我们还要除以𝑖i来转化为一次的量
毕竟我们最终要比较的归根结底还是一局之内每个游园币能抵多少积分的期望
即:

最后再乘上发生第i 次才中头等奖的概率得:

最后的最后,第40次单独计算,因为这一次没有末尾的p(2,0)再乘上发生第i次才中头等奖的概率得:

为了上机编码计算方便,我将保底的40记作一个数组元素n(2)


------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
接下来谈谈代码的问题,这次计算是基于vb6的,为了便于展示和使用,我设计了2个窗体

主窗体的作用是模拟抽奖以及保存模拟抽奖的记录;第二个窗体的作用就是展示计算过程。
Dim p%(3, 5), s%(3, 5), n%(3), k#(3), x#(3), cost%(3)上面的代码是主窗体通用部分的声明,用于声明所需数组
Dim p#(3, 5), s%(3, 5), n%(3), k#(3), x#(3), cost%(3)
Const str1 = "分/币"上面的是声明用于计算的窗体所需的数组和常量
Private Sub Form_Load()
Form1.AutoRedraw = True
If Dir(Text1.Text, vbDirectory + vbNormal) = "" Then MkDir (Text1.Text)
p0 = Array(2, 2, 10, 12, 24, 50)
p1 = Array(2, 7, 7, 10, 24, 50)
p2 = Array(2, 6, 8, 15, 19, 50)
p3 = Array(2, 4, 10, 10, 24, 50)
s0 = Array(0, 0, 1666, 0, 0, 888)
s1 = Array(0, 2666, 0, 1666, 0, 666)
s2 = Array(8888, 0, 3288, 2688, 0, 1288)
s3 = Array(0, 1266, 0, 888, 0, 666)
For i = 0 To 3
For j = 0 To 5
Select Case i
Case 0
p(i, j) = p0(j)
s(i, j) = s0(j)
n(i) = 30
cost(i) = 120
Case 1
p(i, j) = p1(j)
s(i, j) = s1(j)
n(i) = 30
cost(i) = 120
Case 2
p(i, j) = p2(j)
s(i, j) = s2(j)
n(i) = 40
cost(i) = 300
Case 3
p(i, j) = p3(j)
s(i, j) = s3(j)
n(i) = 20
cost(i) = 80
End Select
Next j
Next i
End Sub这个是主窗体的form_load事件,难点在于vb6没法像C和Java那样快速声明多维数组,我本来想用matlab来操作的,但是时间久了,具体的语法已经忘得差不多了,再加上时间比较赶,就用了平时熟悉的语言来写。另外一个窗体的form_load事件大同小异,不再过多赘述。
Private Sub Command1_Click(Index As Integer)
Dim range%(5), x%, filename$, str1$, res%, sum#, arr%(), bigShot%
ReDim arr%(1 To Int(HScroll1.Value))
sum = 0
bigShot = 0
Select Case Index
Case 0
filename = Text1.Text + "左上" + Str(Int(HScroll1.Value)) + "次-" + Format(Now, "yyyymmddhhmmss") + ".txt"
Case 1
filename = Text1.Text + "右上" + Str(Int(HScroll1.Value)) + "次-" + Format(Now, "yyyymmddhhmmss") + ".txt"
Case 2
filename = Text1.Text + "左下" + Str(Int(HScroll1.Value)) + "次-" + Format(Now, "yyyymmddhhmmss") + ".txt"
Case 3
filename = Text1.Text + "右下" + Str(Int(HScroll1.Value)) + "次-" + Format(Now, "yyyymmddhhmmss") + ".txt"
End Select
range(0) = p(Index, 0)
For i = 1 To 5
range(i) = p(Index, i) + range(i - 1)
Next i
For i = 1 To Int(HScroll1.Value)
Randomize
x = Int(Rnd * 100 + 1)
If x <= range(0) Then
res = s(Index, 0)
bigShot = bigShot + 1
ElseIf x > range(0) And x <= range(1) Then
res = s(Index, 1)
ElseIf x > range(1) And x <= range(2) Then
res = s(Index, 2)
ElseIf x > range(2) And x <= range(3) Then
res = s(Index, 3)
ElseIf x > range(3) And x <= range(4) Then
res = s(Index, 4)
'Case x > range(4)
Else
res = s(Index, 5)
End If
arr(i) = res
sum = sum + res
Next i
sum = sum / Int(HScroll1.Value) / cost(Index)
Open filename For Output As #1
str1 = "本次" + Str(Int(HScroll1.Value)) + "次,每次" + Str(cost(Index)) + "游园币,平均" + Str(sum) + "积分/币。其中有" + Str(bigShot) + "次大奖"
Print #1, str1
For i = 1 To Int(HScroll1.Value)
Print #1, arr(i)
Next i
Close #1
MsgBox sum, , "平均多少积分/币"
MsgBox bigShot, , "头等奖次数"
MsgBox "结果已存至" + filename, , "提示"
End Sub上面是主窗体的Command1_Click事件,通过控件数组的index的值来确定转的是哪个转盘。
Private Sub Command1_Click(Index As Integer)
Dim res1#, res2#, c1#
res1 = (k(Index) + p(Index, 0) * s(Index, 0)) / cost(Index)
c1 = p(Index, 0) / x(Index) / cost(Index)
res2 = c1 * y1(x(Index), Index) + (x(Index) ^ (n(Index) - 1)) * ((n(Index) - 1) * k(Index) / cost(Index) / x(Index) + s(Index, 0) / cost(Index)) / n(Index)
Picture1.Cls
Picture1.Print "不计保底:" + Trim(Str(Round(res1, 4))) + str1
Picture1.Print
Picture1.Print
Picture1.Print "计对应保底:" + Trim(Str(Round(res2, 4))) + str1
End Sub上面是计算窗体的Command1_Click事件,同样采取了控件数组的方式。
看上去很简洁(大概?)不只是说我把一些保留错误尝试的注释删了,复杂的计算过程被我简化成几个不同的系数相乘了,至于res2那边莫名其妙的y函数是啥?其实就是秦九韶算法计算线性多项式的值被我打包成了一个函数y,具体如下:
Function y1#(x, nn)
Dim m0#, m1#, c#, j#
m0 = 0
m1 = ((n(nn) - 2) * k(nn) / x + s(nn, 0)) / (n(nn) - 1)
For i = 2 To n(nn) - 1
j = n(nn) - i
c = (j - 1) * k(nn) / x + s(nn, 0)
m0 = c / j
m1 = Round(x * m1 + m0, 4)
Next i
y1 = m1 * x
End Function来看运算结果吧,下面四张图片依次为↖↗↙↘

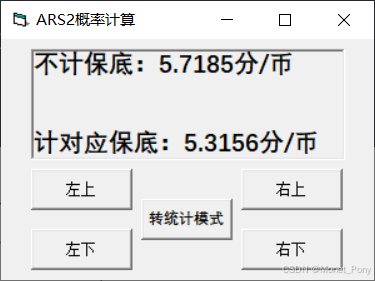
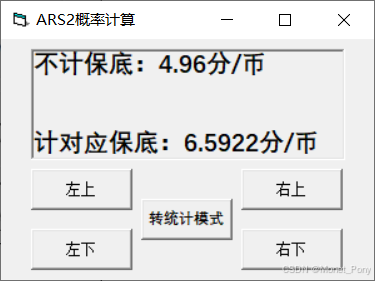

码到这里也就差不多了,这个模型我调试过多次,应该可以评价:这个模型可能有问题,但这个模型有问题有的不太可能
我私自调整了左下角转盘的保底次数,一开始保底次数越大收益越大,这很明显有问题,后来调整过之后,次数越多收益越小,看起来没什么问题了。但是在实际的模拟程序中,这个转盘的收益期望还是接近不计保底的量,但是凭借我的统计学水平和代码水平来看,这个小项目没法再继续下去了,我甚至还问了gpt4,但是gpt4仿佛是个滞胀,怎么问它都是1-p(0)的多少次方,它理解不了一点(恼)
现在的我已经很疲惫了,连视频展示都懒得做了,再鼓足劲继续,怕不是再过寥寥几天假期结束后我一副快寄了模样面对新的**的一年了(恼)
如果有大佬愿意仔细看看并给出意见甚至是指正,那我肯定是螺旋升天爆炸式欢迎的(笑)























 289
289

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








