神经网络
1. 神经元模型
神经网络(neural network)中最基本的成分是神经元(neuron)。
- M-P神经元模型:

在这个神经元中:
他接收来自n个其他神经元传递过来的输入信号,且每个信号都有一个权重,其接收到的总输入值( ∑ i = 1 n ω i x i \displaystyle \sum_{i=1}^n\omega_ix_i i=1∑nωixi)与神经元的阈值(threshold)进行比较,然后通过激活函数(activation function)处理以产生神经元的输出。
- 激活函数(activation function):
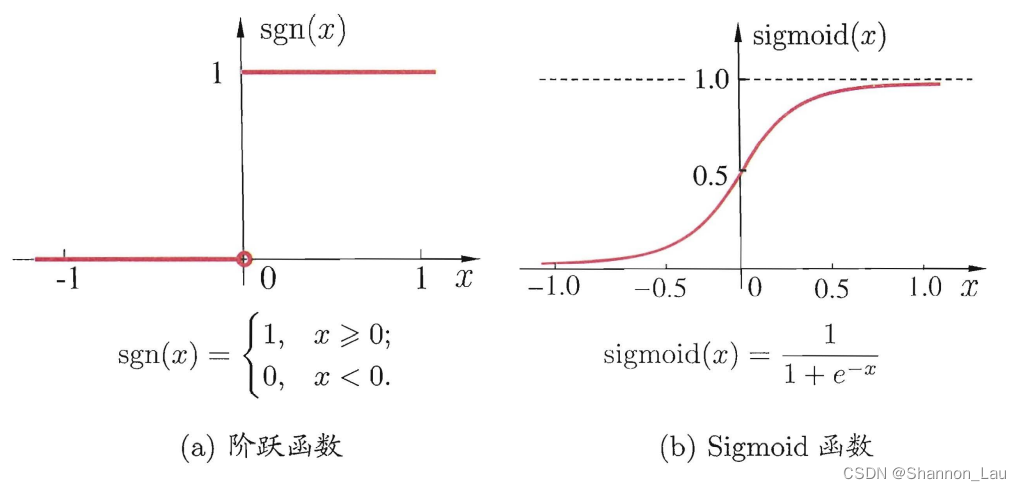
- 阶跃函数:
将输入值映射为0(神经元抑制)、1(神经元兴奋)。缺点是不连续、不光滑。
- Sigmoid函数:
把可能在较大范围内变化的输入值挤压到(0,1)输出值范围内,也称为 “挤压函数” (squashing function).
神经网络由许多这样的神经元按照一定的层次结构连接起来。
将神经网络视为一个包含了许多参数的数学模型,这个模型是若干个函数,例如 y j = f ( ∑ i ω i x i − θ j ) y_j=f( \sum_i\omega_ix_i-\theta_j) yj=f(∑iωixi−θj)相互嵌套而得。
2. 感知机与多层网络
感知机(Perceptron)由两层神经元组成。
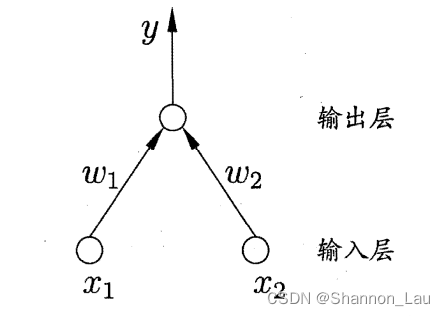
输入层接收外界信号后传递给输出层,输出层是M-P神经元,亦称”阈值逻辑单元“(threshold logic unit).
感知机能很容易实现逻辑与、或、非运算。(但是不能实现异或XOR)
- ”与“( x 1 ⋀ x 2 x_1 \bigwedge x_2 x1⋀x2)
ω 1 = ω 2 = 1 , θ = 2 , 则 y = f ( 1 ⋅ x 1 + 1 ⋅ x 2 − 2 ) , 仅 在 x 1 = x 2 = 1 时 , y = 1 \omega_1=\omega_2=1,\theta=2,则y=f(1·x_1+1·x_2-2),仅在x_1=x_2=1时,y=1 ω1=ω2=1,θ=2,则y=f(1⋅x1+1⋅x2−2),仅在x1=x2=1时,y=1
- ”或“( x 1 ⋁ x 2 x_1 \bigvee x_2 x1⋁x2)
ω 1 = ω 2 = 1 , θ = 0.5 , 则 y = f ( 1 ⋅ x 1 + 1 ⋅ x 2 − 0.5 ) , 仅 在 x 1 = 1 或 x 2 = 1 时 , y = 1 \omega_1=\omega_2=1,\theta=0.5,则y=f(1·x_1+1·x_2-0.5),仅在x_1=1或x_2=1时,y=1 ω1=ω2=1,θ=0.5,则y=f(1⋅x1+1⋅x2−0.5),仅在x1=1或x2=1时,y=1
- ”非“( ¬ x 1 \neg x_1 ¬x1)
ω 1 = − 0.6 , ω 2 = 0 , θ = − 0.5 , 则 y = f ( − 0.6 ⋅ x 1 + 0 ⋅ x 2 − 0.5 ) , 当 x 1 = 1 时 , y = 0 ; x 1 = 0 时 , y = 1 \omega_1=-0.6,\omega_2=0,\theta=-0.5,则y=f(-0.6·x_1+0·x_2-0.5),当x_1=1时,y=0;x_1=0时,y=1 ω1=−0.6,ω2=0,θ=−0.5,则y=f(−0.6⋅x1+0⋅x2−0.5),当x1=1时,y=0;x1=0时,y=1
给定训练数据集,权重 ω i ( i = 1 , 2 , . . . , n ) 以 及 θ \omega_i(i=1,2,...,n)以及\theta ωi(i=1,2,...,n)以及θ可以通过学习得到。阈值 θ \theta θ可以看作一个固定输入为-1.0的”哑结点“(dummy node)所对应的连接权重 ω n + 1 \omega_{n+1} ωn+1。这样就把权重和阈值的学习统一为权重的学习。
对于训练样例
(
x
,
y
)
(x,y)
(x,y),若当前感知机的输出为
y
^
\hat{y}
y^,则感知机会这样调整:
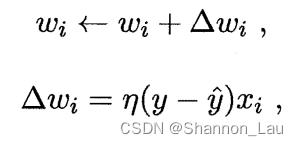
其中
η
∈
(
0
,
1
)
\eta \in (0,1)
η∈(0,1)称为学习率(learning rate)。
若感知机对 ( x , y ) (x,y) (x,y)预测正确,即 y ^ = y \hat{y}=y y^=y,则感知机不发生变化,否则将根据错误的程度进行权重调整。
感知机只有输出层神经元进行激活函数处理,就只拥有一层功能神经元(functional neuron),学习能力很有限。
上述的与、或、非问题都是线性可分(linearly separable)的问题,即存在一个超平面能把他们分开,则感知机的学习过程一定会收敛(converge)而求得适当的权向量
ω
=
(
ω
1
;
ω
2
;
.
.
.
;
ω
n
+
1
)
\omega=(\omega_1;\omega_2;...;\omega_{n+1})
ω=(ω1;ω2;...;ωn+1);否则感知机学习过程会发生振荡(fluctuation),
ω
\omega
ω难以稳定,不能求得合适解,例如感知机不能解决异或这样的非线性可分问题。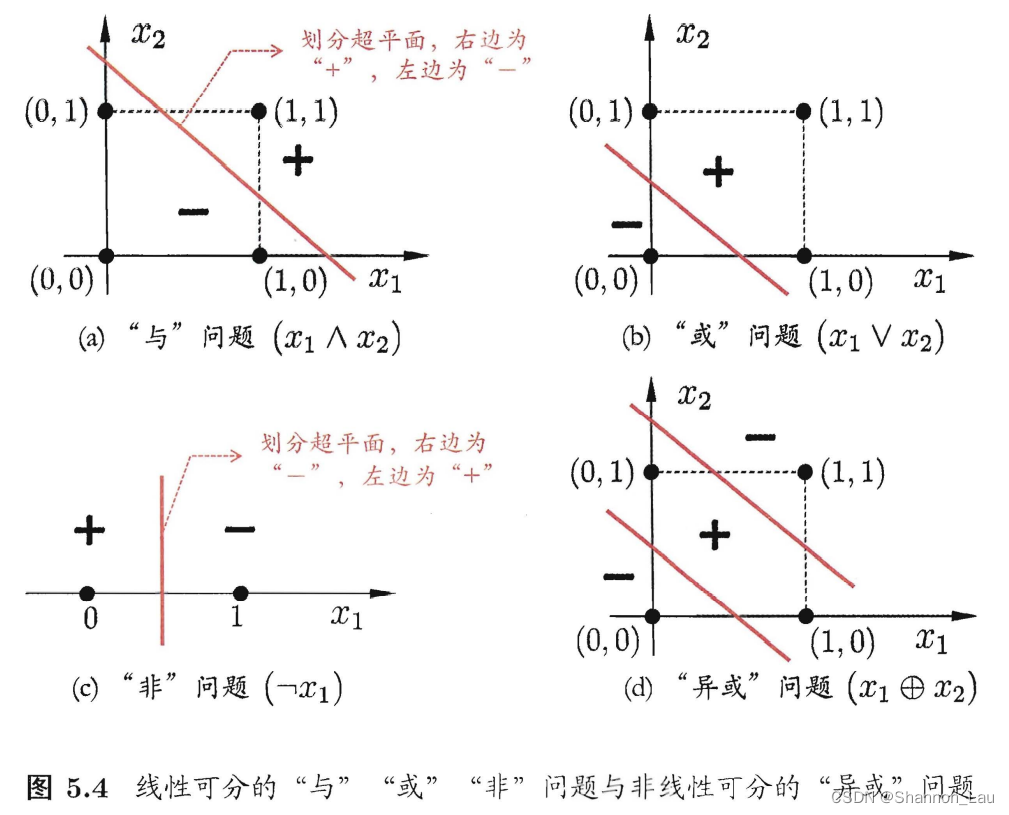 为了解决非线性可分问题,需要使用多层功能神经元。
为了解决非线性可分问题,需要使用多层功能神经元。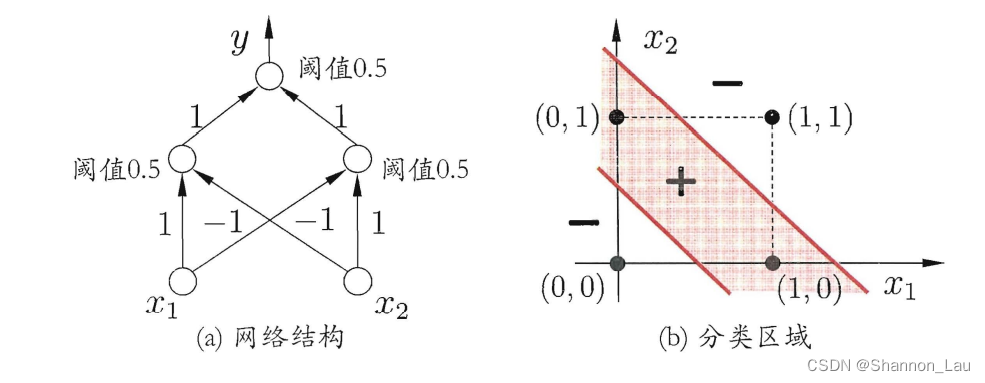
输入层与输出层之间的被称为隐层或隐藏层(hidden layer),隐藏层和输出层神经元都是拥有激活函数的功能神经元。
多层前馈神经网络(multi-layer feedforward neural networks):每层神经元与下一层神经元全连接,不存在同层连接、跨层连接。
输入层神经元接受外部输入,隐藏层与输出层神经元对信号进行加工,最终由输出神经元输出结果。
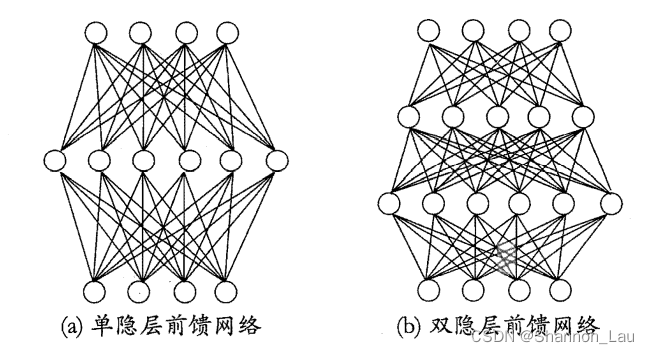
输入神经元仅接收输入,不进行函数处理,隐藏层与输出层含有功能神经元。因此,上图(a)常被成为”两层网络“,也成为”单隐藏层网络“。
神经网络的学习过程就是根据训练数据来调整神经元之间的连接权(connection weight)以及每个功能神经元的阈值;换言之,神经网络“学”到的东西,蕴含在连接权和阈值中。
3. 反向传播算法
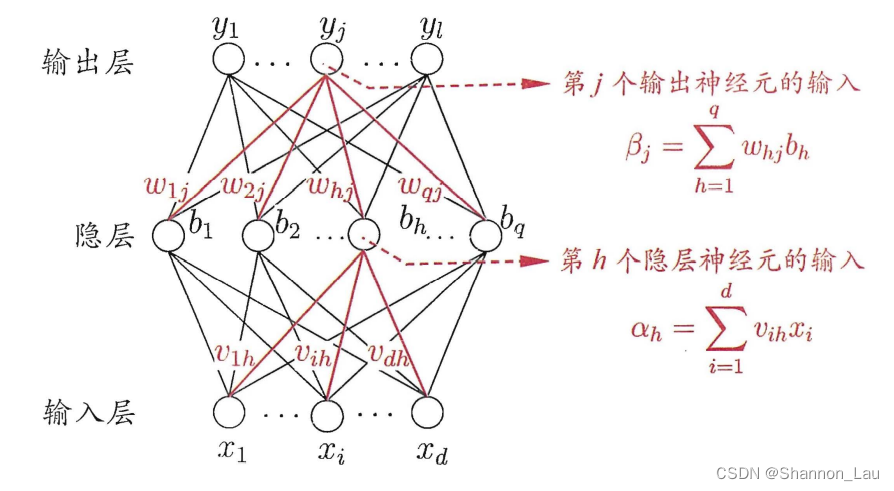
d d d个输入神经元、 l l l个输出神经元、 q q q个隐层神经元。
θ j \theta_j θj:输出层第 j j j个神经元的阈值
γ h \gamma_h γh:隐层第 h h h个神经元的阈值
v i h v_{ih} vih:输入层第 i i i个神经元与隐层第 h h h个神经元之间的连接权。
ω h j \omega_{hj} ωhj:隐层第 h h h个神经元与输出层第 j j j个神经元之间的连接权。
α h = ∑ i = 1 d v i h x i \alpha_h=\displaystyle \sum_{i=1}^dv_{ih}x_i αh=i=1∑dvihxi:隐层第 h h h个神经元接收到的输入。
β j = ∑ h = 1 q ω h j b h \beta_j=\displaystyle \sum_{h=1}^q\omega_{hj}b_h βj=h=1∑qωhjbh:输出层第 j j j个神经元接收到的输入。
b h b_h bh:为隐层第 h h h个神经元的输出。
对于训练例 ( x k , y k ) (x_k,y_k) (xk,yk),假设输出为 y ^ k = ( y ^ 1 k , y ^ 2 k , . . . , y ^ l k ) \hat{y}_k=(\hat{y}_1^k,\hat{y}_2^k,...,\hat{y}_l^k) y^k=(y^1k,y^2k,...,y^lk),即 y ^ j k = f ( β j − θ j ) \hat{y}_j^k=f(\beta_j-\theta_j) y^jk=f(βj−θj).
均方误差: E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac{1}{2}\displaystyle \sum_{j=1}^l(\hat{y}_j^k-y_j^k)^2 Ek=21j=1∑l(y^jk−yjk)2.
上层的网络中一共有 ( d + l + 1 ) q + l (d+l+1)q+l (d+l+1)q+l个参数要确定:
- 输入层到隐层: d × q d×q d×q
- 隐层到输入层: q × l q×l q×l
- 隐层神经元阈值: q q q
- 输出层神经元阈值: l l l
BP算法是一个迭代算法,在每一轮迭代中采用广义的感知机学习规则对参数进行估计更新,对任意参数 v v v的更新估计式为: v ← v + Δ v v \leftarrow v+\Delta v v←v+Δv.
下面以隐层到输出层的连接权$\omega_{hj}为例。
BP 算法基于梯度下降(gradient descent) 策略, 以目标的负梯度方向对参数进行调整,对 E K E_K EK,给定学习率 η \eta η,有: Δ ω h j = − η ∂ E k ∂ ω h j \Delta\omega_{hj}=-\eta\frac{\partial E_k}{\partial\omega_{hj}} Δωhj=−η∂ωhj∂Ek.
由链式法则:
∂
E
k
∂
ω
h
j
=
∂
E
k
∂
y
^
j
k
⋅
∂
y
^
j
k
∂
β
j
⋅
∂
β
j
∂
ω
h
j
\frac{\partial E_k}{\partial\omega_{hj}}=\frac{\partial E_k}{\partial\hat{y}_j^k}·\frac{\partial{\hat{y}_j^k}}{\partial\beta_j}·\frac{\partial\beta_j}{\partial\omega_{hj}}
∂ωhj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂ωhj∂βj,
ω
h
j
\omega_{hj}
ωhj会先影响第
j
j
j个输出层神经元的输入值,再影响其输出值
y
^
j
k
\hat{y}_j^k
y^jk,再影响到
E
k
E_k
Ek.’

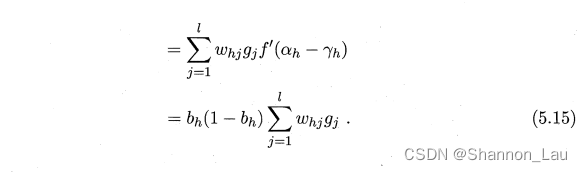
























 205
205











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








