svm系列之核函数+软边界

软边界svm一般形式

前面Hard-Margin svm 的一个缺点就是 会产生过拟合现象。特别是当使用核函数或者对偶的svm的时候，如果要求必须把数据点都区分的话，就会很任意发生过拟合现象。
由于有的数据是有噪声的，可能还是离群点，如果一定要求所有的点都必须分对的话，即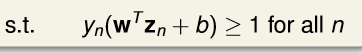 ，那么就有可能把误差带进去。所以我们想的是，把条件放宽一些，对于个别点，错就错了，没必要太追究。
我们原来的Hard-Margin svm表达形式为

我们借鉴pocket的表达式，就是错一点没什么，但是不要太多。则我们可以转化为

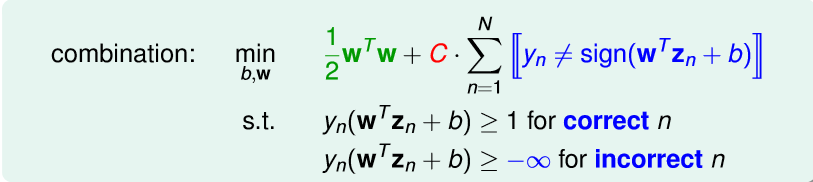
其中C是用来权衡 是要边界大，还是要误差容忍度大。
可将上式化简为

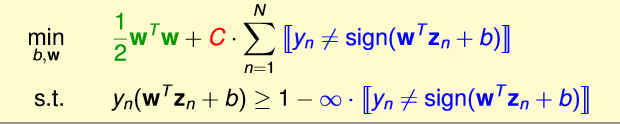
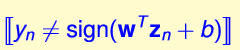
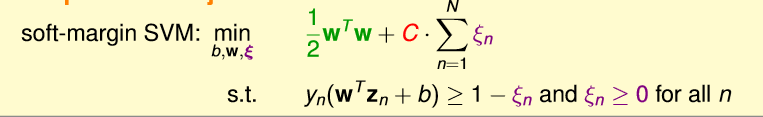
可是，对于这样形式的式子，他不是二次规划的形式。同时，我们不能区分最小误差和最大误差。也就是，有的数据点错的很远，非常远离分割线，可是我们给的误差处罚值为1，有的数据点错的很小，就在分割线旁边，可是我们给的误差处罚值依然为1。这就不好了。基于以上两个问题，我们决定将表达式进行修正。

这样就很好的处理了问题，原因是

其中$\varepsilon_n$紫色线部分violation

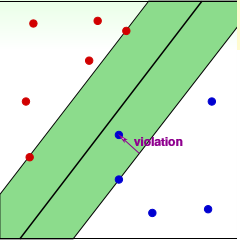
其中C是用来权衡 是要边界大，还是要误差容忍度大。
C越大，误差容忍度就越小，要求的边界越大，就可能会过拟合。
C越小，误差容忍度就越大，要求的边界越小，就可能会欠拟合。

软边界svm的对偶式

我们得到软边界svm的基本形式，现在用之前的步骤将其转化对偶形式。
具体步骤



最终结果为

软边界svm的kernel函数

与之前的类似，就是b的求解可能有点问题。
Hard margin svm 的b的求解为

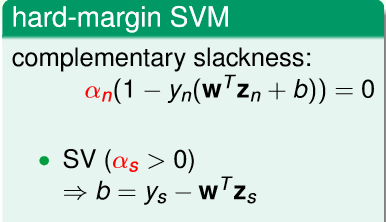
而现在的b的求解为

即不仅仅要求$\alpha_n<0$,还要求$\alpha_n>=0$
即最终有

其实即使这样，依然会导致一定程度的过拟合，所以要小心的调节参数。
$\alpha_n$的物理意义
其实$\alpha_n$的取值范围，可以反应出其对应点所处的位置。

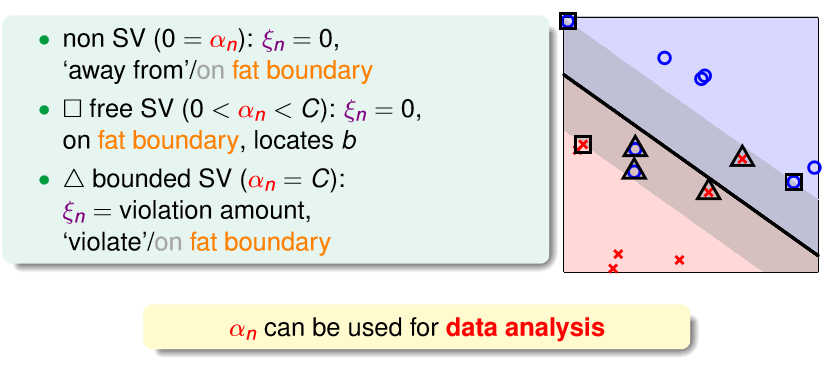
最后，
我们通过交叉验证的方法选择参数，要记住

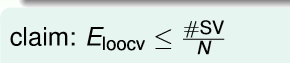
不过他仅仅是上限，不是很精确，只是在运算量很大时，近似估计一下。