Marioの《计算机程序设计艺术》读书笔记：数学归纳法

本期内容：卷一第一章 1.2.1 数学归纳法

本节内容先以一个命题谈起：

令P(n)是关于整数n的某个命题，假定我们需要证明P(n)对于所有正整数n为真，一种重要的做法是：（a）证明P(1)为真    （b）证明“如果P(1),P(2),P(3),···,P(n)全部为真，那么P(n+1)也为真”，这个证明对于任意正整数n成立。

文章先以一下等式序列举例（ 下称P(n) ）：

·····

（1）

（1）

(a) " 因为1=1^2，所以P(1)为真 "

(b) " 如果P(1),P(2),P(3),···,P(n)全部为真，特别的是P(n)为真，那么P(n+1)也为真，于是有式（1）成立，对其两端加上2n+1，得到

由此证明，P(n+1)也为真 "

我们把这个方法称为算法式证明过程，对于确立的步骤(a)(b)，对于任意正整数n，下述算法都能产生P(n)为真的证明。

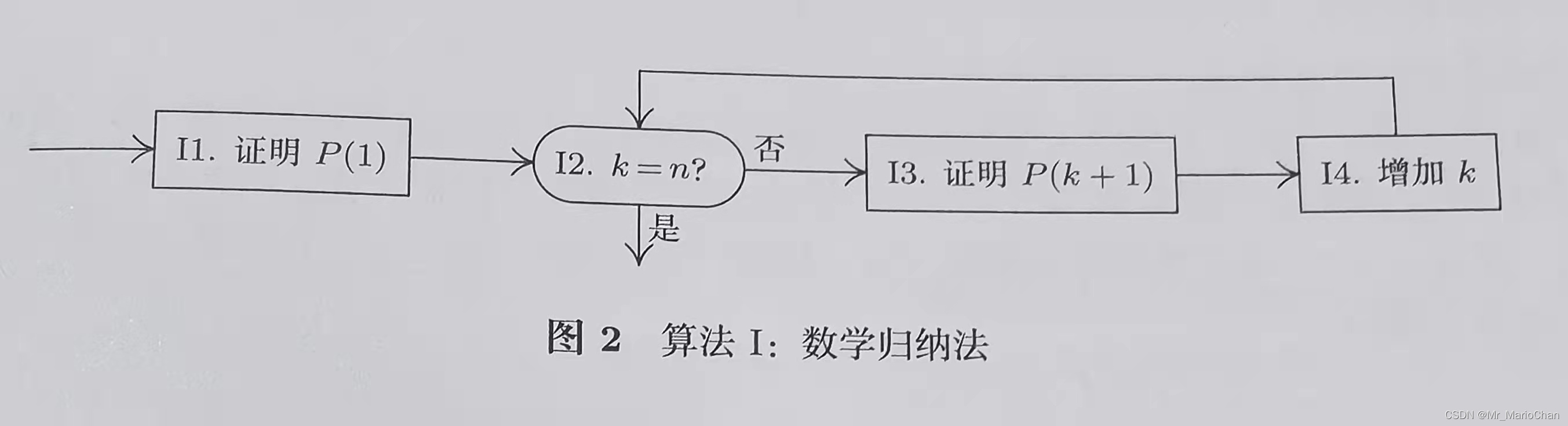
算法I（构造证明）

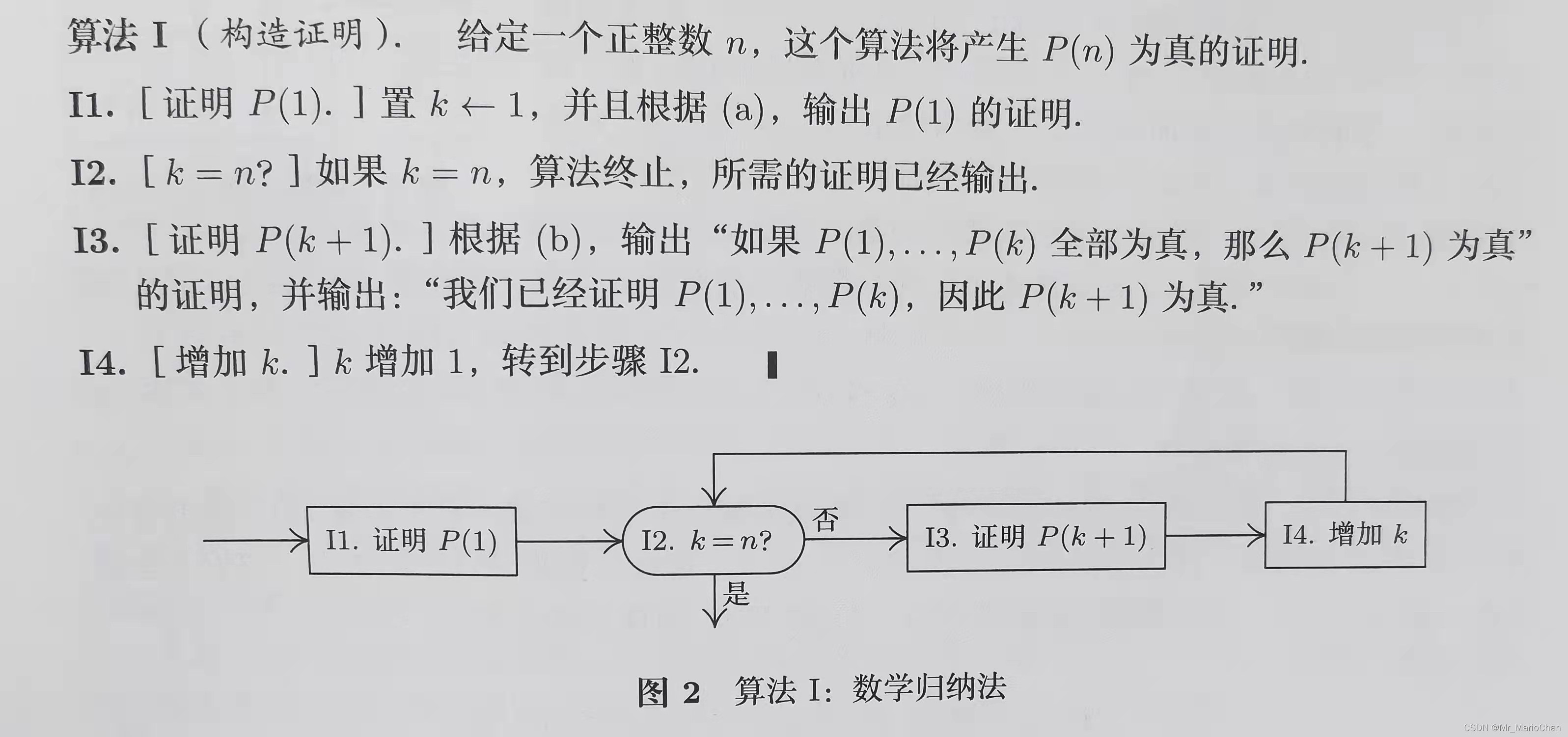
 可以理解为是一种已知到未知的合法推进，这种证明方法就是数学归纳法证明。

数学归纳法不同于科学归纳：科学归纳更多的是基于经验结果或者猜想下的对于情况的最佳猜测，而数学归纳法是对命题的确定性证明。

书中归纳的数学归纳法的一般步骤：

算法E（扩展欧几里得）

数学归纳法对于扩展欧几里得算法正确性的证明：

扩展欧几里得算法：给定两个正整数m和n，计算它们的最大公因数d，并计算两个未必为正数的正数a和b，使得am+bn=d. 

给定一下命题（1）：

如果指向某方框的至少一个箭头上的断言在执行方框内操作之前都为真，那么离开该方框的相关箭头上的所有断言在执行方框内操作之后都为真.

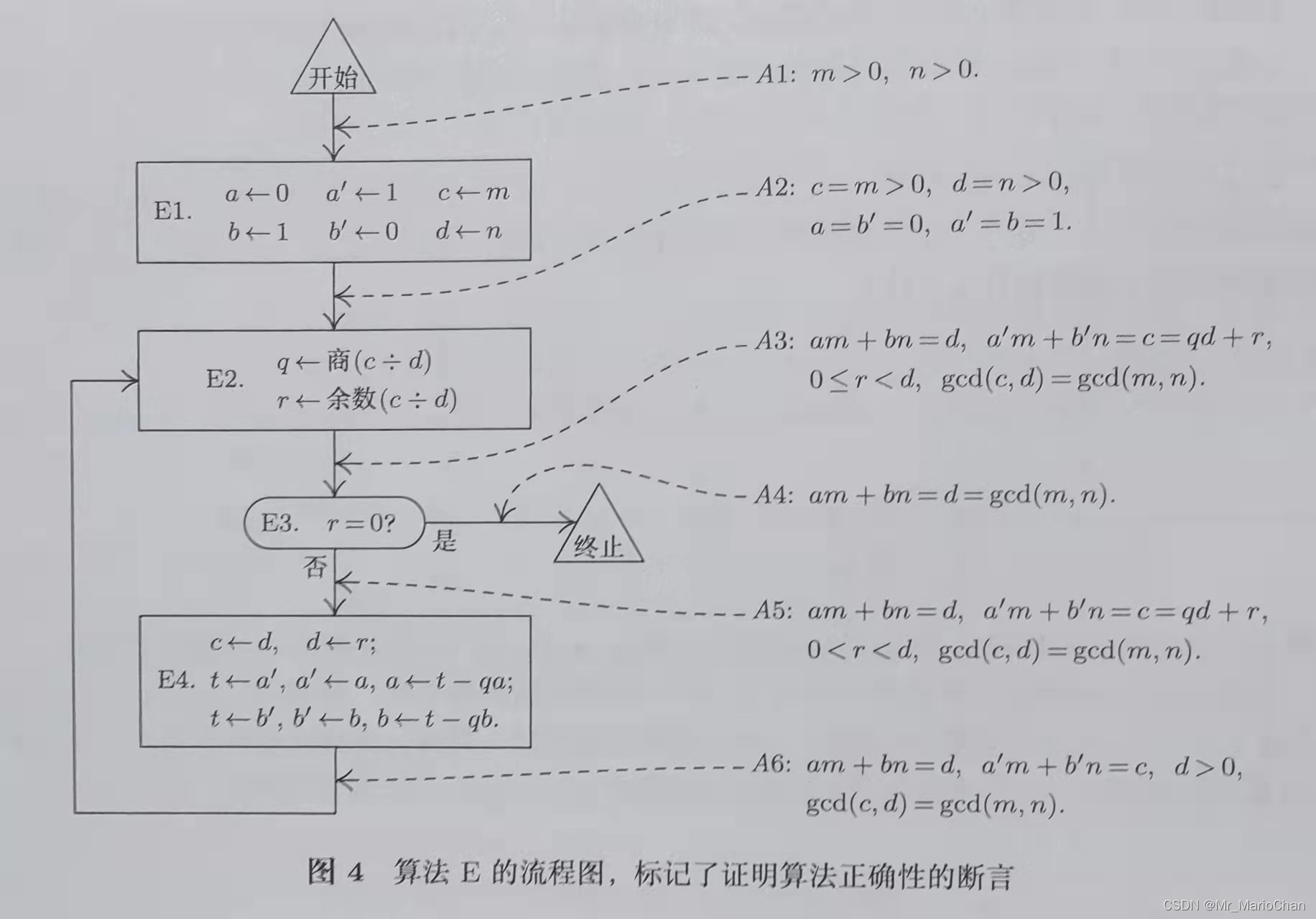
 以上为扩展欧几里得算法的流程图，一旦对每个方框都证明了命题（1），就可以推出在算法执行期间，所有断言都为真。

同时，为了使得这一过程满足算法的有穷性（有限性），还需单独证明算法会终止。

历史上，归纳断言概念的原始形态出现于1946年（以“断言框”的形式出现）

总结：对于数学归纳法，书中对于其方法分成两步，其第二步是满足已知P(1->n)的正确性，可以推出P(n+1)，这个是已知到位置的过程，对于第一个已知，即P(1)需要成立，这也就是第一步，两者逻辑联系紧密，缺一不可。依旧是晦涩难懂的一小节......