POJ_2411_Mondriaan's Dream

最新推荐文章于 2022-03-24 21:58:01 发布

Southan97

最新推荐文章于 2022-03-24 21:58:01 发布

阅读量437

点赞数

分类专栏： Dynamic Programming 文章标签： POJ 状压dp

本文链接：https://blog.csdn.net/Mrx_Nh/article/details/52080237

版权

Dynamic Programming 专栏收录该内容

9 篇文章 0 订阅

订阅专栏

Mondriaan's Dream

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 15097		Accepted: 8710

Description

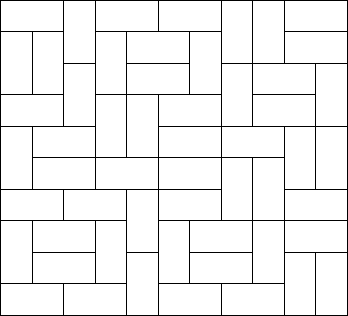
Squares and rectangles fascinated the famous Dutch painter Piet Mondriaan. One night, after producing the drawings in his 'toilet series' (where he had to use his toilet paper to draw on, for all of his paper was filled with squares and rectangles), he dreamt of filling a large rectangle with small rectangles of width 2 and height 1 in varying ways.

Expert as he was in this material, he saw at a glance that he'll need a computer to calculate the number of ways to fill the large rectangle whose dimensions were integer values, as well. Help him, so that his dream won't turn into a nightmare!

Input

The input contains several test cases. Each test case is made up of two integer numbers: the height h and the width w of the large rectangle. Input is terminated by h=w=0. Otherwise, 1<=h,w<=11.

output

For each test case, output the number of different ways the given rectangle can be filled with small rectangles of size 2 times 1. Assume the given large rectangle is oriented, i.e. count symmetrical tilings multiple times.

Sample Input

Sample Output

Source

Ulm Local 2000

题目的意思就是用1*2的小矩形去填满n*m的大矩形，求所有可能的填法。

乍看之下并无规律可循，但是我们若将n*m的矩形看成n*m个1*1的小正方形，细细分析可以发现，每一行摆放小矩形的状态既受上一行的影响，又会影响下一行，这里就要用到状态压缩dp的思想，由于必须把矩形填满，所以往下填的时候不能随意横竖放，譬如第i行就是最后一行，于是该行某一列就不能竖着往下放，会“超出下边界”，于是考虑往上填充，即i-i行的这一列是空着的，这样一来，第i行竖着往上填充补满i-1行并且第i行也填满了。用0表示第i-1行第j列没有放置矩形，1表示放了矩形（这里其实表示的是1*1的小正方形，我们用连续两个1表示横放一个小矩形）。那么到第i行将第i-1行取反，0就变成1就是在该列竖着往上填充，1变成0，到这里，问题的关键来了，第i-1行某列竖着放是1，横着放也是1，取反后第i行该列就是0，然而只有第i-1行是横着放时我们才能放，否则就已经“小正方形”被填充了，又因为上面说到我们是要在填满第i行的同时补满第i-1行，取反后自然补满了第i-1行，所以我们只要考虑由第i行所有横着放的可能并加上第i-1行所有发出状态就解决了。

注意dp要用long long或者__int64

/**********************************************

状压dp

欢迎交流！

还请各位不吝赐教！

***********************************************/

#include <iostream>
#include <iomanip>
#include <cstring>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <set>
#include <map>
#include <list>
#include <stack>
#include <deque>
#include <queue>
#include <vector>
#include <algorithm>
#include <functional>

#define PI acos(-1.0)
#define eps 1e-10
#define INF 0x7fffffff
#define MOD 1000000007
#define debug(x) cout << "--------------> " << x << endl

typedef __int64 ll;
typedef long long LL;
typedef unsigned long long ULL;

using namespace std;

int n, m;
ll dp[14][1 << 11], tmp;                   //dp[i][j]表示前i行在前i行j种状态下符合条件的方案数
void dfs(int i, int p, int j)              //找第i行，在第i-1行状态为p时，第j列的所有横放可能
{
        if (j >= m)
        {
                dp[i][p] += tmp;
                return ;
        }
        dfs(i, p, j + 1);
        if (j <= m - 2 && !(p & (1 << j)) && !(p & (1 << j + 1)))       //第i-1行的状态p在第m-j-1和第m-j-2列为0，即没有摆放
        {
                dfs(i, p | (1 << j) | (1 << (j + 1)), j + 2);           //在第m-j-1和第m-j-2列可以可以横放一个矩形，列从0到m-1
        }
}

int main()
{
        while (scanf("%d%d", &n, &m), n + m)
        {
                memset(dp, 0, sizeof(dp));
                tmp = 1;
                dfs(1, 0, 0);
                for (int i = 2; i <= n; ++i)
                {
                        for (int j = 0; j < (1 << m); ++j)               //每一行共1<<m种状态，行从1开始计数，列从0开始计数
                        {
                                if (dp[i - 1][j])
                                tmp = dp[i - 1][j];
                                else                                     //由第i-1行发出的状态不能使第i行以满足条件的方式填充
                                continue;
                                dfs(i, ~j & ((1 << m) - 1), 0);
                        }
                }
                printf("%I64d\n", dp[n][(1 << m) - 1]);
        }
        return 0;
}