ABC342 A-G

Muelsyse_

已于 2024-02-25 17:18:44 修改

阅读量819

点赞数 17

分类专栏： Atcoder 文章标签：算法

于 2024-02-25 17:12:56 首次发布

本文链接：https://blog.csdn.net/Muelsyse_/article/details/136282494

版权

Atcoder 专栏收录该内容

21 篇文章 3 订阅

订阅专栏

HUAWEI Programming Contest 2024（AtCoder Beginner Contest 342） - AtCoder

被薄纱的一场

A - Yay!

题意：

给出一串仅由两种小写字母构成的字符串，其中一种小写字母仅出现一次，输出那个仅出现一次的小写字母的位置

代码：

STL偷懒了（）

char ch[N];
map<char, vector<int>>mp;
void solve()
{
    scanf("%s", ch + 1);
    for (int i = 1; ch[i]; ++i)
        mp[ch[i]].push_back(i);
    auto it = mp.begin();
    if (it->second.size() == 1)
    {
        printf("%d\n", it->second.back());
        return;
    }
    it = mp.end(); --it;
    printf("%d\n", it->second.back());
    return;
}

B - Which is ahead?

题意：

N个人排队，排在第i个位置的人的编号是Pi，给出Q组询问，每组询问输出编号分别为 x 和 y 的人谁在前面

题解：

存下每个人的位置然后查询时直接比较即可

map<int, int>mp;//其实可以直接用数组
void solve()
{
    int n;
    scanf("%d", &n);
    for (int i = 1, x; i <= n; ++i)
    {
        scanf("%d", &x);
        mp[x] = i;
    }
    int q;
    scanf("%d", &q);
    while (q--)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        if (mp[a] < mp[b])
            printf("%d\n", a);
        else
            printf("%d\n", b);
    }
}

C - Many Replacement

题意：

给出一串长度为N的由小写字母构成的字符串和Q次操作，每次操作表示将字符串中的所有ci字符变为di字符，输出经过所有操作之后的字符串

题解：

f[26]记录每种字符经过操作之后变为了什么字符，O(26 * N)就能得出最后每种原本的字符最终会变为哪种字符，具体做法见代码

char ch[N];
int f[26];
void solve()
{
    for (int i = 0; i < 26; ++i)
        f[i] = i;
    int n;
    scanf("%d%s", &n, ch + 1);
    int q;
    scanf("%d", &q);
    while (q--)
    {
        char a, b;
        scanf(" %c %c", &a, &b);
        for (int i = 0; i < 26; ++i)
        {
            if (f[i] == a - 'a')
                f[i] = b - 'a';
        }
    }
    for (int i = 1; i <= n; ++i)
        printf("%c", f[ch[i] - 'a'] + 'a');
}

D - Square Pair

题意：

给出一个长度为N的数组A，求数对(i, j)满足i < j, Ai*Aj 是平方数的数对数量

题解：

Ai<=2e5，可以用桶来存下所有的数据，并且我们可以枚举所有平方数（0*0, 1*1, ... , 2e5*2e5）。假设我们要求乘积是 x * x 的数对的数量，首先特判一下Ai = Aj = x的情况（具体见代码），其次对于Ai != Aj的情况，我们可以通过求x * x的所有小于x的因数 t， $\sum cnt[t]*cnt[x*x/t]$ 就是Ai != Aj时的数对数量

对于求x * x的因数显然我们不能直接O(sqrt(x*x))求，由于平方数的性质，我们可以先求出x的因数，然后x的因数与x的因数两两相乘就能求出x * x的因数（总体时间复杂度不太好证，反正这种做法跑了600ms）

最后对于Ai * Aj = 0也需要特判一下

const LL N = 2e5 + 10;
LL a[N], cnt[N];
vector<LL>v[N];
void solve()
{
    for (int i = 1; i < N; ++i)//nlogn预处理1到N-1所有数的因数
    {
        for (int j = i; j < N; j += i)
            v[j].push_back(i);
    }
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i)
        scanf("%lld", &a[i]), ++cnt[a[i]];
    LL ans = cnt[0] * (cnt[0] - 1) / 2 + cnt[0] * (n - cnt[0]);//特判乘积为0
    for (int i = 1; i < N; ++i)
    {
        ans += cnt[i] * (cnt[i] - 1) / 2;//特判Ai = Aj
        vector<LL>t;
        for (int j = 0; j < v[i].size(); ++j)//求x * x的因数
        {
            for (int k = j; k < v[i].size() && v[i][j] * v[i][k] < i; ++k)
                t.push_back(v[i][j] * v[i][k]);
        }
        sort(t.begin(), t.end());
        t.erase(unique(t.begin(), t.end()), t.end());//去重
        for (auto j : t)
        {
            LL k = (LL)i * i / j;
            if (k < N)ans += cnt[j] * cnt[k];
        }
    }
    printf("%lld\n", ans);
}

E - Last Train

题意：

有一座城市中有N个公交站台，共有M种公交线路(li, di, ki, ci, Ai, Bi) 表示从 li 时刻开始，每 di 单位时间会有一辆公交车从 Ai 出发，经过 ci 时间到达 Bi 站台，并且这种线路总计发车ki辆，在发出第ki辆公交车后不再发车（末班车在 li + (ki - 1) * di 时刻发出）

设f(x)是从x站台出发，最终能够到达站台n的最晚出发时间，求f(1), f(2), ... ,f(n - 1)，不能到达输出Unreachable

题解：

假设从Bi站台出发，最终能到达站台n的最晚出发时间是 x ，同时我们有一条公交线路(li, di, ki, ci, Ai, Bi)，显然我们可以通过Bi的最晚出发时间x，来更新Ai的最晚出发时间

所以我们可以建反边，跑dijkstra，初始化ans[n] = INF（至少要大于1e18+1e9），其他的ans值为负值

struct edge
{
    LL v, l, d, k, c;
};
LL ans[N];
vector<edge>e[N];
void solve()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i)
        ans[i] = -1;
    for (int i = 1; i <= m; ++i)
    {
        int l, d, k, c, a, b;
        scanf("%d%d%d%d%d%d", &l, &d, &k, &c, &a, &b);
        e[b].push_back({ a,l,d,k,c });
    }
    ans[n] = 2e18;
    priority_queue<PLL>q;
    q.push({ ans[n],n });
    while (q.size())
    {
        LL u = q.top().second, wu = q.top().first; q.pop();
        if (wu < ans[u])
            continue;
        for (auto& it : e[u])
        {
            LL v = it.v, l = it.l, d = it.d, k = it.k, c = it.c;
            LL mxt = wu - c;
            if (mxt < l)continue;
            LL step = (mxt - l) / d;
            step = min(step, k - 1);
            LL res = l + step * d;//通过u更新的v的最晚出发时间
            if (res > ans[v])
            {
                ans[v] = res;
                q.push({ res,v });
            }
        }
    }
    for (int i = 1; i < n; ++i)
    {
        if (ans[i] > 0)printf("%lld\n", ans[i]);
        else printf("Unreachable\n");
    }
}

F - Black Jack

题意：

你与对手玩这样的一个游戏：游戏使用一个D面骰子能等概率得骰出1到D之间的任意整数，并且有两个初始为0的整数 x 和 y。

刚开始由你先开始投掷，你可以投掷骰子任意次，在每次投掷之后你将这次骰出的点数加到x上，并且选择是否继续投掷。

接下来由你的对手开始投掷，若y<l，则他进行一次投掷，并将骰出的点数加到y上，直到y>=l。

在完成所有投掷后，若x>n，判定为你输了；若x>y或y>n，判定为你赢了；其他情况均判定为你输了，求在你进行最优决策的情况下你的胜率。

题解：

显然对方是做不了决策的，对方最终y为每种值的概率都是确定的，设b[i]为y最终为i的概率

而我方可以做出如下决策：在x <= t时选择继续投掷，直到x > t。对每种决策都可以确定最终x为每种值的概率，设a[i]为x最终为i的概率，同时设f为x <= n的概率，最终答案为 $\sum_{i=1}^{n}(a[i]* \sum_{j=1}^{i-1}b[j])+f*(1- \sum_{j=1}^{n}b[j])$ ，这里可以b[i]数组进行前缀和优化；对于x <= t+1时继续投掷最终的a[i]可以通过x <= t时继续投掷的a[i]求得，转移是a[i] += a[t] / d,(t < i <= min(n, t + d)) , a[t] = 0，f -= a[t] - a[t] / d * (min(n, t + d) - t)这样最终的时间复杂度是O(N^2)，显然还不可做。

对于a[i] += a[t] / d,(t < i <= min(n, t + d))的区间赋值操作我们可以通过差分数组优化掉，而对于确定t时的胜率我们是否也能通过O(1)转移到t + 1，设在t时的胜率为ans， $s[i]=\sum_{j=1}^{i}b[i]$ ，则a[t] = 0操作损失的胜率为ans -= a[t] * s[i - 1]，而对于a[i] += a[t] / d,(t < i <= min(n, t + d)) ，增加的胜率为 $ans+=\sum_{j=t+1}^{min(n, t + d)}(a[t]/d*s[j-1])$ ，提出a[t]/d，对于 $\sum s[j-1]$ 显然我们也可以前缀和优化掉，这样就完成了O(1)转移，最后处理一下j - 1的边界问题即可，时间复杂度O(N)

double a[N], b[N], dt[N], ad, s[N], ss[N];//dt[]与ad为差分数组与∑dt[]
void solve()
{
    int n, l, d;
    scanf("%d%d%d", &n, &l, &d);
    a[0] = b[0] = 1;
    for (int i = 0; i < l; ++i)
    {
        ad += dt[i];
        b[i] += ad;
        dt[i + 1] += b[i] / d;
        if (i + d < n)dt[i + d + 1] -= b[i] / d;
        b[i] = 0;
    }
    for (int i = l; i <= n; ++i)
        ad += dt[i], b[i] += ad;
    for (int i = l; i <= n; ++i)
        s[i] = s[i - 1] + b[i];
    for (int i = l; i <= n; ++i)
        ss[i] = ss[i - 1] + s[i];
    double ans = 0, t = 0, f = 1;
    memset(dt, 0, sizeof dt);
    ad = 0;
    for (int i = 0; i < n; ++i)//当x<=i时继续投掷的决策
    {
        ad += dt[i];
        a[i] += ad;
        dt[i + 1] += a[i] / d;
        if (i + d < n)dt[i + d + 1] -= a[i] / d;
        int r = min(n, i + d);
        f -= (d - r + i) * a[i] / d;
        t += (ss[r - 1] - (i ? ss[i - 1] : 0)) * a[i] / d;
        if (i)t -= a[i] * s[i - 1];
        ans = max(ans, t + f * (1 - s[n]));
    }
    printf("%.10lf", ans);
}

G - Retroactive Range Chmax

题意：

给出一个长度为N的数组A，对该数组进行Q次操作，操作分为三种：

1 l r x：对所有l, r范围内的数与x取最大值 Ai = max(Ai, x), l <= i <= r

2 i：撤销第i步操作（题目保证第i步操作时1操作并且未被撤销过）

3 i：查询Ai的值

题解：

首先我们不直接对A数组进行操作，可以用类似于线段树的结构来存储修改操作，一棵线段树的结构大致是这样：

假设我们要对区间(3, 7)进行赋值，我们仅需在这些节点放入x

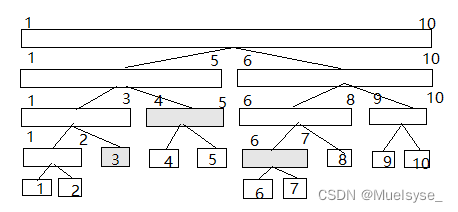
同理若对(2, 5)赋值，我们仅需在这些节点放入x

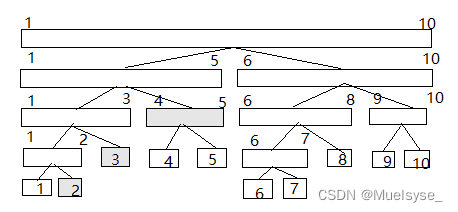
可以证明最多在2*logn个节点放入x

对于撤销修改操作，我们可以用4*N个multiset来作为线段树的节点，在每次1操作时在对应节点放入x，在每次2操作时在对应节点删除x即可

然后在查询操作时查询i上方的所有节点的最大值，并与Ai取max即可（或者直接在线段树的子节点放入他们原本的值也行），为了不re可以在每个节点都提前塞个0进去

因为用到了线段树+multiset时间复杂度大概在O(q*logn*logn)，并且还有点常数跑了2s，但题目给了5s时限，还是嘎嘎过的

int a[N], ql[N], qr[N], x[N];
multiset<int>tr[N << 2];
void updata(int pos, int l, int r, int i)
{
    if (ql[pos] <= l && r <= qr[pos])
    {
        tr[i].insert(x[pos]);
        return;
    }
    int mid = l + r >> 1;
    if (ql[pos] <= mid)updata(pos, l, mid, i << 1);
    if (qr[pos] > mid)updata(pos, mid + 1, r, i << 1 | 1);
}
void erase(int pos, int l, int r, int i)
{
    if (ql[pos] <= l && r <= qr[pos])
    {
        tr[i].erase(tr[i].find(x[pos]));
        return;
    }
    int mid = l + r >> 1;
    if (ql[pos] <= mid)erase(pos, l, mid, i << 1);
    if (qr[pos] > mid)erase(pos, mid + 1, r, i << 1 | 1);
}
int query(int pos, int l, int r, int i)
{
    if (l == r)
        return *tr[i].rbegin();
    int mid = l + r >> 1, res = *tr[i].rbegin();
    if (pos <= mid)res = max(res, query(pos, l, mid, i << 1));
    else res = max(res, query(pos, mid + 1, r, i << 1 | 1));
    return res;
}
void solve()
{
    int n;
    scanf("%d", &n);
    for (int i = 1; i <= n << 2; ++i)
        tr[i].insert(0);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &a[i]);
    int q;
    scanf("%d", &q);
    for (int i = 1; i <= q; ++i)
    {
        int op, pos;
        scanf("%d", &op);
        if (op == 1)
        {
            scanf("%d%d%d", &ql[i], &qr[i], &x[i]);
            updata(i, 1, n, 1);
        }
        else if (op == 2)
        {
            scanf("%d", &pos);
            erase(pos, 1, n, 1);
        }
        else
        {
            scanf("%d", &pos);
            printf("%d\n", max(a[pos], query(pos, 1, n, 1)));
        }
    }
}