在多元线性回归模型经典假设中,其重要假定之一是回归模型的解释变量之间不存在线性关系,也就是说,解释变量X1,X2,……,Xk中的任何一个都不能是其他解释变量的线性组合。如果违背这一假定,即线性回归模型中某一个解释变量与其他解释变量间存在线性关系,就称线性回归模型中存在多重共线性。多重共线性违背了解释变量间不相关的古典假设,将给普通最小二乘法带来严重后果。
所谓多重共线性是指线性回归模型的解释变量之间由于存在精确相关关系或者高度相关关系而使模型评估失真或者不准确。这里,我们总结了8个处理多重共线性问题的可用方法,大家在遇到多重共线性问题时可作参考:
1、保留重要解释变量,去掉次要或可替代解释变量
自变量之间存在共线性,说明自变量所提供的信息是重叠的,可以删除不重要的自变量减少重复信息。但从模型中删去自变量时应该注意:从实际经济分析确定为相对不重要并从偏相关系数检验证实为共线性原因的那些变量中删除。如果删除不当,会产生模型设定误差,造成参数估计严重有偏的后果。
2、改变解释变量的形式
改变解释变量的形式是解决多重共线性的一种简易方法,例如对于横截面数据采用相对数变量,对于时间序列数据采用增量型变量。
3、差分法
4、逐步回归分析
逐步回归(Stepwise Regression)是一种常用的消除多重共线性、选取“最优”回归方程的方法。其做法是将逐个引入自变量,引入的条件是该自变量经F检验是显著的,每引入一个自变量后,对已选入的变量进行逐个检验,如果原来引入的变量由于后面变量的引入而变得不再显著,那么就将其剔除。引入一个变量或从回归方程中剔除一个变量,为逐步回归的一步,每一步都要进行F 检验,以确保每次引入新变量之前回归方程中只包含显著的变量。这个过程反复进行,直到既没有不显著的自变量选入回归方程,也没有显著自变量从回归方程中剔除为止。
5、主成份分析
主成分分析作为多元统计分析的一种常用方法在处理多变量问题时具有其一定的优越性,其降维的优势是明显的,主成分回归方法对于一般的多重共线性问题还是适用的,尤其是对共线性较强的变量之间。
6、偏最小二乘回归
7、岭回归
岭回归估计是通过最小二乘法的改进允许回归系数的有偏估计量存在而补救多重共线性的方法,采用它可以通过允许小的误差而换取高于无偏估计量的精度, 因此它接近真实值的可能性较大。灵活运用岭回归法, 可以对分析各变量之间的作用和关系带来独特而有效的帮助。
8、增加样本容量
多重共线性问题的实质是样本信息的不充分而导致模型参数的不能精确估计,因此追加样本信息是解决该问题的一条有效途径。但是,由于资料收集及调查的困难,要追加样本信息在实践中有时并不容易。
这次我们主要研究逐步回归分析方法是如何处理多重共线性问题的。
逐步回归分析方法的基本思想是通过相关系数r、拟合优度R2和标准误差三个方面综合判断一系列回归方程的优劣,从而得到最优回归方程。具体方法分为两步:
对每一个回归方程进行统计检验分析(相关系数r、拟合优度R2和标准误差),并结合经济理论分析选出最优回归方程,也称为基本回归方程。
第二步,将其他解释变量逐一引入到基本回归方程中,建立一系列回归方程,根据每个新加的解释变量的标准差和复相关系数来考察其对每个回归系数的影响,一般根据如下标准进行分类判别:
1.如果新引进的解释变量使R2得到提高,而其他参数回归系数在统计上和经济理论上仍然合理,则认为这个新引入的变量对回归模型是有利的,可以作为解释变量予以保留。
2.如果新引进的解释变量对R2改进不明显,对其他回归系数也没有多大影响,则不必保留在回归模型中。
3.如果新引进的解释变量不仅改变了R2,而且对其他回归系数的数值或符号具有明显影响,则认为该解释变量为不利变量,引进后会使回归模型出现多重共线性问题。不利变量未必是多余的,如果它可能对被解释变量是不可缺少的,则不能简单舍弃,而是应研究改善模型的形式,寻找更符合实际的模型,重新进行估计。如果通过检验证明回归模型存在明显线性相关的两个解释变量中的其中一个可以被另一个很好地解释,则可略去其中对被解释变量影响较小的那个变量,模型中保留影响较大的那个变量。
下边我们通过实例来说明逐步回归分析方法在解决多重共线性问题上的具体应用过程。
具体实例
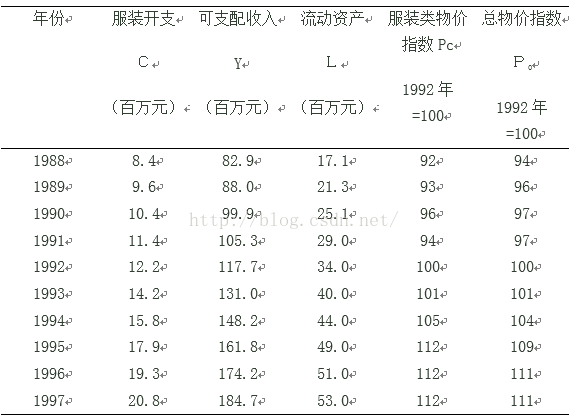
例1设某地10年间有关服装消费、可支配收入、流动资产、服装类物价指数、总物价指数的调查数据如表1,请建立需求函数模型。
表1 服装消费及相关变量调查数据
模型的检验量得分,R2=0.998,D·W=3.383,F=626.4634
R2接近1,说明该回归模型与原始数据拟合得很好。由得出拒绝零假设,认为服装支出与解释变量间存在显著关系。
上述基本相关系数表明解释变量间高度相关,也就是存在较严重的多重共线性。
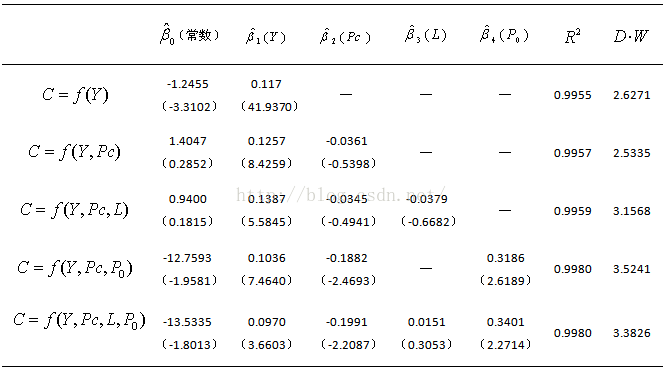
(3)为检验多重共线性的影响,作如下简单回归:
各方程下边括号内的数字分别表示的是对应解释变量系数的t检验值。
观察以上四个方程,根据经济理论和统计检验(t检验值=41.937最大,拟合优度也最高),收入Y是最重要的解释变量,从而得出最优简单回归方程。
表2 服装消费模型的估计
结果分析:
①在最优简单回归方程中引入变量Pc,使R2由0.9955提高到0.9957;根据经济理论分析,正号,负号是合理的。然而t检验不显著(),而从经济理论分析,Pc应该是重要因素。虽然Y与Pc高度相关,但并不影响收入Y回归系数的显著性和稳定性。依照第1条判别标准,Pc可能是“有利变量”,暂时给予保留。
②模型中引入变量L,R2由0.9957提高到0.9959,值略有提高。一方面,虽然Y与L,Pc与L均高度相关,但是L的引入对回归系数、的影响不大(其中的值由0.1257变为0.1387,值由-0.0361变为-0.0345,变化很小);另一方面,根据经济理论的分析,L与服装支出C之间应该是正相关关系,即的符号应该为正号而非负号,依照第2条判别标准,解释变量L不必保留在模型中。
③舍去变量L,加入变量P0,使R2由0.9957提高到0.9980,R2值改进较大。、、均显著(这三个回归系数的t检验值绝对值均大于),从经济意义上看也是合理的(服装支出C与Y,P0之间呈正相关,而与服装价格Pc之间呈负相关关系)。根据判别标准第1条,可以认为Pc、P0皆为“有利变量”,给予保留。
④最后再引入变量L,此时R2=0.9980没有增加(或几乎没有增加),新引入变量对其他三个解释变量的参数系数也没有产生多大影响,可以确定L是多余变量,根据判别标准第2条,解释变量L不必保留在模型中。
通过以上案例的分析,我们从理论和实际问题两方面具体了解了逐步回归分析是如何对多重共线性问题进行处理的。事实上,一般统计软件如SPSS,在回归模型的窗口中都会提供变量逐步进入的选项,勾选后实际上就是选择了运用逐步回归的思想来构建回归模型。运用SPSS软件不需要我们懂得其背后的运行规律,然而作为分析师,了解并理解模型背后的理论知识,将更有助于我们理解模型、解释结论背后的内在含义,从而达到更好地分析问题的目的。






















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








