线段树与树状数组基础及其应用

整体而言，线段树是包括树状数组的，即可以用树状数组解决的问题一般都能够用线段树解决，下面先介绍树状数组

一、树状数组相关概念解释

1.应用：

以O（logn）的复杂度快速求前缀和

2.主要操作：

（1）给某个位置上的数加上一个数

（2）求某一个前缀和

这两个操作都是以O（logn）的时间复杂度实现的，两个基本操作即单点修改，区间查询，其他的操作都是在这两个操作的基础上实现的，如区间修改，单点查询和区间修改和区间查询

3.基本原理，基本操作

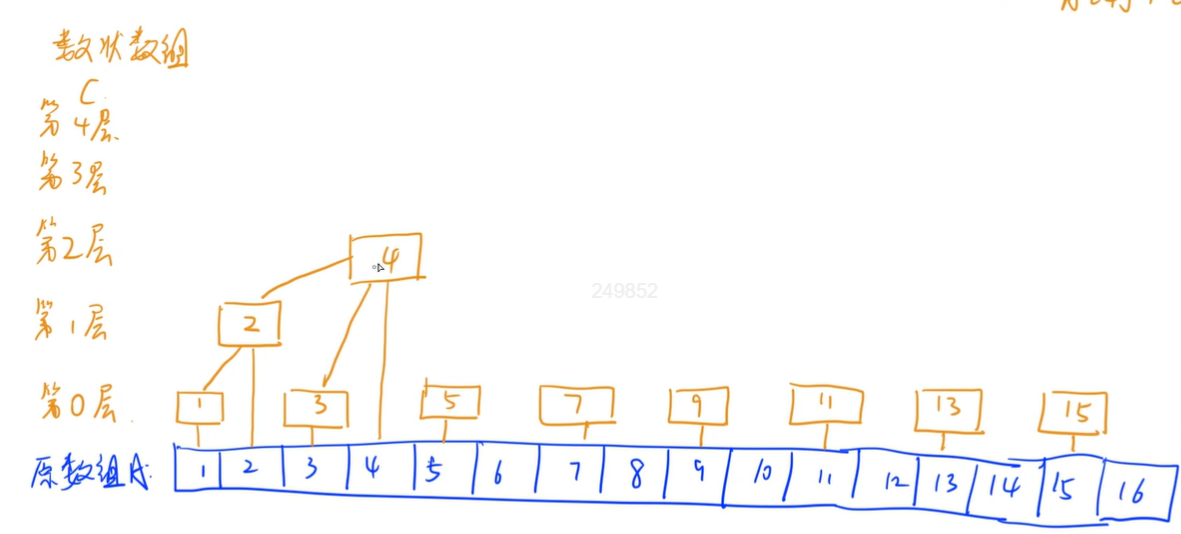
（1）首先定义一个数组A[]:

（2）再定义一个树状数组C[],在C中，所有奇数都和A数组相等，我们将其定义为第0层：

（3）再来定义第1层，第1层中的C[2]为A[1]+A[2]，而C[4]则在第三层，其值为C[4]=C[2]+C[3]+C[4],又因为C[2]=A[1]+A[2],故C[4]是前四项的和：

（4）依次地，可以画出整个树状数组的全貌：

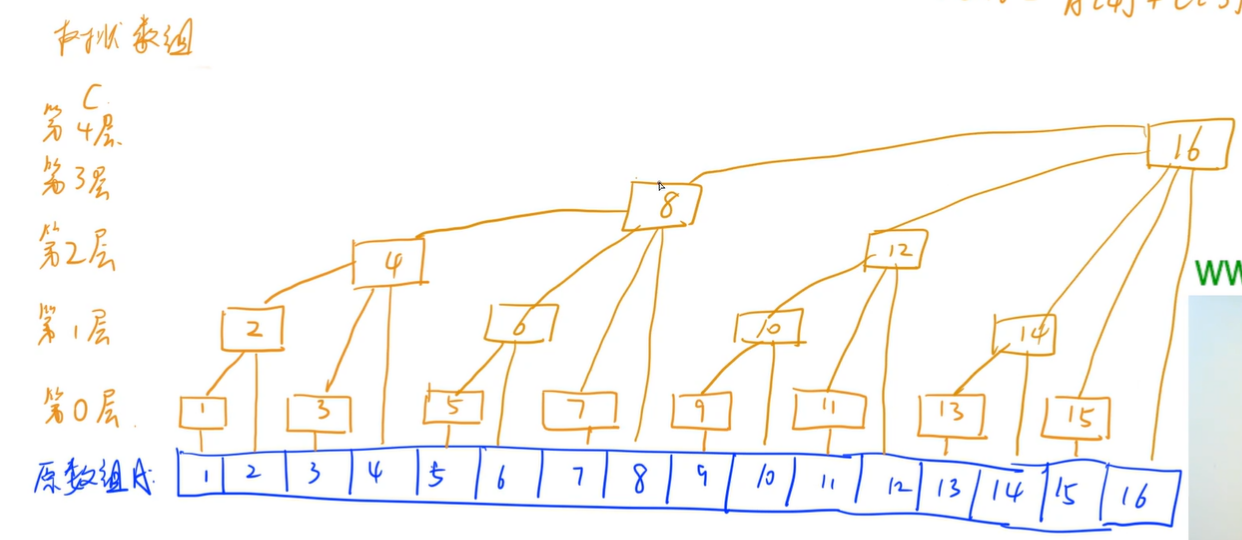
从这张图中可以发现以下几点：

a.某个数在第几层取决于它最多能够被2的几次方整除(也可以看成末尾有几个零就是第几层)

b.假设x的二进制表示有k个零，C[X]表示x-2^k到x之间A[I]的和，其中2^k可以表示为lowbit(x),

(lowbit(x)=x&-x)或(lowbit(x)=x&(x-1))

（5）当要求某个前缀和时，需要递归操作，例如，若求前X个数的和，即求x-2^k到x之间A[I]的和加上后面的，依次递归，便可写出如下函数：

int query(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

（6）进行更新操作时，只需要改动几个数就可以，例如改动第七个元素的值，则只需要改动7,8,16：

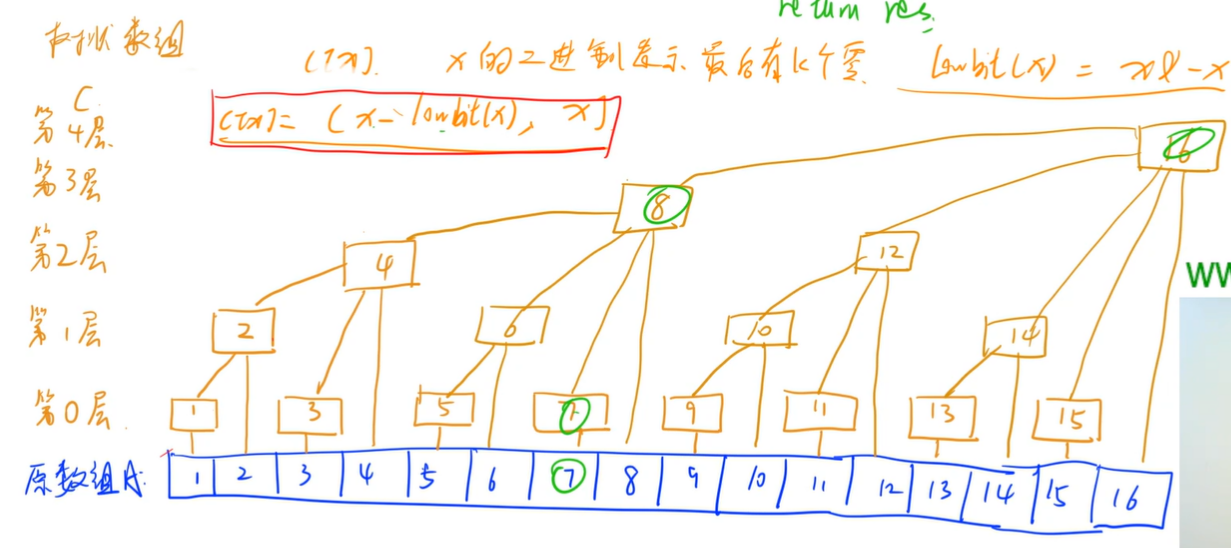
代码如下：

void add(int x, int v)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += v;
}

不难看出，树状数组的这两个操作（单点修改，区间查询）复杂度均为O(logn)

二、树状数组基础应用

1.下面介绍开头提到的两个基本操作即单点修改，区间查询

（1）单点修改有两种情况

a.加一个数v，即A[I]+v;

b.将这个数改成v,即A[I]+=（-A[I]）+ v ;

（2）求某个前缀和

求A[X]即C[X]-C[X-1]；

其他的和前缀和相同，A[L]-A[R-1]即可

#include<iostream>
#include<cstdio>
using namespace std;
int n,m;
int a[100010],tree[100010];
int lowbit(int x)
{
    return x&-x;
}
void add(int x,int v)
{
    for(int i=x;i<=n;i+=lowbit(i))tree[i]+=v;
}
int query(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))res+=tree[i];
    return res;
}
int  main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    for(int i=1;i<=n;i++)add(i,a[i]);
    while (m--)
    {
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        if (k == 0) printf("%d\n", query(y) - query(x - 1));
        else add(x, y);
    }
    return 0;
}

三、树状数组小结

小结：树状数组的三个核心代码即为

lowbit

int lowbit(int x)
{
    return x&-x;
}

add

void add(int x,int v)
{
    for(int i=x;i<=n;i+=lowbit(i))tree[i]+=v;
}

query

int query(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))res+=tree[i];
    return res;
}

四、线段树的相关概念解释

1. 线段树的应用：

以完全二叉树的结构，用于维护一个序列

2.具象解释

（1）以一个长度为7的序列解释：

线段树的每个根节点都是一个结构体

struct Node{
    int l,r;
    int sum;
}

这里以sum为例，根节点存放的是区间和

假设这个序列的七个数分别为1,2,3,4,5,6,7

则线段树的最后一个结点sum值为7 *（1+7）/ 2=28

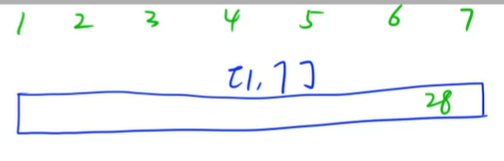
将上面的序列均分为两端，则得到[1,7]的两个儿子[1,4]和[5,7]

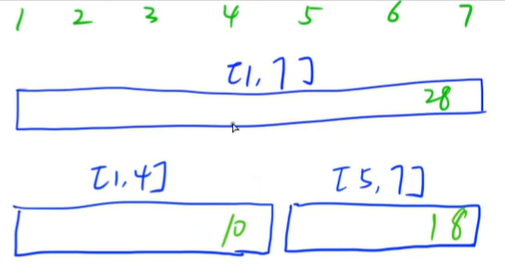
依次继续分下去

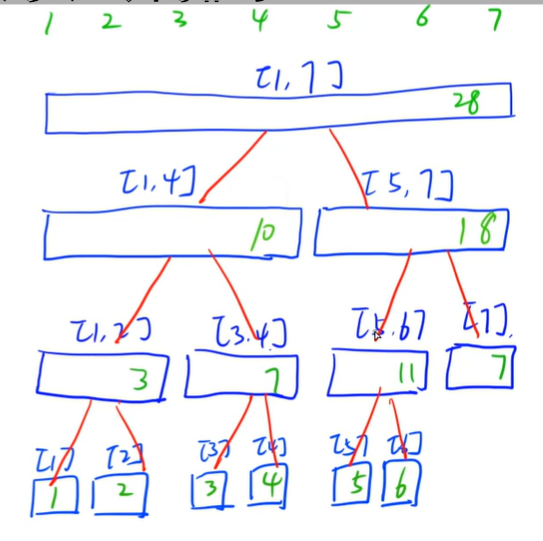
最后得到一个完全二叉树

3.核心操作

（1）操作一：单点修改modify

样例解释：若把上面序列中的5改为8

则只需要递归地改动线上的结点即可

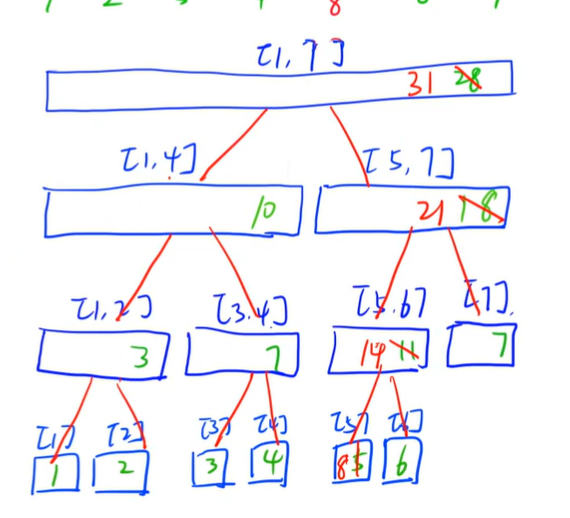
（2）操作二：区间查询query

假设要查询2-5上的和

检查此区间是否被覆盖，若覆盖，则直接加进去，否则递归寻找其儿子

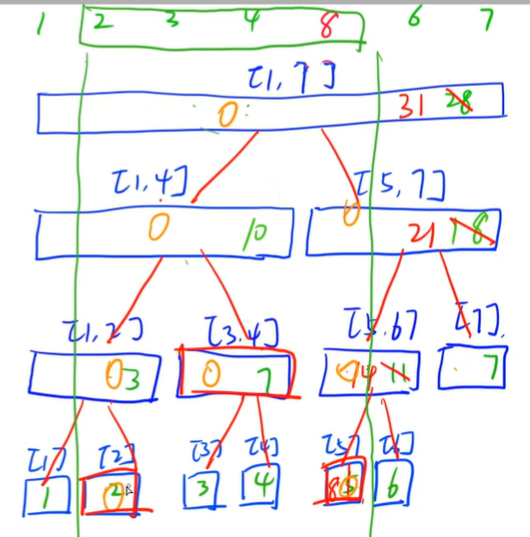
最终只有上图中的2,3-4,5三个区间被用到了，计算时间复杂度最高为O（logn）

4.核心函数

（1）pushup：用子结点信息来更新当前节点信息

void pushup(int u)
{
    tree[u].sum=tree[u<<1].sum+tree[u<<1|1].sum;
}

（2）build：在一段区间上初始化线段树

void build(int u,int l,int r)
{
    if(l==r)tree[u]={l,r,a[r]};
    else
    {
        tree[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid);
        build(u<<1|1,mid+1,r);
        pushup(u);
    }
}

（3）mulify：修改

void modify(int u,int x,int v)
{
    if(tree[u].l==tree[u].r)tree[u].sum+=v;
    else {
        int mid=tree[u].l+tree[u].r>>1;
        if(x<=mid)modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}

（4）query：查询区间和

int query(int u,int l,int r)
{
    if(tree[u].l>=l&&tree[u].r<=r)return tree[u].sum;
    int mid=tree[u].l+tree[u].r>>1;
    int sum=0;
    if(l<=mid)sum=query(u<<1,l,r);
    if(r>mid)sum+=query(u<<1|1,l,r);
    return sum;
}

2. 线段树的存储方式

如图，线段树的存储方式类似于堆

五、线段树基础应用

1.依然是上面那个题

总代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=100010;
int n,m;
int a[N];
struct Node{
    int l,r;
    int sum;
}tree[N*4];
void pushup(int u)
{
    tree[u].sum=tree[u<<1].sum+tree[u<<1|1].sum;
}
void build(int u,int l,int r)
{
    if(l==r)tree[u]={l,r,a[r]};
    else
    {
        tree[u]={l,r};
        int mid=l+r>>1;
        build(u<<1,l,mid);
        build(u<<1|1,mid+1,r);
        pushup(u);
    }
}
int query(int u,int l,int r)
{
    if(tree[u].l>=l&&tree[u].r<=r)return tree[u].sum;
    int mid=tree[u].l+tree[u].r>>1;
    int sum=0;
    if(l<=mid)sum=query(u<<1,l,r);
    if(r>mid)sum+=query(u<<1|1,l,r);
    return sum;
}
void modify(int u,int x,int v)
{
    if(tree[u].l==tree[u].r)tree[u].sum+=v;
    else {
        int mid=tree[u].l+tree[u].r>>1;
        if(x<=mid)modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    build(1,1,n);
    int k,a,b;
    while(m--)
    {
        scanf("%d%d%d",&k,&a,&b);
        if(k==0)printf("%d\n",query(1,a,b));
        else modify(1,a,b);
    }
    return 0;
}

2.其他应用：求数列区间最大值

只需要将刚才的sum运算改为max运算即可

总代码如下：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <climits>
using namespace std;
const int N = 100010;
int n, m;
int w[N];
struct Node
{
    int l, r;
    int maxv;
}tr[N * 4];
void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, w[r]};
    else
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        tr[u].maxv = max(tr[u << 1].maxv, tr[u << 1 | 1].maxv);
    }
}
int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].maxv;
    int mid = tr[u].l + tr[u].r >> 1;
    int maxv = INT_MIN;
    if (l <= mid) maxv = query(u << 1, l, r);
    if (r > mid) maxv = max(maxv, query(u << 1 | 1, l, r));
    return maxv;
}
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);

    build(1, 1, n);

    int l, r;
    while (m -- )
    {
        scanf("%d%d", &l, &r);
        printf("%d\n", query(1, l, r));
    }

    return 0;
}

六、小结

树状数组虽然代码短，但是应用限制多，使用情景少

而线段树虽然代码长，运行速度慢，但是可以应付掉大部分问题，包括可以用树状数组解决的题目