聚类分析
通常,人们可以凭借惊讶拟合专业知识来实现分类。而聚类分析(Cluster Analysis)作为一种定量的方法,将从数据分析的角度,给出一个更准确更细致的分类工具。
聚类分析又称群分析,是对多个样本或者指标进行定量分类的一种多元统计分析方法。对样本进行分类称为Q型聚类分析,对指标进行分类称为R型聚类分析。
Q型聚类分析
-
样本的相似性度量
要用数量化的方法对事物进行分类,就必需要用数量化的方法描述事物之间的相似度。一个事物常常需要多个变量来刻画, 如果对于一群有待分类的样本点需要用 p p p 个变量描述,则每个样本点可以看成是 R p R^p Rp 空间中的一个点。因此,很自然想到可以用距离来度量样本带你之间的相似程度。
记 Ω \Omega Ω 为样本点击,距离 d ( ⋅ , ⋅ ) d(\cdot,\cdot) d(⋅,⋅) 是 Ω × Ω → R + \Omega \times \Omega \to R^+ Ω×Ω→R+ 的一个函数,满足条件
- d ( x , y ) ≥ 0 , x , y ∈ Ω d(x,y) \geq 0,\quad x,y\in \Omega d(x,y)≥0,x,y∈Ω
- d ( x , y ) = 0 d(x,y)=0 d(x,y)=0 ,当且仅当 x = y x=y x=y 。
- d ( x , y ) = d ( y , x ) , x , y ∈ Ω d(x,y)=d(y,x),\quad x,y \in \Omega d(x,y)=d(y,x),x,y∈Ω
- d ( x , y ) ≤ d ( x , z ) + d ( z , y ) , x , y , z ∈ Ω d(x,y)\leq d(x,z)+d(z,y),\quad x,y,z\in \Omega d(x,y)≤d(x,z)+d(z,y),x,y,z∈Ω
这一距离的定义是我们所熟知的,它满足正定性、对称性和三角不等式。在聚类分析中,对定量变量,最常用的是闵氏(Minkowski)距离,即
d q ( x , y ) = [ ∑ k = 1 p ∣ x k − y k ∣ q ] 1 q , q > 0 d_q(x,y)=[\sum _{k=1} ^p |x_k-y_k|^q]^{\frac{1}{q}},\quad q>0 dq(x,y)=[k=1∑p∣xk−yk∣q]q1,q>0
当 q = 1 , 2 q=1,2 q=1,2 或 q → + ∞ q\to +\infin q→+∞ 时,则分别得到:-
绝对距离
d 1 ( x , y ) = ∑ k = 1 p ∣ x k − y k ∣ (1) d_1(x,y)=\sum_{k=1}^{p}|x_k-y_k| \tag{1} d1(x,y)=k=1∑p∣xk−yk∣(1) -
欧几里得距离
d 2 ( x , y ) = [ ∑ k = 1 p ∣ x k − y k ∣ 2 ] 1 2 (2) d_2(x,y)=[\sum_{k=1}^{p}|x_k-y_k|^2]^\frac{1}{2} \tag{2} d2(x,y)=[k=1∑p∣xk−yk∣2]21(2) -
切比雪夫距离
d ∞ ( x , y ) = max 1 ≤ k ≤ p ∣ x k − y k ∣ (3) d_\infin(x,y)=\max _{1\leq k\leq p}|x_k-y_k| \tag{3} d∞(x,y)=1≤k≤pmax∣xk−yk∣(3) -
马氏距离
d ( x , y ) = ( x − y ) T ∑ − 1 ( x − y ) (4) d(x,y)=\sqrt{(x-y)^T\mathbf{\sum}^{-1}(x-y)} \tag{4} d(x,y)=(x−y)T∑−1(x−y)(4)
式中: x , y x,y x,y 为来自 p p p 维总体 Z Z Z 的样本观测值; ∑ \sum ∑ 为 Z Z Z 的协方差矩阵,实际中 ∑ \sum ∑ 往往是未知的,常常需要用样本协方差来估计。马氏距离对一切线性变换是不变的,故不受量纲的影响。
在Minkowski距离中,最常用的是欧几里得距离,它的主要有点是当坐标轴进行正交旋转的时候,欧氏距离是保持不变的。因此,如果对原坐标系进行平移或者旋转变换,则变换后样本点检的距离和变换前完全相同。
值得注意的是,在采用Minkowski距离时,一定要采用相同量纲的变量。当变量的量纲不同时,观测值得变易范围相差悬殊,建议首先进行数据得标准化处理,然后再计算距离。再采用Minkowski距离时,还应尽可能避免变量的多重相关性。多重相关性所造成的信息重叠,会片面强调某些变量的重要性。
-
类与类之家你的相似性度量
如果有两个样本类 G 1 G_1 G1 和 G 2 G_2 G2,可以用以下方法度量他们之间的距离。
-
最短距离法(Nearest Neighbor or Single Linkage Method)
D ( G 1 , G 2 ) = min x i ∈ G 1 y j ∈ G 2 { d ( x i , y j ) } (5) D(G_1,G_2)=\min _{x_i \in G_1 \\y_j \in G_2} \{d(x_i,y_j)\} \tag{5} D(G1,G2)=xi∈G1yj∈G2min{d(xi,yj)}(5)
它的直观意义为两个类中最近两点间的距离。 -
最长距离法(Farthest Neighbo or Complete Linkage Method)
D ( G 1 , G 2 ) = max x i ∈ G 1 y j ∈ G 2 { d ( x i , y j ) } (6) D(G_1,G_2)=\max _{x_i \in G_1 \\y_j \in G_2} \{d(x_i,y_j)\} \tag{6} D(G1,G2)=xi∈G1yj∈G2max{d(xi,yj)}(6)
它的直观意义为两个类中最远两点间的距离。 -
重心法(Centroid Method)
D ( G 1 , G 2 ) = d ( x ˉ , y ˉ ) (7) D(G_1,G_2)=d(\bar{x},\bar{y}) \tag{7} D(G1,G2)=d(xˉ,yˉ)(7)
式中: x ˉ , y ˉ \bar{x},\bar{y} xˉ,yˉ 分别为 G 1 , G 2 G_1,G_2 G1,G2 的重心。 -
类平均法(Group Average Method)
D ( G 1 , G 2 ) = 1 n 1 n 2 ∑ x i ∈ G 1 ∑ x j ∈ G 2 d ( x i , x j ) (8) D(G_1,G_2)=\frac{1}{n_1n_2}\sum_{x_i\in G_1}\sum_{x_j\in G_2}d(x_i,x_j) \tag{8} D(G1,G2)=n1n21xi∈G1∑xj∈G2∑d(xi,xj)(8)
它等于 G 1 , G 2 G_1,G_2 G1,G2 两个样本点距离的平均, n 1 , n 2 n_1,n_2 n1,n2 分别为 G 1 , G 2 G_1,G_2 G1,G2 中样本点的个数 -
离差平方和法(Sum of Squares Method)
若记
D 1 ( G 1 , G 2 ) = ∑ x i ∈ G 1 ( x i − x ˉ 1 ) T ( x i − x ˉ 1 ) D 2 ( G 1 , G 2 ) = ∑ x j ∈ G 2 ( x j − x ˉ 2 ) T ( x j − x ˉ 2 ) D 12 = ∑ x k ∈ G 1 ∪ G 2 ( x k − x ˉ ) T ( x k − x ˉ ) D_1(G_1,G_2)=\sum_{x_i\in G_1}(x_i-\bar{x}_1)^T(x_i-\bar{x}_1)\\ D_2(G_1,G_2)=\sum_{x_j\in G_2}(x_j-\bar{x}_2)^T(x_j-\bar{x}_2)\\ D_{12}=\sum _{x_k \in G_1 \cup G_2} (x_k-\bar{x})^T(x_k-\bar{x}) D1(G1,G2)=xi∈G1∑(xi−xˉ1)T(xi−xˉ1)D2(G1,G2)=xj∈G2∑(xj−xˉ2)T(xj−xˉ2)D12=xk∈G1∪G2∑(xk−xˉ)T(xk−xˉ)
式中
x ˉ 1 = 1 n 1 ∑ x i ∈ G 1 x i , x ˉ 2 = 1 n 2 ∑ x j ∈ G 2 x j , x ˉ = 1 n 1 + n 2 ∑ x k ∈ G 1 ∪ G 2 x k \bar{x}_1=\frac{1}{n_1}\sum_{x_i \in G_1}x_i,\quad \bar{x}_2=\frac{1}{n_2}\sum _{x_j\in G_2}x_j,\quad \bar{x}=\frac{1}{n_1+n_2}\sum _{x_k\in G_1\cup G_2}x_k xˉ1=n11xi∈G1∑xi,xˉ2=n21xj∈G2∑xj,xˉ=n1+n21xk∈G1∪G2∑xk
则定义
D ( G 1 , G 2 ) = D 12 − D 1 − D 2 (9) D(G_1,G_2)=D_{12}-D_1-D_2 \tag{9} D(G1,G2)=D12−D1−D2(9)
事实上,若 G 1 , G 2 G_1,G_2 G1,G2 内部点与点之间距离很小,则它们能很好地各自聚为一类,并且这两类又能充分分离,这时必然有 D = D 12 − D 1 − D 2 D=D_{12}-D_1-D_2 D=D12−D1−D2 很大。因此,按照定义可以认为,两类 G 1 , G 2 G_1,G_2 G1,G2 之间的距离充分大。离差平方和法又称为 Ward 法。
-
-
聚类图
Q型聚类结果可以由一个聚类图展示出来
例如平面上七个点 w 1 , ⋯ , w 7 w_1,\cdots,w_7 w1,⋯,w7 ,可以用聚类图来表示聚类结果。

记 Ω = { w 1 , ⋯ , w 7 } \Omega=\{w_1,\cdots,w_7\} Ω={w1,⋯,w7} ,聚类结果如下:当距离值为 f 5 f_5 f5 时,分为一类,即
G 1 = { w 1 , w 2 , w 3 , w 4 , w 5 , w 6 , w 7 } G_1=\{w_1,w_2,w_3,w_4,w_5,w_6,w_7\} G1={w1,w2,w3,w4,w5,w6,w7}
当距离值为 f 4 f_4 f4 时,分为两类,即
G 1 = { w 1 , w 2 , w 3 } , G 2 = { w 4 , w 5 , w 6 , w 7 } G_1=\{w_1,w_2,w_3\},\ G_2=\{w_4,w_5,w_6,w_7\} G1={w1,w2,w3}, G2={w4,w5,w6,w7}
当距离值为 f 3 f_3 f3 时,分为三类,即
G 1 = { w 1 , w 2 , w 3 } , G 2 = { w 4 , w 5 , w 6 } , G 3 = { w 7 } G_1=\{w_1,w_2,w_3\},\ G_2=\{w_4,w_5,w_6\},\ G_3=\{w_7\} G1={w1,w2,w3}, G2={w4,w5,w6}, G3={w7}
当距离值为 f 2 f_2 f2 时,分为四类,即
G 1 = { w 1 , w 2 , w 3 } , G 2 = { w 4 , w 5 } , G 3 = { w 6 } , G 4 = { w 7 } G_1=\{w_1,w_2,w_3\},\ G_2=\{w_4,w_5\},\ G_3=\{w_6\},\ G_4=\{w_7\} G1={w1,w2,w3}, G2={w4,w5}, G3={w6}, G4={w7}
当距离值为
f
1
f_1
f1 时,分为六类,即
G
1
=
{
w
4
,
w
5
}
,
G
2
=
{
w
1
}
,
G
3
=
{
w
2
}
,
G
4
=
{
w
3
}
,
G
5
=
{
w
6
}
,
G
6
=
{
w
7
}
G_1=\{w_4,w_5\},\ G_2=\{w_1\},\ G_3=\{w_2\},\ G_4=\{w_3\},\ G_5=\{w_6\},\ G_6=\{w_7\}
G1={w4,w5}, G2={w1}, G3={w2}, G4={w3}, G5={w6}, G6={w7}
当距离小于
f
1
f_1
f1 时,分为七类,每个点自成一类。
怎么才能生成聚类图?
设 Ω = { w 1 , w 2 , w 3 , w 4 , w 5 , w 6 , w 7 } \Omega=\{w_1,w_2,w_3,w_4,w_5,w_6,w_7\} Ω={w1,w2,w3,w4,w5,w6,w7},具体步骤如下:
(1)计算 n n n 个样本点两两之间的距离 { d i j } \{d_{ij}\} {dij},记为矩阵 D = ( d i j ) n × n \mathbf{D}=(d_{ij})_{n\times n} D=(dij)n×n
(2)首先构造 n n n 个类,每一个类中只包含一个样本点,每一类的平台高度为0
(3)合并距离最近的两类为新类,并以这两类之间的距离值作为聚类图中的平台高度。
(4)计算新类与当前各类的距离,若类的个数已经为1,转入步骤(5),否则重复步骤(3)
(5)画出聚类图
(6)决定类的个数和如何分类
-
最短距离法的聚类举例
如果使用最短距离法来测量类与类之家你的距离,即称其为系统聚类法中的最短距离法,也成为最邻近法。
例:设有5个销售员 w 1 , w 2 , w 3 , w 4 , w 5 w_1,w_2,w_3,w_4,w_5 w1,w2,w3,w4,w5,他们的销售业绩有二维变量 ( v 1 , v 2 ) (v_1,v_2) (v1,v2) 描述
销售员 v 1 v_1 v1 (销售量)/百件 v 2 v_2 v2 (回收款项)/万元 w 1 w_1 w1 1 0 w 2 w_2 w2 1 1 w 3 w_3 w3 3 2 w 4 w_4 w4 4 3 w 5 w_5 w5 2 5 记销售员 w i w_i wi 的销售业绩为 ( v i 1 , v i 2 ) (v_{i1},v_{i2}) (vi1,vi2)。使用绝对值距离来测量点与点之间的距离,使用最短距离法来测量类与类之间的距离,即
d ( w i , w j ) = ∑ k = 1 2 ∣ v i k − v j k ∣ , D ( G p , G q ) = min w i ∈ G p w j ∈ G q { d ( w i , w j ) } d(w_i,w_j)=\sum _{k=1} ^2 |v_{ik}-v_{jk}|,\quad D(G_p,G_q)=\min _{w_i\in G_p \ w_j\in G_q}\{d(w_i,w_j)\} d(wi,wj)=k=1∑2∣vik−vjk∣,D(Gp,Gq)=wi∈Gp wj∈Gqmin{d(wi,wj)}
由距离公式 d ( ⋅ , ⋅ ) d(\cdot,\cdot) d(⋅,⋅) 可以计算出距离矩阵
[ 0 1 4 6 6 0 3 5 5 0 2 4 0 4 0 ] \left[\begin{matrix} 0&1&4&6&6\\ &0&3&5&5\\ & &0&2&4\\ & & &0&4\\ & & & &0 \end{matrix}\right] ⎣⎢⎢⎢⎢⎡010430652065440⎦⎥⎥⎥⎥⎤
第一步: 所有元素自成一类 H 1 = { w 1 , w 2 , w 3 , w 4 , w 5 } H_1=\{w_1,w_2,w_3,w_4,w_5\} H1={w1,w2,w3,w4,w5}。每一类的平台高度均为0,即 f ( w i ) = 0 f(w_i)=0 f(wi)=0。显然此时 D ( G p , G q ) = d ( w p , w q ) D(G_p,G_q)=d(w_p,w_q) D(Gp,Gq)=d(wp,wq)。第二步: 取新类的平台高度为1,把 w 1 , w 2 w_1,w_2 w1,w2 合并为一个新类 h 6 h_6 h6 ,此时的分类情况为
H 2 = { h 6 , w 3 , w 4 , w 5 } H_2=\{h_6,w_3,w_4,w_5\} H2={h6,w3,w4,w5}
第三步: 取新类的平台高度为2,把 w 3 , w 4 w_3,w_4 w3,w4 合并为一个新类 h 7 h_7 h7 ,此时的分类情况为
H 3 = { h 6 , h 7 , w 5 } H_3=\{h_6,h_7,w_5\} H3={h6,h7,w5}
第四步: 取新类的平台高度为3,由于 h 6 , h 7 h_6,h_7 h6,h7 之间按照最短距离法计算的距离为3,所以将 h 6 , h 7 h_6,h_7 h6,h7 合并为一个新类 h 8 h_8 h8 ,此时的分类情况为
H 4 = { h 8 , w 5 } H_4=\{h_8,w_5\} H4={h8,w5}
第五步: 取新类的平台高度为4,把 h 8 , w 5 h_8,w_5 h8,w5 合并成一个新类 h 9 h_9 h9 ,此时的分类情况为
H 5 = { h 9 } H_5=\{h_9\} H5={h9}
做出聚类图及二叉树图
使用Matlab实现其功能
a=[1,0;1,1;3,2;4,3;2,5]; [m,n]=size(a); d=zeros(m); d=mandist(a'); d=tril(d); nd=nonzeros(d); nd=union([],nd); for i=1:m-1 nd_min=min(nd); [row,col]=find(d==nd_min); tm=union(row,col); tm=reshape(tm,1,length(tm)); fprintf('第%d次合成,平台高度为%d时的分类结果为:%s\n',i,nd_min,int2str(tm)); nd(nd==nd_min)=[]; if length(nd)==0 break; end end还可以利用Matlab的统计工具箱
a=[1,0;1,1;3,2;4,3;2,5]; y=pdist(a,'cityblock'); %计算绝对值距离 z=linkage(y); %生成等级聚类树 dendrogram(z); %画聚类图 T=cluster(z,'maxclust',3); %把对象划分成三类 for i=1:3 tm=find(T==i); tm=reshape(tm,1,length(tm)); fprintf('第%d类的有%s\n',i,int2str(tm)); end
-
Matlab中聚类分析的相关命令
-
pdistY=pdist(X)计算 m × n m\times n m×n 矩阵 X \mathbf{X} X 中两两对象间的欧氏距离。对于有 m m m 个对象组成的数据集,共有 ( m − 1 ) ⋅ m 2 \frac{(m-1)\cdot m}{2} 2(m−1)⋅m 个两两对象组合。输出
Y是包含距离信息的长度为 ( m − 1 ) ⋅ m 2 \frac{(m-1)\cdot m}{2} 2(m−1)⋅m 的向量。可以用squareform将其转换成方阵,这样可以使得矩阵中的元素 ( i , j ) (i,j) (i,j) 对应原始数据集中对象 i i i 和 j j j 之间的距离。Y=pdist(X,'metric)中用metric指定的方法计算矩阵 X \mathbf{X} X 中对象间的距离。参数 含义 参数 含义 euclidean欧氏距离(默认) hamming汉明距离 seuclidean标准欧几里得距离 custom distance fuction自定义函数距离 cityblock绝对值距离 cosine1-两个向量夹角余弦 minkowski闵氏距离 correlation1-样本相关系数 chebychev切比雪夫距离 spearman1-样本Spearman秩相关系数 mahalanobis马氏距离 jaccard1-Jaccard系数 -
linkageZ=linkage(Y)使用最短距离法生成具有层次结构的聚类树。输入矩阵Y为pdist函数输出的 m ( m − 1 ) 2 \frac{m(m-1)}{2} 2m(m−1) 维距离行向量Z=linkage(Y,'method')使用由method指定的算法计算生成聚类树。参数 含义 参数 含义 single最短距离(默认) median赋权重心距离 average无权平均距离 ward离差平方和方法 centroid重心距离 weighted赋权平均距离 complete最大距离 输出的
Z为包含聚类树信息的 ( m − 1 ) × 3 (m-1)\times 3 (m−1)×3 的矩阵。聚类树上的叶节点为原始数据集中的对象,由 1 ∼ m 1\sim m 1∼m。它们是单元素的类,级别更高的类都是由它们生成的。对于Z中第 j j j 行每个新生成的类,其索引为 m + j m+j m+j,其中 m m m 为初始叶节点的数量。第1列和第2列,即 Z ( : , [ 1 : 2 ] ) Z(:,[1:2]) Z(:,[1:2]) 包含了被两两连接生成一个新类的所有对象的索引。生成的新类索引为 m + j m+j m+j 。共有 m − 1 m-1 m−1 个级别更高的类,它们对应于聚类树中的内部节点。第3列 Z ( : , 3 ) Z(:,3) Z(:,3) 包含了相应的在类中的两两对象之间的连接距离。 -
clusterT=cluster(Z,'cutoff',c)从连接输出中创建聚类。cutoff为定义cluster函数如何生成聚类的阈值。当 0 < c u t o f f < 2 0<cutoff<2 0<cutoff<2 时,cutoff作为不一致系数的阈值,不一致系数对聚类树中对象间的差异进行量化,如果连接的不一致系数大语阈值,则cluster函数将其作为聚类分组的边界。当 c u t o f f ≥ 2 cutoff\geq2 cutoff≥2 ,cutoff作为包含在聚类树中的最大分类数。T=cluster(Z,'cutoff',c,'depth',d)从连接输出中创建聚类。参数depth制定了聚类树中的层数,进行不一致系数计算的时候要用到。不一致系数将聚类树中两对象连接于相邻的连接进行比较。输出
T为大小为 m m m 的向量,它用数字对每个对象所属的类进行表示。为了找到包含在类 i i i 中的来自原始数据集的对象,可以用find(T==i) -
zsore(X)
对数据矩阵进行标准化处理,处理方法为
x ˉ i j = x i j − x ˉ j s j \bar{x}_{ij}=\frac{x_{ij}-\bar{x}_j}{s_j} xˉij=sjxij−xˉj
式中: x ˉ j , s j \bar{x}_j,s_j xˉj,sj 为矩阵 X = ( x i j ) m × n \mathbf{X}=(x_{ij})_{m\times n} X=(xij)m×n 每一列的均值和标准差。-
H=dendrogram(Z,P)由
linkage产生的数据矩阵Z画聚类树状图。P为节点数,默认值是30. -
T=clusterdata(X,cutoff)将矩阵 X \mathbf{X} X 的数据分类。 X \mathbf{X} X 为 m × n m\times n m×n 矩阵,被看成 m m m 个 n n n 维行向量。它与以下几个命令的效果等价。
Y=pdist(X); Z=linkage(Y,'single'); T=cluster(Z,cutoff);
-
R型聚类法
在实际工作中,变量聚类法的应用也是十分重要的。在系统分析嚯评估过程中,为了避免遗漏某些重要的因素,往往在一开始选取指标的时候,尽可能多地考虑所有的相关因素。而这样做的结果,则是变量过多,变量间的相关度高,给系统分析和建模带来了很大不便。因此,人们常常希望能够研究变量间的相似关系,按照变量的相似关系聚合成若干类,进而找出影响系统的主要因素。
-
变量相似性度量
在对变量进行聚类分析的时候,首先要确定变量的相似性度量,常用的变量相似性度量由两种
-
相关系数。
记变量 x j x_j xj 的取值 ( x 1 j , x 2 j , ⋯ , x n j ) T ∈ R n , ( j = 1 , 2 , ⋯ , m ) (x_{1j},x_{2j},\cdots,x_{nj})^T\in \mathbf{R}^n,\ (j=1,2,\cdots,m) (x1j,x2j,⋯,xnj)T∈Rn, (j=1,2,⋯,m) 。则可以用两个变量 x j x_j xj 和 x k x_k xk 的样本相关系数作为它们的相似性度量,即
r j k = ∑ i = 1 n ( x i j − x ˉ j ) ( x i k − x ˉ k ) [ ∑ i = 1 n ( x i j − x ˉ j ) 2 ∑ i = 1 n ( x i k − x ˉ k ) 2 ] 1 2 (10) r_{jk}=\frac{\sum \limits_{i=1} ^n (x_{ij}-\bar{x}_j)(x_{ik}-\bar{x}_k)}{[\sum \limits_{i=1} ^n(x_{ij}-\bar{x}_j)^2\sum \limits _{i=1} ^n (x_{ik}-\bar{x}_k)^2]^\frac{1}{2}} \tag{10} rjk=[i=1∑n(xij−xˉj)2i=1∑n(xik−xˉk)2]21i=1∑n(xij−xˉj)(xik−xˉk)(10)
在对变量进行聚类分析时,利用相关系数矩阵式最多的。 -
夹角余弦
可以直接用两变量 x j x_j xj 和 x k x_k xk 的夹角余弦 r j k r_{jk} rjk 来定义它们的相似性度量
r j k = ∑ i = 1 n x i j x i k ( ∑ i = 1 n x i j 2 ∑ i = 1 n x i k 2 ) 1 2 (11) r_{jk}=\frac{\sum \limits _{i=1} ^n x_{ij}x_{ik}}{(\sum\limits_{i=1}^nx_{ij}^2\sum\limits_{i=1}^nx_{ik}^2)^\frac{1}{2}} \tag{11} rjk=(i=1∑nxij2i=1∑nxik2)21i=1∑nxijxik(11)
各种定义的相似度量均应该具有以下两个性质
① ∣ r j k ∣ ≤ 1 |r_{jk}|\leq 1 ∣rjk∣≤1 对于一切的 j , k j,k j,k 。
② r j k = r k j r_{jk}=r_{kj} rjk=rkj,对于一切的 j , k j,k j,k。
∣ r j k ∣ |r_{jk}| ∣rjk∣ 越接近1, x j x_j xj 和 x k x_k xk 越相关或约相似。 ∣ r j k ∣ |r_{jk}| ∣rjk∣ 越接近0, x j x_j xj 和 x k x_k xk 的相似性越弱。
-
-
变量聚类法
类似于样本集合聚类分析中最常用的最短距离法,最长距离法等,变量聚类法采用与系统聚类法相同的思路和过程。在变量聚类问题中,常用的由最长距离法和最短距离法等。
-
最长距离法
在最长距离法中,定义两类变量的距离为
R ( G 1 , G 2 ) = max x j ∈ G 1 x k ∈ G 2 { d j k } (12) R(G_1,G_2)=\max_{x_j\in G_1\\x_k\in G_2}\{d_{jk}\} \tag{12} R(G1,G2)=xj∈G1xk∈G2max{djk}(12)
式中: d j k = 1 − ∣ r j k ∣ d_{jk}=1-|r_{jk}| djk=1−∣rjk∣ 或者 d j k 2 = 1 − r j k 2 d_{jk}^2=1-r_{jk}^2 djk2=1−rjk2,此时 R ( G 1 , G 2 ) R(G_1,G_2) R(G1,G2) 与两类中相似性最小的两变量之间的相似性度量有关。 -
最短距离法
在最短距离法中,定义两类变量的距离为
R ( G 1 , G 2 ) = min x j ∈ G 1 x k ∈ G 2 { d j k } (13) R(G_1,G_2)=\min_{x_j\in G_1\\x_k\in G_2}\{d_{jk}\} \tag{13} R(G1,G2)=xj∈G1xk∈G2min{djk}(13)
式中: d j k = 1 − ∣ r j k ∣ d_{jk}=1-|r_{jk}| djk=1−∣rjk∣ 或者 d j k 2 = 1 − r j k 2 d_{jk}^2=1-r_{jk}^2 djk2=1−rjk2,此时 R ( G 1 , G 2 ) R(G_1,G_2) R(G1,G2) 与两类中相似性最大的两变量之间的相似性度量有关。
例:服装标准制定中的变量聚类法。在服装标准制定中,对成年女子各部位尺寸进行统计,通过14个部位的测量资料,获得各因素之间的相关系数表。

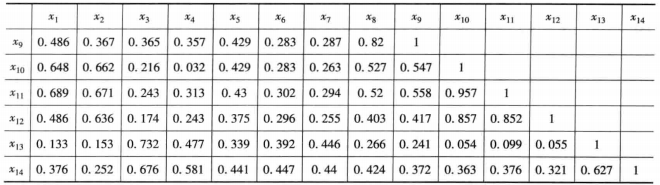
其中: x 1 x_1 x1 为上身长, x 2 x_2 x2 为手臂长, x 3 x_3 x3 为胸围, x 4 x_4 x4 为颈围, x 5 x_5 x5 为总肩围, x 6 x_6 x6 为总胸宽, x 7 x_7 x7 为后背宽, x 8 x_8 x8 为前腰节高, x 9 x_9 x9 为后腰节高, x 10 x_{10} x10 为全身长, x 11 x_{11} x11 为身高, x 12 x_{12} x12 为下身长, x 13 x_{13} x13 为腰围, x 14 x_{14} x14 为臀围。用最大系数法对这14个变量进行系统聚类。具体代码及结果如下
a=textread('ch.txt'); d=1-abs(a); %进行数据变换,把相关系数转化为距离 d=tril(d); b=nonzeros(d); b=b'; z=linkage(b,'complete'); %按照最长距离法聚类 y=cluster(z,'maxclust',2); %把变量分为两类 h=dendrogram(z); %画出聚类图
-






















 4560
4560











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








