【Stanford机器学习笔记】4-Regularization for Solving the Problem of Overfitting

前面讲了机器学习的两种应用：回归和分类。两种主要模型：线性回归模型和逻辑回归模型。为了使训练出来的机器学习模型具有普遍的泛化能力，需要对模型进行优化，例如欠拟合和过拟合问题，正则化算法正是用于解决机器学习算法中的拟合问题。

1. The problem of Underfitting and Overfitting

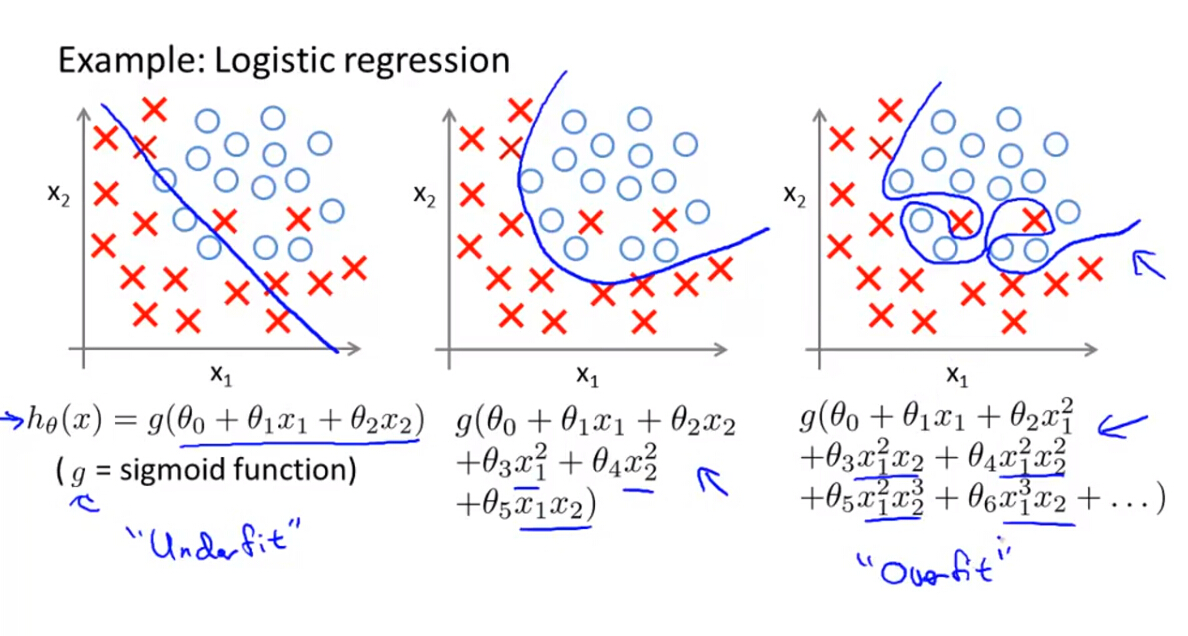
（1）线性回归和逻辑回归均存在过度拟合和欠拟合的问题

• 过度拟合的问题是，如果我们有很多特征变量，则训练出来的假设函数模型会对训练样本拟合的很好，但是对于新加入的数据，假设函数模型不能拟合的很好，又称为High Variance。
• 欠拟合则是假设函数不能对训练样本进行很好的拟合，又称为High Bias。

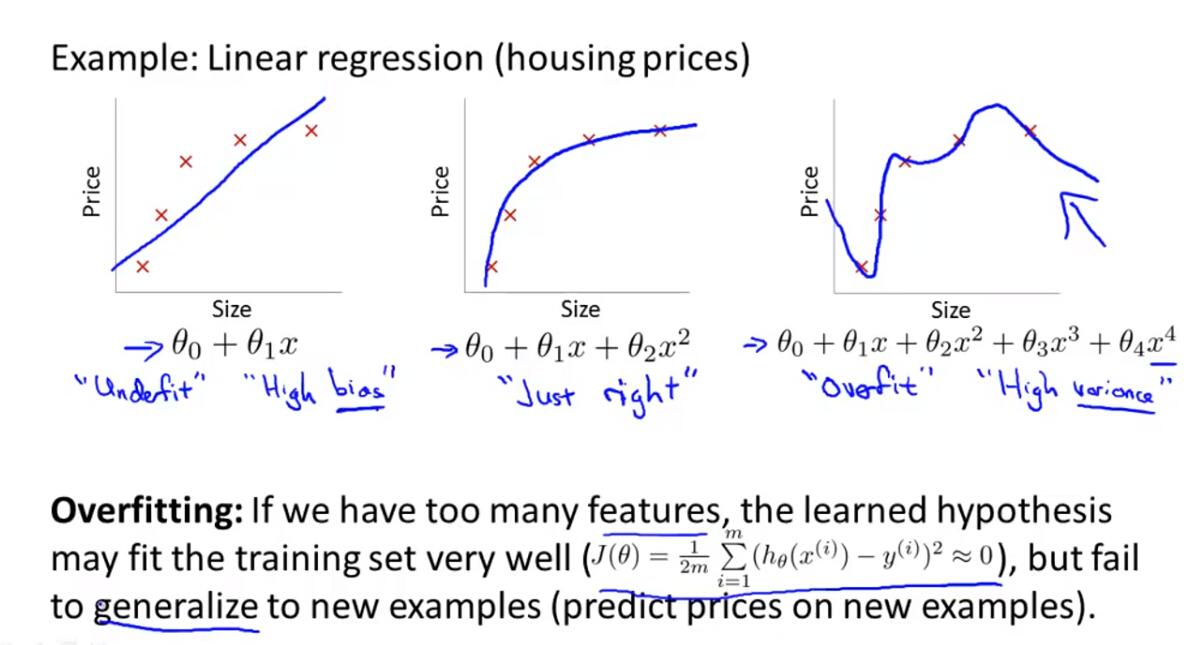
（2）如果训练样本较少，特征变量较多，则就可能出现过度拟合的问题，解决过度拟合的方法有两种：

• 减少特征变量的数量，但是这样也减小了数据的信息
  
  • 手动减小特征变量数量
  • 利用算法自动减小特征变量数量
• 正则化算法
  
  • 正则化算法主要是保留所有特征变量，但是对所有参数加上权重限制每个参数的贡献度

2. Cost Function with regularization term

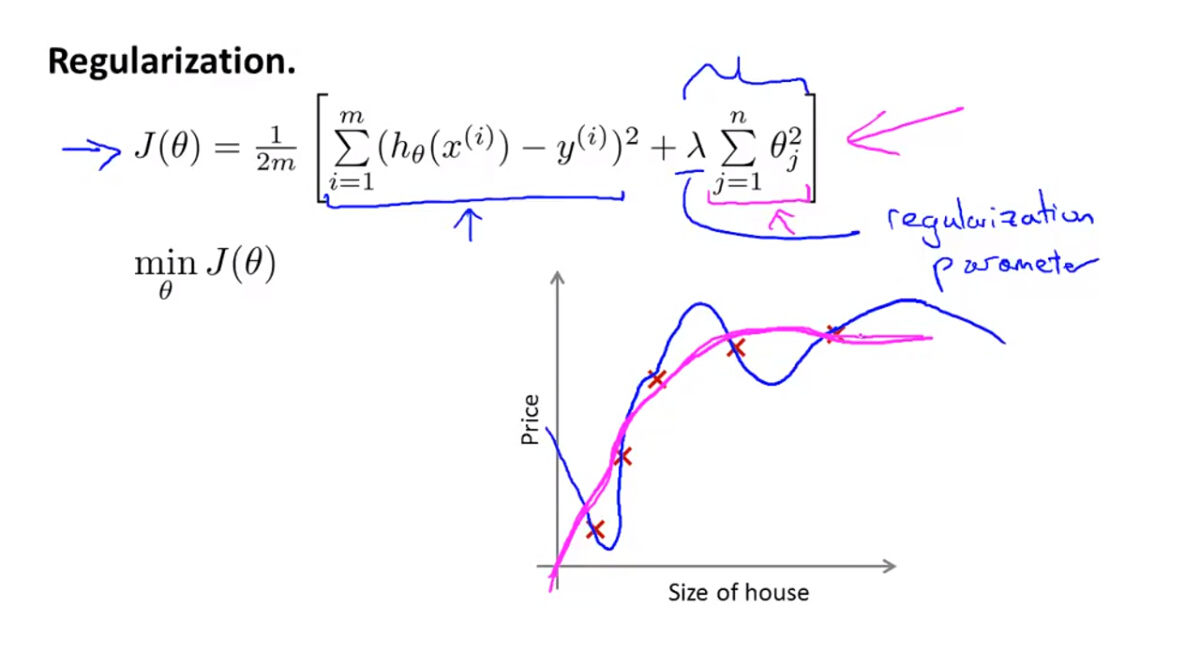
（1）加入正则化项的代价函数变为：

$$J(\theta)=\frac{1}{2m} [\sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})^2+\lambda \sum_{j=1}^n \theta_j^2]$$

（2）正则化参数$\lambda$的使用

• 如果$\lambda$过大，则对于参数的惩罚就会增大，使得参数接近0，使得假设函数模型变得过于简单，就会出现欠拟合问题。
• 如果$\lambda$过小，则对于参数的惩罚就会影响不大，原模型复杂，使得假设函数模型变得过于复杂，就会出现过拟合问题。

（3）如何选择正则化参数$\lambda$

在接下来的课程中将会介绍一些算法用于正则化参数$\lambda$的自动选择。

3. Regularized Linear Regression

加入了正则化项后，线性回归模型的代价函数$J(\theta)$发生了改变，

$$J(\theta)=\frac{1}{2m} [\sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})^2+\lambda \sum_{j=1}^n \theta_j^2]$$ 所以在进行训练时，也发生了改变，前面讲了，线性回归模型有两种优化方法：一是梯度下降法；二是正规方程法，下面分别介绍。

（1）梯度下降法
$J(\theta)$改变以后，主要改变了梯度下降算法中的导数项求解过程，优化的基本过程是：

$$\theta_0:=\theta_0-\alpha \frac{1}{m}\sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})x_0^{(i)}\\ \theta_j:=\theta_j(1-\alpha \frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}$$

Notes: 正则化不对第一个参数项$\theta_0$进行正则化，只对后面的参数进行正则化。

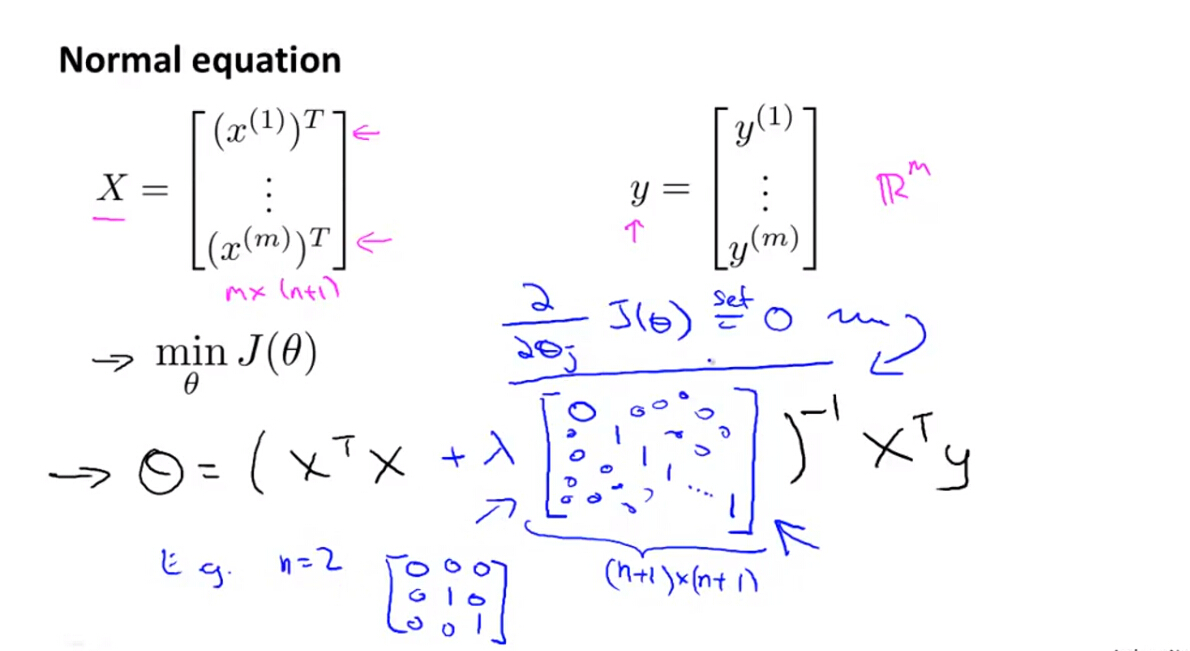
（2）正规方程法
$J(\theta)$改变以后，主要改变了参数解的形式，具体如下：

$$\theta=(X^TX+\lambda \left[ \begin{matrix} 0&0&0&0\\ 0&1&0&0\\ 0&0&\ddots&0\\ 0&0&0&1 \end{matrix} \right]_{(n+1)*(n+1)})X^Ty$$

（3）不可逆的情况
当不使用正则化项时，利用正规方程解算线性回归模型时，且当$m\le n$时，就会出现$X^TX$不可逆的问题，所以此时不能利用正规方程进行求解。但是当加入了正则化项时，就不存在这个问题。

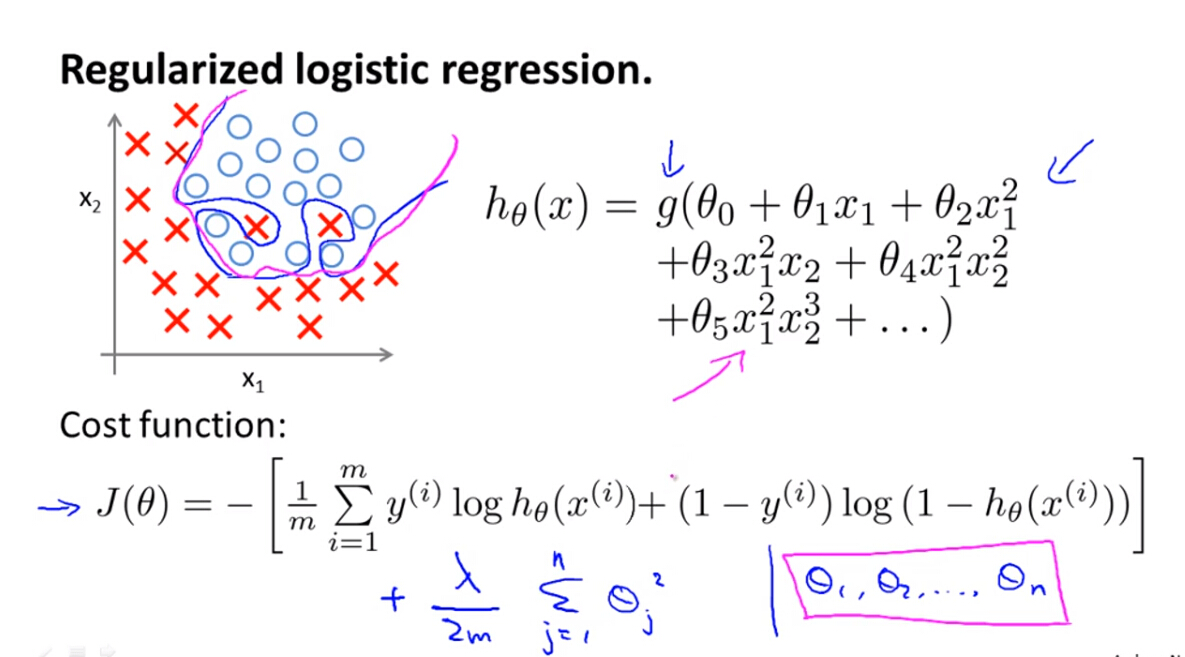
3. Regularized Logistic Regression

（1）加入正则化项后，逻辑回归模型的代价函数变为：

$$J(\theta)=-[\frac{1}{m} \sum_{i=1}^m y^{(i)} log(h_{\theta}(x^{(i)}))+(1-y^{(i)}) log(1-h_{\theta}(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2$$
前面讲了两种逻辑回归模型算法：一是梯度下降法；二是高级优化算法，下面分别介绍。

（2）梯度下降法
$J(\theta)$改变以后，主要改变了梯度下降算法中的导数项求解过程，优化的基本过程是：

$$\theta_0:=\theta_0-\alpha \frac{1}{m}\sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})x_0^{(i)}\\ \theta_j:=\theta_j-\alpha[\frac{1}{m}\sum_{i=1}^m (h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda}{m}\theta_j]$$

Notes: 正则化不对第一个参数项$\theta_0$进行正则化，只对后面的参数进行正则化。

（3）高级优化算法
利用高级优化算法求解逻辑回归模型，主要是将正则化项加入到解算代价函数和求导函数的代码中，然后利用高级优化算法解算最优参数。