R-建模(广义)线性(加性、混合)模型

1、R 中的简单线性模型

$$Y_i={\beta }_0+{\beta }_1{X}_i+{ϵ}_i,{ϵ}_i\sim N(0,{\sigma }^2)$$

mod <- lm(formula = mpg ~ wt,data = mtcars)
#mod <- lm(formula = mpg ~ wt + 0,data = mtcars) ### 生成不带截距项的简单线性模型
summary(mod)

Multiple R-squared:在一元线性回归中，Pearson相关系数R的平方等于线性回归的R²(Multiple R-squared)。这是因为在一元线性回归中，只有一个自变量和一个因变量，因此两个变量之间的线性相关程度和自变量对因变量的解释程度是一致的。但在多元线性回归中，Pearson相关系数R和线性回归的R²可能不相等，因为多元线性回归中有多个自变量，而Pearson相关系数R只能衡量两个变量之间的线性相关程度。

提取${\beta }_1$ 的97.5% 置信区间 ：

mod$coefficients[[2]] - qnorm(0.975) * summary(mod)$coefficients[2,2]
mod$coefficients[[2]] + qnorm(0.975) * summary(mod)$coefficients[2,2]

预测新的数据： predict(mod,newdata = data.frame(wt = c(1,2,3))) ### 返回一个 vector 数据类型

2、R 中的多元线性模型

2.1 多元线性模型

$$Y_i={\beta }_0+{\beta }_1{X}_i+{\beta }_2{X}_j+...+{ϵ}_i,{ϵ}_i\sim N(0,{\sigma }^2)$$

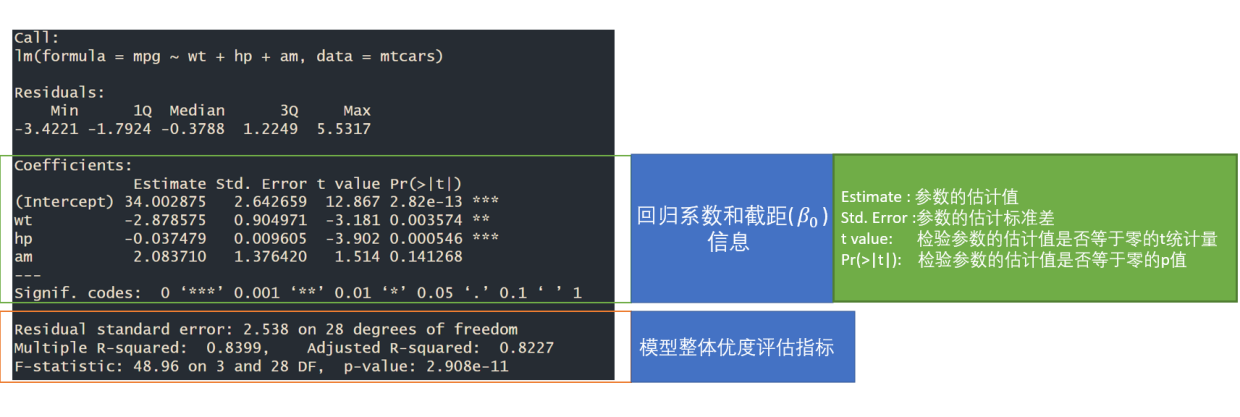
mod <- lm(formula = mpg ~ wt + hp + am,data = mtcars)  #formula = y~.  表示纳入数据框的所有变量进行多元线性回归
summary(mod)

Multiple R-squared: 随着变量的增加，模型的拟合优度始终提升；
Adjusted R-squared: 根据变量数目进行调整R²，在多变量的前提下能更准确地反映模型的拟合优度，同时暗示变量不是越多越好。

由于R²无法回答模型是否统计显著的问题，进而提出了基于模型F统计量检验: F = M S E M S M F = \frac {MSE}{MSM}