堆排序实现优先队列（Priority queue）

1.大体思路
队列内使用最大堆排序，将最大值放在根节点，出队操即每次取出堆顶值，并将队列长度减1；入队操作则是在队列末尾加入待入队的数字，并使用之前函数BuildMaxHeap(Arr, Len)重新建立最大堆；获得队首值则直接返回Arr[0]即可，每次操作前检查队列是否为空。
2.代码如下

#include <iostream>
#include <ctime>
#include <windows.h>
using namespace std;
int Len;
int Arr[100];

//struct HeapStruct {
//    int Capacity;
//    int Size;
//    int *Element;
//};

//HeapStruct* Initialize(int MaxNum) {

//}

void Swape(int *p, int *q) {
    int tmp = *p;
    *p = *q;
    *q = tmp;
}

void RandomSort(int *nArr, int nLen) {
    srand(time(NULL));
    for(int i = 0; i < nLen; ++i) {
        int nIndex = rand() % nLen;
        Swape(&nArr[i], &nArr[nIndex]);
        //Sleep(2000);                       //等待2s，更新随机种子
    }
}

void InitArr(int *nArr, int nLen) {     //初始化数组
    srand(time(NULL));
    for(int i = 0; i < nLen; ++i) {
        //nArr[i] = rand() % 100;
        nArr[i] = i;
    }
}

void PrintArr(int *nArr, int nLen) {   //打印数组
    for(int i = 0; i < nLen; ++i) {
        cout << nArr[i] << " ";
    }
    cout << endl;
}

//返回父节点下标
int Parent(int i) {
    return (i - 1) / 2;
}

//返回i左节点下标
int LeftChild(int i) {
    return 2 * i + 1;
}

//返回i右节点下标
int RightChild(int i) {
    return 2 * i + 2;
}

//最大堆化，保证每个父节点都比子节点大
void MaxHeapify(int *nArr, int nLen, int i) {
    int LC = LeftChild(i);
    int RC = RightChild(i);
    int nMaxPos;
    if(LC < nLen && nArr[LC] > nArr[i]) {
        nMaxPos = LC;
    } else {
        nMaxPos = i;
    }
    if(RC < nLen && nArr[RC] > nArr[nMaxPos]) {
        nMaxPos = RC;
    }

    if(nMaxPos != i) {
        Swape(&nArr[nMaxPos], &nArr[i]);
        MaxHeapify(nArr, nLen, nMaxPos);
    }
}

//将最大值移动到树的根节点，即数组头
void BuildMaxHeap(int *nArr, int nLen) {
    for(int i = Parent(nLen - 1); i >= 0; --i) {
        MaxHeapify(nArr, nLen, i);
    }
}

//最大堆排序
void HeapSort(int *nArr, int nLen) {
    BuildMaxHeap(nArr, nLen);                //将最大值移动至堆顶
    for(int i = nLen - 1; i > 0; --i) {
        Swape(&nArr[i], &nArr[0]);           //将堆顶的最大值放在数组最末尾nArr[nLen - 1]处
        --nLen;                              //在堆中去除末尾元素（因为已经排好序，最后一位是最大值）
        MaxHeapify(nArr, nLen, 0);           //从堆顶开始，将刚刚交换上来的nArr[i]往下移动，直至满足其父节点大于其本身的值
    }
}

int HeadQueue() {                  //取队头元素
    if(Arr == nullptr || Len == 0) {
        cout << "queue empty" << endl;
        return -1;
    }
    return Arr[0];
}

int PopQueue() {                    //出队
    if(Arr == nullptr || Len == 0) {
        cout << "queue empty" << endl;
        return -1;
    }
    int res = Arr[0];
    Swape(&Arr[Len - 1], &Arr[0]);
    --Len;
    BuildMaxHeap(Arr, Len);
    return res;
}

void PushQueue(int element) {      //入队
    ++Len;
    Arr[Len - 1] = element;
    BuildMaxHeap(Arr, Len);
}




int main() {
    Len = 0;

//    InitArr(nArr, Len);
//    RandomSort(nArr, Len);
//    PrintArr(Arr, Len);
//    cout << endl;

    //HeapSort(nArr, Len);
    cout << "push 5" << endl;
    PushQueue(5);
    cout << "push 9" << endl;
    PushQueue(9);
    cout << "push 3" << endl;
    PushQueue(3);
    cout << "push 15" << endl;
    PushQueue(15);
    cout << "push -4" << endl;
    PushQueue(-4);

    cout << "HeadQueue is " << HeadQueue() << endl;

    cout << "now queue is " << endl;
    PrintArr(Arr, Len);

    cout << "pop " << PopQueue() << endl;
    cout << "pop " << PopQueue() << endl;
    cout << "pop " << PopQueue() << endl;

    cout << "push 20" << endl;
    PushQueue(20);
    cout << "push 6" << endl;
    PushQueue(6);

    cout << "now queue is " << endl;
    PrintArr(Arr, Len);

    cout << "pop " << PopQueue() << endl;
    cout << "pop " << PopQueue() << endl;

    cout << "HeadQueue is " << HeadQueue() << endl;

    cout << "now queue is " << endl;
    PrintArr(Arr, Len);
    cout << endl;

    return 0;
}

3.运行结果

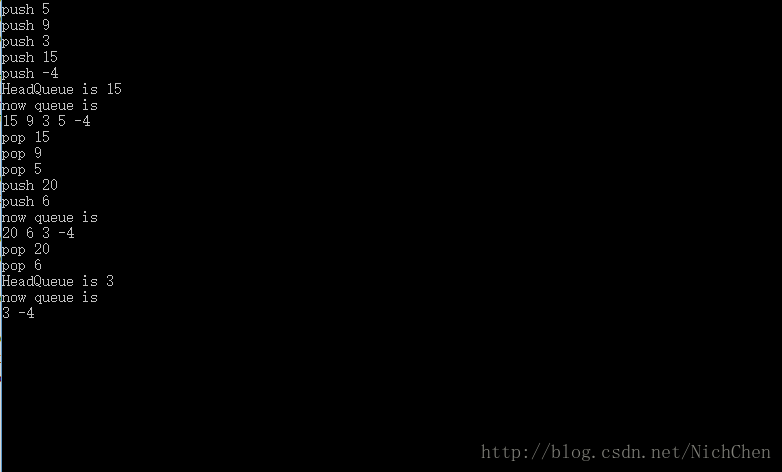
4.总结
需要注意的是，堆排序与二叉搜索树不同，二叉堆只保证了父节点大于子节点，因此在上面输出结果中，Arr数组并不能保证是降序排列的，但可以确保堆顶元素为队内最大值，即可以实现优先队列。出于性能考虑，优先队列用堆来实现，具有O(log n)时间复杂度的插入和提取元素性能，O(n)的初始化构造的时间复杂度。如果使用自平衡二叉查找树，插入与删除的时间复杂度为O(log n)，构造二叉树的时间复杂度为O(n log n)。